Глава 1

сторону AC в точке F, а хорда DE проходит через точку F, DF = 8 см и FE = 12 см. Вычислите длину стороны AC .

35. Стороны SO и SF угла OSF пересекают окружность соответ­ственно в точках A, B и C, D. Градусные меры дуг AC , CD, DB и BA в указанном порядке находятся в отношении 4 : 6 : 10 : 16. Вычислите градусную меру угла OSF.

36. Через точку S внутри окружности проведены две прямые l₁ и l₂, которые пересекают окружность соответственно в точках C, D и A, B. Градусные меры дуг AC , CB, BD и DA в указанном порядке на­ходятся в отношении 2 : 4 : 6 : 8. Вычислите градусные меры углов с вершиной S.

Замечательные точки треугольника

Скачено с Образовательного

портала www.adu.by

40

Глава 1

Вписанные и описанные многоугольники

41

§ 3. Замечательные точки треугольника

Ранее мы уже отмечали следующие свойства: медианы треуголь­ника пересекаются в одной точке; биссектрисы треугольника пересекаются в одной точке; высоты треугольника или их продолжения пересекаются в одной точке.

Теорема о свойстве точки пересечения медиан была доказана в девятом классе. Сейчас докажем теоремы о свойствах биссектрис и высот треугольника.

1. Теорема о точке пересечения биссектрис треугольника. Пред­варительно докажем одно свойство биссектрисы угла.

Те о р е м а 1 (о свойстве биссектрисы угла). Каждая точка биссектрисы угла, меньше развернутого, равноудалена от его сто­рон. Каждая точка указанного угла, равноудаленная от его сторон, лежит на биссектрисе этого угла.

а)

б)

Рис. 36

Д о к а з а т е л ь с т в о.

I. Докажем, что каждая точка биссектрисы угла, который меньше развернутого, равноудалена от его сторон.

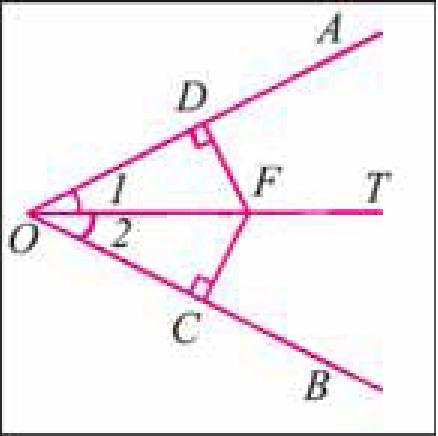
1) Пусть ОТ — биссектриса ∠ АО В , т. е. ∠ 1 = ∠ 2 и F — произ­вольная точка биссектрисы. Проведем перпендикуляры FC и FD к пря­мым BO и AO соответственно и докажем, что FC = FD (рис. 36, а).

2) Рассмотрим прямоугольные треугольники OFD и OFC. Эти треугольники равны по гипотенузе и острому углу (OF — общая гипотенуза, ∠ 1 = ∠ 2).

3) Из равенства треугольников OFD и OFC следует, что FC = FD. Что и требовалось доказать.

Скачено с Образовательного

II. Докажем, что если точка равноудалена от сторон угла меньше развернутого, то она лежит на его биссектрисе.

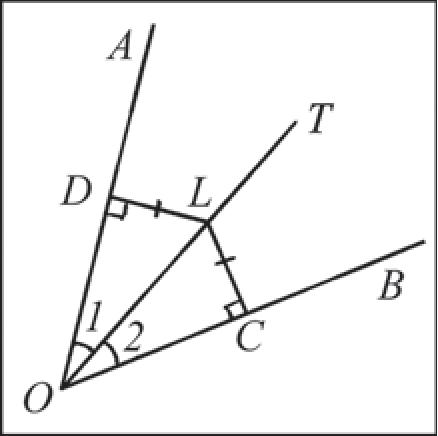
1. Пусть точка L равноудалена от сторон угла AO B , т. е. перпен­дикуляры LD и LC, проведенные к сторонам угла, равны. Докажем, что OL — биссектриса угла AO B (рис. 36, б).

2. Рассмотрим прямоугольные треугольники ODL и OCL. Эти треугольники равны по гипотенузе и катету (OL — общая гипотенуза, LD = LC).

3. Из равенства треугольников ODL и OCL следует, что ∠ 1 = ∠ 2, т. е. OL — биссектриса угла AO B . Что и требовалось доказать.

Те о р е м а 2 (о точке пересечения биссектрис). Биссектрисы треугольника пересекаются в одной точке.

	.'{■.л^Л'І'^РДі'іг
	Щ\иФ
	^^^щ^^У&
А ':	Щ^::ВуЕЩ:: С

Доказательство.

1) Пусть AA₁, BB₁ и CC₁ — биссектрисы треугольника ABC. Докажем, что они пересе­ каются в одной точке (рис. 37).

Обозначим буквой O точку пересечения биссектрис AA₁ и BB₁. Проведем из точки O перпендикуляры OF, OT и OE соответственно к прямым AB, BC и AC .

Рис. 37

2. По теореме о свойстве биссектрисы угла выполняются равенства OE = OF и OF = OT. Отсюда следует, что OE = OT.

3. Равенство OE = OT означает, что точка O равноудалена от сторон угла AC B . Следовательно, по теореме о свойстве биссектрисы угла следует, что точка O лежит на биссектрисе угла AC B . Иначе говоря, биссектриса CC₁ проходит через точку O. Таким образом, все три бис­сектрисы AA₁, BB₁ и CC₁ треугольника AC B пересекаются в точке O.

Теорема доказана.

2. Теорема о точке пересечения прямых, содержащих высоты тре­угольника. Ранее было введено понятие серединного перпендикуляра к отрезку и доказана теорема о серединном перпендикуляре: каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. И обратно: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Воспользуемся указанными свойствами для доказательства сле­дующей теоремы.

портала www.adu.by

42