Глава 1 вписанные и описанные многоугольники

§1. Взаимное расположение прямой

И окружности. Касательная к окружности

1. Взаимное расположение прямой и окружности. Рассмотрим вопрос о взаимном расположении прямой и окружности. Ранее уже отмечалось, что возможны три случая взаимного расположения прямой и окружности:

1. прямая имеет только две общие точки с окружностью;

2. прямая имеет только одну общую точку с окружностью;

3. прямая не имеет общих точек с окружностью.

Если прямая имеет две общие точки с окружностью, то она на­зывается секущей.

Взаимное расположение окружности со (О; R) с центром в точке О радиуса R и прямой / характеризуется соотношением между рас­стоянием d (0, /) от центра О окружности до прямой / и радиусом R окружности. Покажем это.

1) Прямая I имеет только две общие точки с окружностью, если расстояние от центра окружности до прямой I меньше радиуса окружности, т. е. если d (0, /) < R (рис. 1).

Пусть прямая / не проходит через центр О окружности и расстояние d (О, l) = m < R. Обозначим OF (F є /) пер­пендикуляр, проведенный из точки О к пря­мой /, тогда OF = т. Пусть точки А и В — точ­ки прямой / такие, что FA = FB = \JR² —mi². Докажем, что точки А и В принадлежат окружности.

Рис. 1

Действительно, так как по те­ореме Пифагора ОА = y/OF² +FA² = = уіт² + (R² -m²) = R и OB = y/OF² + FB² =

= ■yjm² +(R² -m²) = R, то OA = OB = R. Таким образом, точки А и В — общие точки прямой и окружности. Докажем, что других общих точек прямая / и окружность со (О; R) не имеют. Предположим, что существует еще одна точка X — общая

портала www.adu.by

8

Глава 1

Вписанные и описанные многоугольники

9

для окружности и прямой. Тогда центр окружности О равноудален от точек Л, В и X, а значит, он лежит на серединных перпендикулярах I₁ и 4 к отрезкам АВ и ВХ, т. е. О — точка пересечения серединных перпендикуляров 1₁ и /₂. Но так как 1₁ _1_ / и /₂ _1_ /, то ^ || /₂. Получили противоречие. Значит, наше предположение не верно и других общих точек прямой и окружности нет.

Если прямая / проходит через центр О окружности, т. е. d (О, I) = 0, то она пересекает окружность в двух точках, которые являются концами диаметра, лежащего на этой прямой.

2) Прямая I имеет только одну общую точку с окружностью, если расстояние от центра окружности до прямой I равно ра­ диусу окружности: d (0, l) = R.

Рис. 2

Пусть расстояние от центра окружности до прямой / равно ра­диусу окружности, а точка F — основание перпендикуляра, проведенного из центра окружности к прямой / (рис. 2). Тогда OF = R, а значит, точка Улежит на окружности. Дру гих общих точек прямая и окружность не имеют. Действительно, для любой точки X прямой /, не совпадающей с точкой F, выполняется условие ОХ > OF = R, так как наклонная ОХ больше перпендикуляра OF. Следовательно, точка X не лежит на окружности.

3) Прямая I не имеет общих точек с окружностью, если расстояние от центра О окружности до прямой I больше ра­ диуса окружности: d (0, /) > R.

Пусть расстояние от центра О окруж­ ности до прямой / больше радиуса R. Обозначим буквой/⁷основание перпендику­ ляра, проведенного из центра О окружности к прямой / (рис. 3). Тогда OF = d (О, 1) > R. Для любой точки X прямой выполняется условие ОХ > OF > R, следовательно, точка X не лежит на окружности. Таким образом, в случае d (0, /) > R прямая и окружность Рис. 3 не имеют общих точек.

2. Касательная к окружности. Рассмотрим случай, когда прямая и окружность имеют единственную общую точку. Прямая, имеющая единственную общую точку с окружностью, имеет специальное на­звание — касательная.

Определение. Касательной к окружности называется прямая, которая имеет с окружностью только одну общую точку.

Единственная общая точка прямой и окружности называется точкой касания прямой и окружности.

Если прямая l имеет единственную общую точку A с окружностью, то говорят, что прямая l касается окружности в точке A.

Те о р е м а (свойство касательной). Касательная к окруж­ности перпендикулярна ра диусу этой окружности, проведен ному в точку касания.

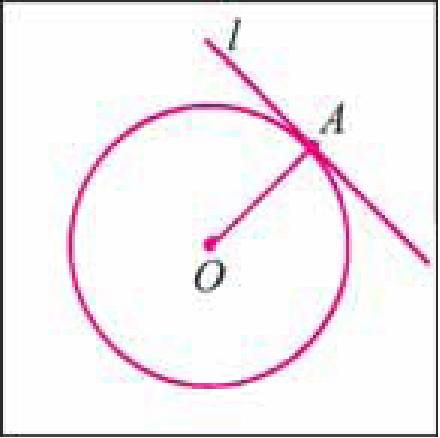
Доказательство.

1. Пусть прямая l касается окружности ω (O; R) в точке A (рис. 4). Докажем, что l ⊥ OA .

2. Предположим, что это не так. Тогда радиус OA является наклонной к прямой l. Перпендикуляр, проведенный из точки O к прямой l, меньше наклонной OA , следова­тельно, расстояние от центра окружности ^{Рис. 4} до прямой меньше радиуса. Значит, прямая и окружность имеют две общие точки, что противоречит условию. Таким образом, прямая l перпендикулярна радиусу OA .

Теорема доказана.

Рассмотрим следствия из данной теоремы.

Пусть через точку A проведены две прямые, касающиеся окружнос­ти ω (O; R) в точках C и B. Тогда отрезки AB и AC называются отрезками касательных, проведенными из точки A (рис. 5).

С л е д с т в и е 1. Отрезки касательных к окружности, проведенные из одной точки, равны.

Доказательство. 1) Пусть AB и AC — отрезки касатель­ ных, проведенные из точки A (см. рис. 5). _{Рис. 5}

Скачено с Образовательного портала www.adu.by

10