Глава 1

18. 

    Постройте прямоугольный треугольник по катету а и сумме s другого катета и гипотенузы.

19. Высоты CF и AT остроугольного треугольника ABC пересека­ются в точке О. Докажите, что Z АВО = Z АСО.

20. Высоты AF и ВТ, проведенные к боковым сторонам равнобед­ренного треугольника ABC, пересекаются в точке О и Е= СО П АВ (рис. 43, а). Докажите, что отрезок СЕ — медиана треуголь­ника ABC.

21. Высоты AF и СТ остроугольного треугольника ABC пересека­ются в точке О (рис. 43, б). Известно, что AT : FC = 1 : 2. Вычислите длину отрезка ОС, если АО = 4 см.

а)

б)

Рис. 43

22. Высоты AF и CT остроугольного треугольника ABC пересекают­ся в точке O. Вычислите длину высоты треугольника AO C , проведенной из вершины O, если AO = BF = 8 см, OF = 6 см.

Вписанные и описанные треугольники

Скачено с Образовательного портала www.adu.by

48

Глава 1

Вписанные и описанные многоугольники

49

§ 4. Вписанные и описанные треугольники

1. Окружность, вписанная в треугольник. Рассмотрим понятия окружности, вписанной в треугольник.

О п р е д е л е н и е. Окружность называется вписанной в тре­угольник, если она касается всех сторон треугольника. В этом случае треугольник называется описанным около окружности.

Например, на рисунке 44, а изображена окружность, вписанная в треугольник ABC. Окружность, которая изображена на рисунке 44, б, не является вписанной в треугольник ABC, так как она не касается стороны BC.

а)

б)

Рис. 44

Следующая теорема дает ответ на вопрос о существовании окружности, вписанной в треугольник.

Те о р е м а (о существовании окружности, вписанной в треугольник). В любой треугольник можно вписать единственную окружность.

Д о к а з а т е л ь с т в о.

I. Докажем, что в треугольник можно вписать окружность.

1. Пусть ABC — произвольный тре­угольник, O — точка пересечения его бис­сектрис (рис. 45).

2. Проведем из точки O перпендикуля­ры OK, OE и O T к сторонам AB, BC и A C соответственно.

3. По теореме о биссектрисе угла точка O равноудалена от сторон треугольника,

_{Рис. 45} следовательно, OK = OE = OT. Таким обра-

Скачено с Образовательного

зом, окружность с центром в точке O и радиусом, равным отрезку OK, проходит через точки K, E и T.

4) Стороны AB, BC и A C треугольника касаются этой окружности в точках K, E и T, так как они перпендикулярны соответственно радиу­сам OK, OE и OT. Следовательно, окружность с центром в точке O радиуса OK является вписанной в треугольник ABC. Существование вписанной окружности доказано.

II. Докажем, что такая окружность единственная.

Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из окружностей равноудален от сторон треуголь­ника, а следовательно, совпадает с точкой O пересечения биссектрис треугольника; ее радиус равен расстоянию от точки O до сторон тре­угольника. Таким образом, эти окружности совпадают.

Теорема доказана.

2. Окружность, описанная около треугольника. Рассмотрим понятие окружности, описанной около треугольника.

О п р е д е л е н и е. Окружность называется описанной около треугольника, если все его вершины лежат на этой окружности. В этом случае треугольник называется вписанным в окружность.

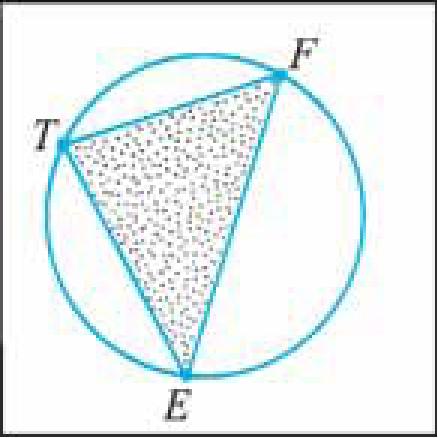
Например, на рисунке 46, а изображена окружность, которая является описанной около треугольника TFE. Окружность, которая изображена на рисунке 46, б, не является описанной около треуголь­ника ABC, так как вершина C не лежит на окружности.

б)

а)

Рис. 46

Докажем теорему о существовании описанной около треугольника окружности.

портала www.adu.by

50