Глава 3

40. Окружность с центром O на гипотенузе AC прямоугольного треугольника касается его катетов AB и BC в точках F и E соответ­ственно. Вычислите длины окружностей, построенных на отрезках AO и CO как на диаметрах, если AB = 3 см и BC = 4 см.

41. В прямоугольный треугольник вписана полуокружность так, что ее диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки 15 см и 20 см. Вычислите длину полуокружности.

42. В равносторонний треугольник вписана окружность. Окружность радиуса r касается этой окружности и сторон треуголь­ ника. Найдите радиус окружности, вписанной в треугольник.

43. Через точку S к окружности проведены прямые l₁ и l₂, которые касаются окружности в точках A и B. Меньшая окружность касается данных прямых и большей окружности в точке F. Найдите длину мень­шей окружности, если дуга AFB равна 120°, а ее длина равна m.

44. Окружность вписана в равнобедренную трапецию, а ее бо­ковая сторона точкой касания делится на отрезки длиной 4 см и 9 см. Вычислите длину окружности, вписанной в трапецию.

Скачено с Образовательного портала www.adu.by

124

Глава 3

Длина окружности и площадь круга

125

§ 3. Площадь круга. Площадь сектора

а) б) в)

Рис. 100

1. Площадь круга. Рассмотрим вопрос о вычислении площади круга. Пусть в окружность, ограничивающую круг, вписан правильный n-уголь­ник. Если число n сторон правильного n-угольника, вписанного в окруж­ность, неограниченно возрастает, то многоугольник все меньше и меньше отличается от круга (рис. 100, а, б). Из результатов, доказываемых в вузовском курсе математического анализа, следует, что существует число, к которому стремятся площади S_n правильных n-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется площадью круга. Таким образом, за площадь круга принимается число, к которому стремятся площади вписанных в окружность, ограничивающую этот круг, правильных n-угольни­ков при неограниченном увеличении числа их сторон.

180° 180°

стремится к нулю, а значит, cos стремится к единице, т. е.

я я

г_п стремится к R. Кроме того, периметр Р_п стремится к длине окруж­ности, равной 2%R, а площадь S_n стремится к площади S круга. Таким

с 1 о D п2 Т

образом, площадь круга д = — • z%R ■ R = tzR . еорема доказана.

2

2. Площадь сектора. Рассмотрим вопрос о вычислении площади части круга, которая называется сектором.

Определение. Сектором называется часть круга, ограни­ченная дугой окружности и двумя радиусами, соединяющими кон­цы дуги с центром круга.

Дуга окружности, ограничивающая сектор, называется дугой сектора. Например, на рисунке 101, а изображены два сектора, ду­гами которых служат дуги АТВ и AFB. На рисунке 101, б изображе­ны круг, который касается всех сторон треугольника, и два сектора, ограниченные радиусами, проведенными в точки касания, и соот­ветствующими дугами окружности.

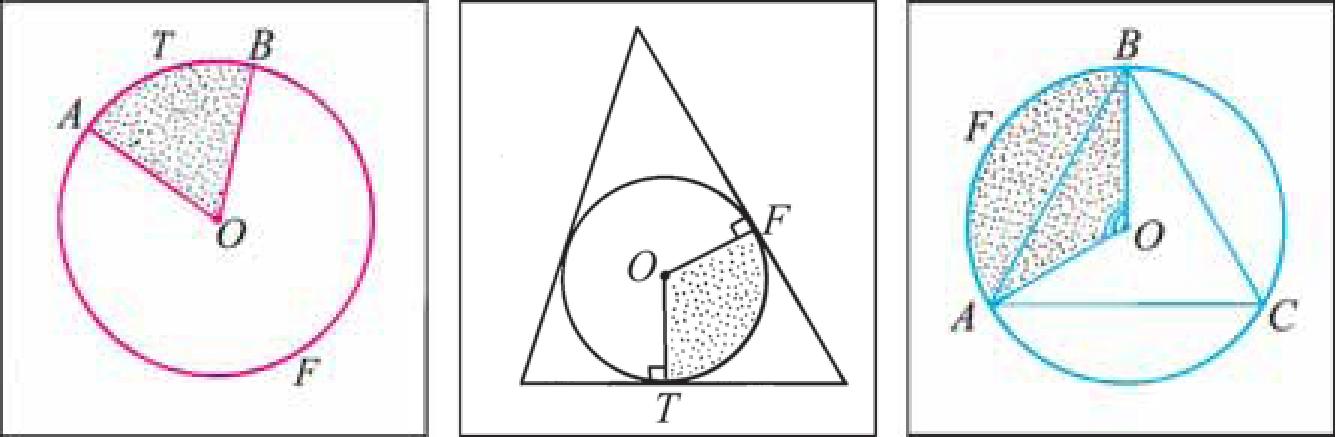
Теперь докажем следующую теорему.

Теорема (о площади круга). Площадь S круга радиуса R вычисляется по формуле S = tzR².

1) Пусть дан круг радиуса R и А₁А₂- А_п_₁А_п — правильный п-угольник, вписанный в окружность, которая ограничивает этот круг. На рисунке 100, в дано изображение для случая п = 6. Если Р_п — периметр вписанного многоугольника, а г_п — радиус вписанной

в него окружности, то S_n — площадь этого многоугольника находится

_ 1 _

по формуле Ъ_п = nS_A0, = —Р_п ■ г_п.

2

2) При неограниченном увеличении числа п сторон п-угольника

радиус г_п вписанной окружности стремится к R. Действительно, так как

180° г_п = Rcos , то при неограниченном увеличении числа сторон п число

я

Скачено с Образова

а) б) в)

Рис. 101

Выведем формулу для вычисления площади S сектора радиусом R, дуга которого имеет градусную меру а. Площадь круга радиусом R равна %R². Следовательно, площадь сектора, ограниченного дугой

О Я/?² _с

в 1 , равна . Значит, площадь Ь сектора, ограниченного дугой

360° ₂

в а градусов, выражается формулой S_сект = • а.

360°

Например, если ABC — равносторонний треугольник, вписанный в круг радиуса R, а точка О — его центр, тогда площадь сектора,

Г Г\ /I CD TlR 1 ОАО TlR

ограниченного радиусами UA, UB и дугой АгВ, равна • lzU =

360° 3

(рис. 101, в).

портала www.adu.by

126