Глава 4

Задачи для повторения

157

3. Произвольный треугольник и окружность

46. В остроугольном треугольнике ABC проведены высоты AF и СТ. Найдите радиус окружности, описанной около треугольника BFT, если ZABC = 60° и АС = b (рис. 118, а, б).

Д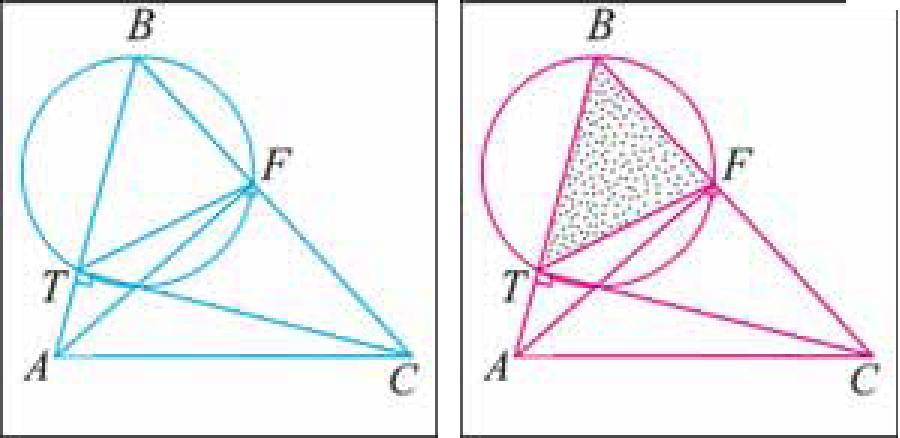 ано: ААВС, Z ABC = 60°, АС = b, AF_L.BC, СТ LAB.

Н а й т и. i\gpj.

а) б)

Рис. 118

Решение.

Воспользуемся теоремой синусов и тем, что треугольник

ABC подобен треугольнику FBT.

1) В треугольнике FBT по теореме синусов выполняется равенство

TF о г> г> TF TF

= z Л>_В7-- Следовательно, Л^ = = -_.

sin60° 2sin60° v3

2) Рассмотрим треугольники ЛВС и /ТС. Эти треугольники по-

добны. Действительно,

cos B. Следовательно,

BF „ ВГ

= cose и ВА ВС

BF ВТ „ г-тто

циентом подобия cos B = cos 60°

= = cos В, т. е. треугольники ABC и г/и подобны с коэффи-ВА ВС

3) Из подобия треугольников ЛВС и /ТС следует, что TF = b cos В

6 ТУ⁷ b [7ї 6л/3

6

TF b

Таким образом, R_FBT

л/3

= = ;

2

\[3 2

6V3 6

О т в е т:

47. В остроугольном треугольнике ABC отрезки АР и СТ — высо­ты. Известно, что площадь треугольника ABC равна 18 см², а длины отрезков ТР и АС равны 2v2 см и 6v2 см соответственно. Вычислите площадь треугольника ВТР.

48. Отрезки АЕ и СК— высоты остроугольного треугольника ЛВС Вычислите диаметр окружности, описанной около четырехугольника

Скачено с Образовательного

АКЕС, если известно, что периметры треугольников ABC и В/Жравны 15 см и 9 см соответственно, а радиус окружности, описанной около треугольника ВЕК, равен 1,8 см.

49. На стороне ВС треугольника ABC как на диаметре построена окружность, которая пересекает стороны АВ и АС соответственно в точках F и Т. Найдите площадь треугольника AFT, если площадь треугольника ABC равна S, а угол ВАС равен 30°.

50. Отрезок АВ является диаметром круга, а точка С лежит вне этого круга. Отрезки АС и BD пересекают граничную окружность в точках D и F соответственно. Вычислите градусную меру угла CBD, если площадь треугольника ABC в четыре раза больше площади треугольника CDF.

51. Окружность вписана в треугольник, периметр которого равен 20 см. Отрезок касательной, проведенной к окружности параллельно основанию, расположенный между сторонами треугольника, равен 2,4 см. Вычислите длину основания треугольника.

52. Окружность, вписанная в треугольник ABC, касается сторо­ны АС в точке F. Докажите, что AF = р — а, где р — полупериметр треугольника ABC, ВС = а.

53. В параллелограмме ABCD длины сторон АВ и ВС равны соответственно 4 см и 10 см. В треугольники ABD и BCD вписаны окружности, касающиеся диагонали BD в точках/⁷ и Г соответственно. Вычислите длину отрезка FT.

54. Периметр треугольника равен 2р, сторона АС = b, Z ABC = р (0 < р < 90°). Вписанная в треугольник окружность касается сто­роны ВС в точке К- Найдите площадь треугольника ВОК, где точка О — центр вписанной окружности.

55. В треугольнике ABC биссектрисы BF и AT пересекаются в точке О. Вычислите длину стороны АС, если АВ = 24 см, АО : ОТ = 3 : 2 и AF : FC = 6 : 7.

56. Докажите, что в произвольном треугольнике ABC справедлива формула ll = ас — а₁с₁, где 1_Ь — длина биссектрисы BD угла В, а и с — длины сторон В А и ВС соответственно, а₁ и с₁ — длины отрез­ков, на которые биссектриса угла В делит сторону АС, прилежащих к стороне ВС и ВА соответственно (рис. 119, а).

портала www.adu.by

158