Глава 3

Длина окружности и площадь круга

119

а) б)

Рис. 97

10. Точки Т, Е, /Си Е лежат соответственно на сторонах АВ, ВС, CD и AD квадрата ABCD. Вычислите длину окружности, вписанной в четырехугольник TFKE, если АВ = 3 см и АЕ =ТВ = ЕС = KD = 1 см (рис. 97, б).

11. Длина окружности, описанной около прямоугольника, равна 20π см. Вычислите периметр прямоугольника, если его диагональ образует со стороной угол 30°.

12. Площадь прямоугольника ABCD равна 12 см², а его пери­метр — 14 см. Вычислите длину окружности, описанной около тре­угольника ABC.

13. Отрезок BE — перпендикуляр, проведенный из вершины В прямоугольника ABCD, к его диагонали АС. Вычислите длину окружности, описанной около прямоугольника, если BE = 6 см и АЕ= 4 см.

14. Вычислите длину окружности, описанной около прямоуголь­ного треугольника, если его площадь равна 48 см², а длина одного из катетов — 6 см.

15. Длина окружности, описанной около прямоугольного тре­угольника, равна 26π см, а длина одного из его катетов равна 10 см. Вычислите площадь треугольника.

16. Вычислите длину окружности, вписанной в прямоугольный треугольник, длины катетов которого равны 6 см и 8 см.

17. Одна из диагоналей ромба равна его стороне. Вычислите длину окружности, вписанной в ромб, если его периметр равен 40 см.

Скачено с Образова

18. Длина окружности, вписанной в ромб, равна 2π\/3 см. Вычислите площадь этого ромба, если его сторона равна диагонали.

19. Острый угол ромба ABCD равен 60°. Точки Т, Е, /Си Р — се­редины сторон АВ, ВС, CD и AD соответственно. Найдите длину окружности, описанной около четырехугольника ТЕКР, если сторона ромба равна а.

20. Длина стороны основания равнобедренного треугольника равна 16 см, а угол при его вершине равен 150°. Вычислите длину окружности, описанной около этого треугольника.

21. Угол при основании равнобедренного треугольника равен 75°, а длина его основания равна 10 см. Вычислите длину окружности, описанной около треугольника.

18. Длина окружности, описанной около равнобедренного тре-

25 угольника, равна —π см. Вычислите синус угла при основании тре­угольника, если длина его боковой стороны равна 5 см.

23. Длина окружности, описанной около равнобедренного тре­ угольника ABC, равна 25π см, отрезок BE — диаметр окружности. Вычислите длину хорды ЕС, если высота, проведенная к основанию АС, равна 16 см (рис. 98, а).

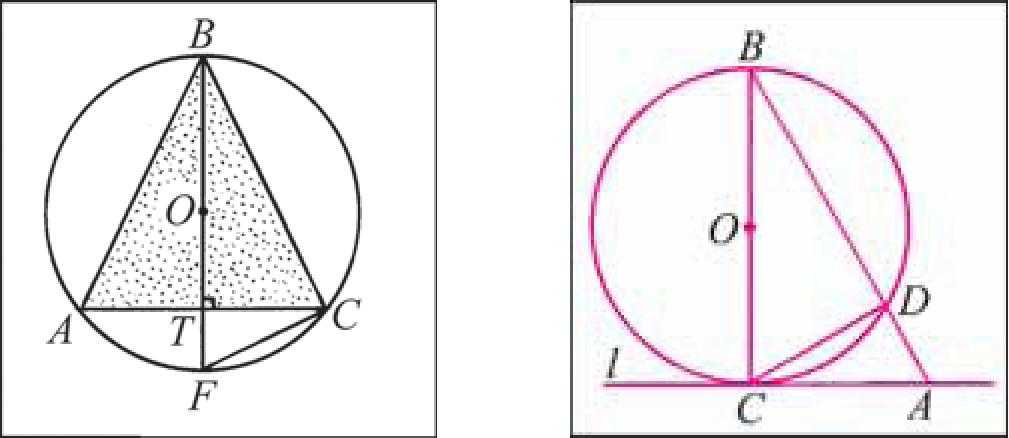
а) б)

Рис. 98

24. Отрезок ВС является диаметром окружности, а в точке С проведена касательная / к окружности, и точка А Є / (рис. 98, б). Отрезок АВ пересекает окружность в точке D так, что AD : DB = 1 : 3. Вычислите длину окружности, если длина хорды CD = 3 см.

портала www.adu.by

120