2. Теорема об отношении длины окружности к ее диаметру.

Докажем теорему, которая характеризует отношение длины окруж­ности к ее диаметру.

Те о р е м а ( об отношении длины окружности к ее диаметру). Отношение длины окружности к ее диаметру есть число постоянное для всех окружностей.

Скачено с Образовательного портала www.adu.by

114

Глава 3

Длина окружности и площадь круга

115

Дано: со (О; 7?), ю! (0[; 7?!) — окруж­ности, С, С₁ — длины окружностей. Доказать: С С[ 2R 2R

Скачено с Образовательного портала www.adu.by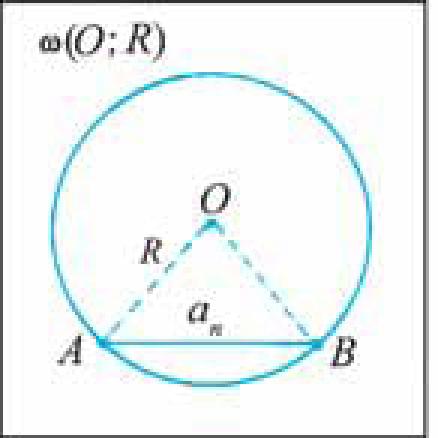

"МО,; *,) ( *Д	*я,
л^-^

б)

а)

Рис. 94

Доказательство.

180°

180°

1. Впишем в каждую из окружностей правильные п-угольники. Пусть а_п, а'_п — стороны этих многоугольников, Р_п, Р'_п — соответ­ственно их периметры (рис. 94, а, б).

2. Теперь воспользуемся формулой, по которой находится сто­рона правильного п-угольника через радиус описанной окружности. Учитывая эту формулу (§ 1, п. 4, гл. 3), можем записать равенства

Р_п = п ■ а = п ■ 2Rsm и Р'_п = п ■ а'_п = п ■ 2R_l sin

п

Следовательно,

п

верно равенство

(1).

2R Р' 2R,

п 1

3) Это равенство верно при любом значении п. Будем неограни­ченно увеличивать число п, тогда периметр Р_п первого многоугольни­ка стремится к длине С первой окружности, а периметр Р'_п второго

многоугольника стремится к длине С_х другой окружности, т. е.

5l

р'

стремится к ^C .

2R 2R

C₁

с

с

Отсюда следует, что

4) Таким образом, ^C

2R 2R

Значит, отношение длины окружности к ее диаметру одно и то же для всех окружностей.

Теорема доказана.

Число, равное отношению длины окружности к ее диа­метру, обозначается строчной греческой буквой % (читается «пи»). Доказано, что число п — иррациональное, т. е. выражается бесконечной непериодической десятичной дробью. Приближенное значение числа п с точностью до восьми знаков после запятой такое:

% & 3,14159265. При решении задач в школьной практике пользуются приближенным значением числа п с точностью до сотых: п » 3,14.

с

3. Длина окружности. Длина дуги окружности. Для нахождения

п. Отсюда

формулы длины окружности воспользуемся равенством

2R

следует, что длина окружности радиуса R находится по формуле С = 2%R или по формуле С = %D, где D — диаметр окружности.

Теперь выведем формулу для вычисления длины / дуги, градусная мера которой равна а. Пусть данная дуга является дугой окружности радиуса R. Так как длина всей окружности равна 2%R, то длина дуги в

1 ° 2-kR %R

1 равна = . Так как градусная мера дуги равна а, то длина

360° 180° „

I этой дуги выражается: I = .

180°

Дано: ААВС, А В = ВС = С А = а, AF = FB, FeAB, ВТ= ТС, ТєВС, АК=КС, КєАС. Найти: длину окружности, впи­санной в AFTK

Задача 1. Точки F, ТиК — середины сторон равностороннего тре­угольника ABC. Найдите длину окружности, вписанной в треугольник FTK, если сторона треугольника ABC равна а.

		в
	FA	/Ту	¥
А	л	Ф	'\	V
		к

б)

а)

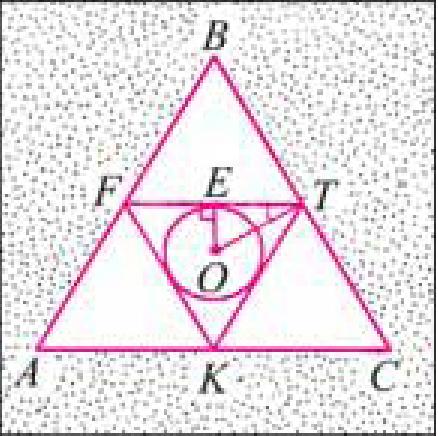
Рис. 95

Решение.

Для нахождения длины окружности можем воспользоваться формулой С = 2%г, где г — радиус окружности, вписанной в тре­угольник FTK- Для нахождения радиуса г воспользуемся тем, что треугольник FTK также является равносторонним.

1. Пусть точка О — центр окружности, вписанной в треугольник FTK, а E — точка касания окружности и стороны FT (рис. 95, а, б).

2. Треугольник FTK является равносторонним, так как FT = ТК= = KF = —АВ. Треугольник ТЕО — прямоугольный и Z EOT = 30°

116