Вопросы ко второй главе

1. Площадь треугольника ABC равна 3 см², а длины двух его сторон равны 2 см и 6 см. Верно ли, что угол между данными сторонами равен 60°?

1. Верно ли, что синус угла треугольника ABC можно найти по

формуле sin ос= —, где Ь — площадь треугольника, АВ= с, ab

АС= b, a — угол, лежащий против стороны ВС= а?

3. Два угла треугольника равны аир. Сторона, лежащая против

угла а, равна т. Верно ли, что сторона, лежащая против угла

_п msinB_ р, равна -?

sina

4. Радиус окружности, описанной около треугольника, равен /?, а один из его углов равен ср. Верно ли, что сторона, лежащая против угла ф, равна 2R s\r\ ср?

5. Градусная мера угла при вершине равнобедренного треугольника равна 120°, а длина боковой стороны равна а. Чему равен радиус окружности, описанной около данного треугольника?

6. Градусная мера угла при основании равнобедренного треугольника равна 15°, а радиус описанной окружности равен R. Найдите основание треугольника.

7. Чему равна площадь выпуклого четырехугольника, если его диагонали взаимно перпендикулярны и равны тип?

8. В равнобедренном треугольнике основание равно а, а боковая сторона равна р. Найдите медиану, проведенную к боковой стороне данного треугольника.

4. При каком условии площадь выпуклого четырехугольника равна

— тп, где тип — длины диагоналей четырехугольника?

2

Скачено с Образовательного портала www.adu.by

Правильные многоугольники.

Длина окружности и площадь круга.

Координатный метод

Правильные многоугольники

Скачено с Образовательного портала www.adu.by

Глава 3

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ.

ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА.

КООРДИНАТНЫЙ МЕТОД

§ 1. Правильные многоугольники

1. Правильный многоугольник. В предыдущих классах уже были изучены свойства равностороннего треугольника и квадрата. Каждая из этих фигур обладает тем свойством, что у них все углы и все стороны равны. Указанные геометрические фигуры служат примерами правильных многоугольников, свойства которых и рассматриваются в данном параграфе.

О п р е д е л е н и е. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

	„ '.' ■' -'-1
.= .,,-.. -■■	;■, Я ■;'■.;■;-.-.-■''■■
"^'■Jl'.-JV'-""'	.■/G;^V.-f-;v--- ■:■:.
ш^щ	/V:',,^
■■■?S--r'.:y2	-^
Й1	tea
	у y;
'Ш ^.-s':	ШШІ:

в)

а)

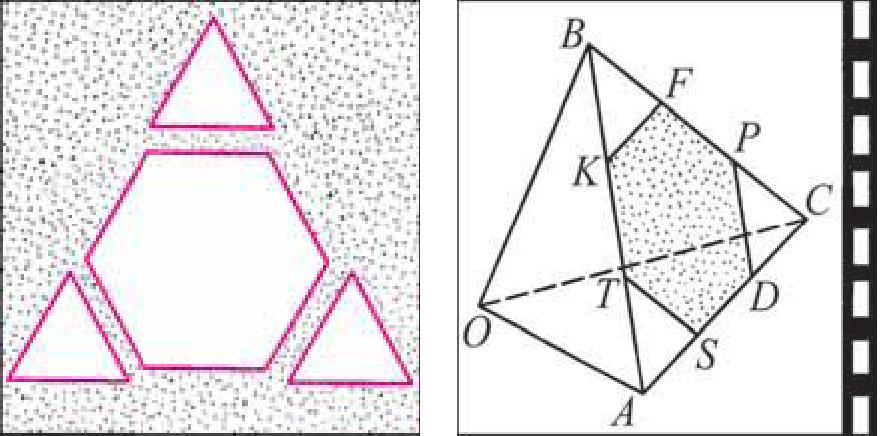
б) Рис. 81

Рассмотрим пример. Пусть ABC — равносторонний треугольник. Разделим каждую его сторону на три равные части, как показано на рисунке 81, а. Каждый из треугольников ATS, KBF и DPC является равносторонним. Отсюда следует, что Z1 =Z2 = Z3 = Z4 = Z5 = = Z 6 = 180° – 60° = 120°. Кроме того, ST = ТК= KF = FP = PD = DS. Таким образом, шестиугольник TKFPDS является правильным.

Модель этого правильного многоугольника получится, если от лис­та бумаги, имеющего форму равностороннего треугольника, отрезать равные части, имеющие форму равносторонних и равных между собой треугольников, как показано на рисунке 81, б.

Если треугольник ABC является гранью правильного тетраэдра ВОАС (правильный тетраэдр — треугольная пирамида, у которой все

Скачено с Образовательного

99