
- •В. В. Шлыков
- •Соотношения между сторонами и углами произвольного треугольника
- •Правильные многоугольники. Длина окружности и площадь круга. Координатный метод
- •Уважаемые друзья!
- •Глава 1 вписанные и описанные многоугольники
- •§1. Взаимное расположение прямой
- •И окружности. Касательная к окружности
- •Глава 1
- •Глава 1
- •12 Глава 1
- •14 Глава 1
- •Глава 1
- •Задачи к § 1
- •20 Глава 1
- •Глава 1
- •Глава 1
- •§ 2. Центральные и вписанные углы
- •Глава 1
- •Глава 1
- •Глава 1
- •3. Свойство пересекающихся хорд. Теорема о касательной и секущей.
- •Глава 1
- •Задачи к § 2
- •34 Глава 1
- •Глава 1
- •Глава 1
- •Глава 1
- •§ 3. Замечательные точки треугольника
- •Глава 1
- •Задачи к § 3
- •Глава 1
- •Глава 1
- •Глава 1
- •§ 4. Вписанные и описанные треугольники
- •Глава 1
- •Глава 1
- •Глава 1
- •56 Глава 1
- •Глава 1
- •Глава 1
- •§ 5. Вписанные и описанные четырехугольники
- •Глава 1
- •Глава 1
- •Задачи к § 5
- •Глава 1
- •Глава 1
- •Глава 1
- •Глава 1 Вопросы к первой главе
- •Соотношения между сторонами и углами произвольного треугольника Теорема синусов
- •2) Отсюда следует, что выполняются равенства: Глава 2
- •§ 1. Теорема синусов
- •Теорема косинусов. Формула Герона. Решение треугольников
- •§ 2. Теорема косинусов. Формула Герона. Решение треугольников
- •Задачи к § 2 I
- •Вопросы ко второй главе
- •Глава 3
- •§ 1. Правильные многоугольники
- •Правильные многоугольники
- •2. Окружность, описанная около правильного многоугольника.
- •Глава 3
- •Глава 3
- •4) Площадь s правильного п-угольника можем найти по
- •Глава 3
- •5) Радиус r вписанной окружности выражается через
- •Задачи к § 1
- •108 Глава 3
- •110 Глава 3
- •§ 2. Длина окружности
- •2. Теорема об отношении длины окружности к ее диаметру.
- •Глава 3
- •Глава 3
- •Задачи к § 2
- •Глава 3
- •Глава 3
- •Глава 3
- •Глава 3
- •§ 3. Площадь круга. Площадь сектора
- •Глава 3
- •Глава 3
- •Задачи к § 3
- •130 Глава 3
- •132 Глава 3
- •Глава 3
- •Глава 3
- •§ 4. Координатный метод
- •Глава 3
- •Глава 3
- •Глава 3
- •Задачи к § 4
- •Глава 3
- •Глава 3 Вопросы к третьей главе
- •Глава 4 задачи для повторения
- •§ 1. Треугольники и окружность
- •1. Прямоугольный треугольник и окружность
- •Задачи для повторения
- •Глава 4
- •Глава 4
- •2. Равнобедренный треугольник и окружность
- •Глава 4
- •Глава 4
- •3. Произвольный треугольник и окружность
- •Глава 4
- •Глава 4
- •§ 2. Четырехугольники и окружность
- •1. Произвольный четырехугольник и окружность
- •Глава 4
- •2. Трапеция и окружность
- •Глава 4
- •166 Глава 4
- •Глава 1
- •Глава 2 § 1
- •Глава 3 § 1
- •Глава 4 § 1
- •Значения тригонометрических функций
- •172 Приложение
- •220004, Минск, проспект Победителей, 11.
Глава 1
BD и AE — высоты равнобедренного треугольника ABC с основанием AC . Радиусы окружностей, вписанных в треугольники ABD и AEC, равны соответственно 10 см и 12см. Вычислите радиус окружности, вписанной в треугольник ABC.
Постройте прямоугольный треугольник по гипотенузе c и радиусу r вписанной окружности.
Постройте прямоугольный треугольник по гипотенузе c и медиане m, проведенной к катету.
Постройте прямоугольный треугольник по гипотенузе c и биссектрисе l прямого угла.
Вписанные и описанные четырехугольники
Скачено с Образовательного портала www.adu.by
60
Глава 1
Вписанные и описанные многоугольники
61
§ 5. Вписанные и описанные четырехугольники
1. Окружность, вписанная в четырехугольник. Определим понятие окружности, вписанной в четырехугольник.
О п р е д е л е н и е. Окружность называется вписанной в четырехугольник, если она касается всех сторон четырехугольника. В этом случае четырехугольник называется описанным около окружности.

Например, на рисунке 53, а изображен квадрат и вписанная в него окружность. Заметим, что не в любой четырехугольник можно вписать окружность. Например, в прямоугольник, не являющийся квадратом, нельзя вписать окружность. Существует окружность, которая касается трех сторон прямоугольника, и не существует окружности, касающейся всех четырех сторон прямоугольника — неквадрата (рис. 53, б).
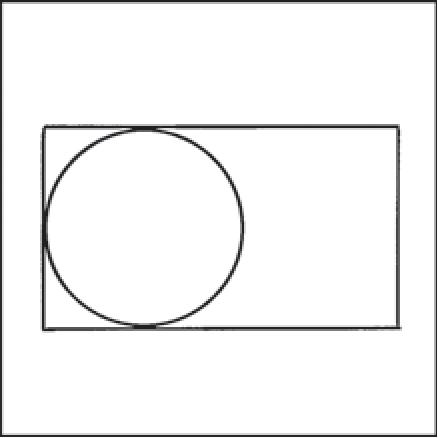
а)
б)
Рис. 53
Следующая теорема характеризует свойство четырехугольника, в который можно вписать окружность.

Те о р е м а 1 (о свойстве четырехугольника, в который можно вписать окружность). Если в четырехугольник можно вписать окружность, то суммы длин его противолежащих сторон равны.
Д о к а з а т е л ь с т в о.
1) Пусть в четырехугольник ABCD вписана окружность, которая касается его сторон в точках F, O, T и E (рис. 54).
Рис. 54
Докажем, что AB + CD = BC + AD.
Скачено с Образовательного
2) Та к как отрезки касательных к окружности, проведенные из одной точки, равны, то AF = AE = a, BF = BO = b, CO = CT = m, DT = DE = c.
3 ) Таким образом, A B + C D = (A F + F B ) + ( C T + DT ) = = a + b + c + m и BC + AD = (BO + OC) + (AE + ED) = a + b + + c + m. Отсюда следует, что AB + CD = BC + AD.
Теорема доказана.
Справедливо и обратное утверждение, которое отвечает на вопрос, при каком условии в четырехугольник можно вписать окружность.

[Те о р е м а 2 (условие, при котором в четырехугольник можно вписать окружность)]. Если в выпуклом четырехугольнике суммы длин противолежащих сторон равны, то в этот четырехугольник можно вписать окружность.

б)
а)
Рис. 55
Д о к а з а т е л ь с т в о.
1) Пусть ABCD — выпуклый четырехугольник, в котором АВ + CD = BC + AD. Докажем, что в этот четырехугольник можно вписать окружность.
Рассмотрим окружность, которая касается трех сторон: АВ, ВС и AD. Центр О этой окружности есть точка пересечения биссектрис углов СВА и BAD (рис. 55, а).
Докажем, что эта окружность вписана в четырехугольник, т. е. что она касается также и стороны CD. Предположим, что это не так. Тогда либо сторона CD не пересекает окружность, либо является секущей.
4) Пусть сторона CD не пересекает окружность (рис. 55, б). Проведем касательную DF, где F ^ BC. Так как ABFD — описанный четырехугольник, то верно равенство АВ + DF = AD + BF. Кроме
портала www.adu.by
62
