3. Свойство пересекающихся хорд. Теорема о касательной и секущей.

Теорема 3 (об отрезках пересекающихся хорд). Если две хорды окружности пересекаются, то произведение длин от­резков одной хорды равно произведению длин отрезков другой хорды.

В
С/0\
іВпЩк
А\. ^
^-—	**j5

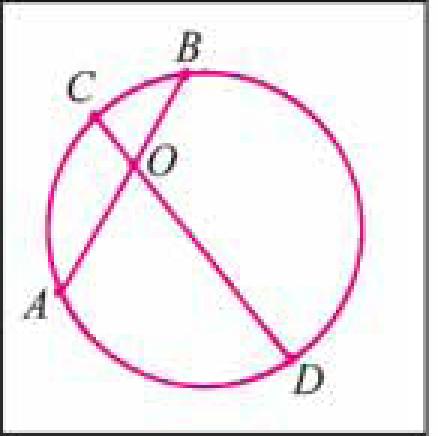
Дано: окружность, АВ, CD — хорды, О=АВП CD (рис. 28, а). Доказать: АО ■ ОВ = СО ■ OD.

а) б)

Рис. 28

Доказательство.

1. Проведем хорды АС и BD (рис. 28, б). Рассмотрим треугольники АОС и DOB.

2. Заметим, что Z 1 = Z 2, так как они вписанные и опираются на одну и ту же дугу СВ. Кроме того, Z 3 = Z 4, так как они опираются на одну и ту же дугу AD.

3. Треугольник АОС подобен треугольнику DOB по первому при­знаку подобия треугольников.

Скачено с Образовательного

4) Из подобия треугольников АОС и DOB следует, что — —. Значит, АО ■ ОВ = СО ■ OD.

Теорема доказана.

Пусть через точку S, лежащую вне окружности, проведена се­кущая, которая пересекает окружность в точках С и В и SC < SB. Тогда отрезок SB называется отрезком секущей, а отрезок SC — ее внешней частью (рис. 29, а).

Теорема 4 (об отрезках секущей и касательной). Если через точку, лежащую вне круга, ограниченного окруж­ностью, провести к этой окружности касательную и секущую, то квадрат длины отрезка касательной равен произведению длин отрезков секущей и ее внешней части.

Дано: со (О; R), SA — касательная, SB — секущая, SC — внешняя часть секущей (см. рис. 29, а). Доказать: SA² = SB ■ SC.

б)

а)

Рис. 29

Доказательство.

1. Проведем хорды АС и АВ (рис. 29, б).

2. По теореме о вписанном угле ZABC =yjAC. Кроме того, в

силу теоремы 2 имеем Z SAC = — kjAC. Значит, Z ABC = Z SAC.

2

3. Так как ZABC = Z SAC и Z 1 — общий угол треугольников ASB и CSA, то эти треугольники подобны.

3. Из подобия треугольников ASB и CSA следует, что выполняется

AS SB о „ „

равенство — = — или AS = SB ■ SL.

SC AS

Теорема доказана. Из данной теоремы получаем следствие.

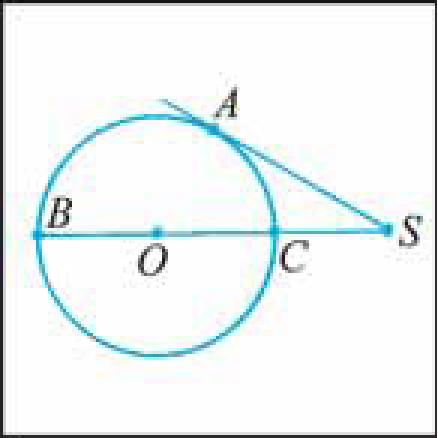
Следствие. Если из точки S к окружности проведены две секущие, пересекающие окружность соответственно в точках С„ В_х и С₂, В₂, тогда SB_X ■ SC_X = SB₂ ■ SC₂ (рис. 30, а).

портала www.adu.by

32

Глава 1

Вписанные и описанные многоугольники

33

Скачено с Образовательного портала www.adu.by

а)

б)

Рис. 30

Задача 1. Пусть через точку S проведена секущая, которая проходит через центр окружности со (О; R) и пересекает ее в точках С и В так, что SC : СВ = 1 : 2. Найти длину отрезка SA касательной (рис. 30, б).

Решение.

По теореме об отрезках секущей и касательной име­ем SA² = SC ■ SB. Так как SC : СВ = 1 : 2, СВ = 2R, SC = R и

SB = SC + CB = 3R, то SA² = SC ■ SB = 3R ■ R = 3R² и SA = ^/3R.

Ответ: V37?.

Задача 2. Внутри круга радиуса 7,5 см взята точка Р на расстоянии 6,5 см от его центра О. Через точку Р проведена хорда АВ, длина которой 9 см. Вычислите длины отрезков, на которые точка Р делит хорду АВ.

Дано: со (О; R), R = 7,5 см, Р є АВ, РО = 6,5 см, АВ = 9 см. Найти: ВР и АР.

а) б)

Рис. 31

Р е ш е н и е.

Воспользуемся теоремой об отрезках пересекающихся хорд. 1) Пусть C и D — точки пересечения прямой OP с граничной окружностью данного круга (рис. 31, б). Тогда CO = OD = 7,5 см.

2. Пусть PB = x. Тогда AP = 9 – x и по теореме об отрезках пере­секающихся хорд имеем AP ⋅ PB = CP ⋅ PD, или x (9 – x) = CP ⋅ PD.

3. Заметим, что CP = CO – PO = 7,5 – 6,5 = 1 (см). Кроме того, PD = PO + OD = 7,5 + 6,5 = 14 (см). Таким образом, x (9 – x) = 14. Отсюда находим, что x = 2 или x = 7. Следовательно, PB = 2 см и AP = 7 см или PB = 7 см и AP = 2 см.

О т в е т: 2 см, 7 см.