4.9. Рівняння лінійної регресії.

Розглянемо послідовність етапів визначення рівняння лінійної регресії для складної виробничої системи з одним виходом у і входами . Передбачається, що існує залежність

.

Задача полягає в перевірці правомірності припущення про наявність залежності такого виду та у знаходженні оцінок коефіцієнтів рівняння , що дають мінімум функції F:

Перш ніж приступити до складання системи нормальних рівнянь, необхідно виключити явні “викиди”, тобто такі експери­ментальні значення змінних, котрі не відповідають реальному процесу. Як правило, вони з'являються через нестабільність функціонування вимірювальної апаратури, ненадійності деяких елементів системи і т.п. Потім перевіряється значимість коефіцієнтів кореляції . Після цього рівняння регресії досліджується без тих , для яких незначно відрізняється від нуля. Крім того, оцінюється кореляція між параметрами і . Якщо і лінійно зв'язані між собою, то в шукане рівняння регресії потрібно включати тільки один з цих параметрів, тому що включення іншого параметра не вносить у це рівняння істотних змін (що справедливо лише в умовах проведеного дослідження).

Після вибору незалежних перемінних , що істотно впливають на вихідний параметр у, встановлюють правомірність припущення про лінійну залежність у від , для чого обчислюється коефіцієнт множинної кореляції

.

У залежності від кількості параметрів і довжини їхньої реалізації (кількості вимірювань) N за допомогою критерію Фішера і перетворення Ст’юдента встановлюється значимість коефіцієнта множинної кореляції R і коефіцієнтів регресії . Якщо R значимо відрізняється від нуля, то лінійна залежність між входами і виходами системи існує і припущення про наявність цього зв'язку вірне. У цьому випадку оцінюються коефіцієнти регресії .

У ході розрахунку потрібно також перевірити виконання третьої умови правомірності застосування регресивного аналізу: однорідність дисперсій. Для цього визначаються вибіркові дисперсії по кожній з N вибірок, знаходиться їхня сума, максимальне значення і складається відношення

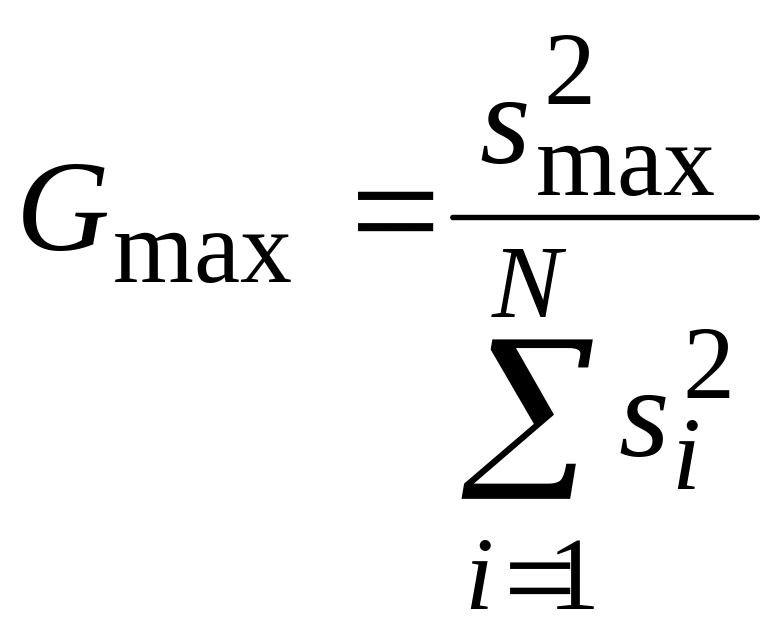, де .

Якщо дисперсії однорідні, то де — табульовані значення критерія Кохрена при рівні значимості р.

Приклад. Розглянемо опис механічних властивостей арматурної сталі 35ГС, отриманий знаходженням рівнянь множинної регресії — залежності механічних властивостей сталі від вмісту в ній окремих хімічних параметрів (зокрема, від швидкості d охолодження готового прокату, що виражається через площі поперечного перерізу профілів).

Математичні моделі цих залежностей для гарячекатаного металу мають вигляд

;

;

,

де , — відповідно границя текучості і міцності: —відносне подовження.

Для термообробленої сталі

;

;

.

Вище передбачалося, що відомо вигляд регресивної залежності. Більш часто зустрічається задача, коли необхідно знайти значення коефіцієнтів рівняння зв'язку, вигляд якого потрібно попередньо вибрати.

При наявності єдиної вхідний змінної розробка гіпотези про форму рівняння зв'язку спрощується, тому що дану залежність можна показати у виді графіка. Для цього весь діапазон зміни х на полі кореляції (мал. 4,7) розбивається на рівні інтервали . Усі точки, що потрапили в даний інтервал , відносять до його середини . Для цього підраховують часткові середні для кожного інтервалу:

.

Тут — число точок в інтервалі ; , де k — число інтервалів розбивки; N — обсяг вибірки.

Потім послідовно з'єднують точки відрізками прямої. Отримана ламана називається емпіричною лінією регресії у по х. По виду емпіричної лінії регресії можна підібрати рівняння регресії .

Якщо на значення у впливає безліч факторів , то представити таку залежність графічно неможливо. В цьому випадку розглядають ряд гіпотез про характер зв'язку між у і п факторами та за допомогою спеціальних критеріїв передбачувані залежності перевіряють на достовірність.

4.10. Нелінійна регресія.

Розглянемо нелінійну регресивну залежність. У загальному випадку будь-який регресивний зв'язок може бути записаний у вигляді

,

де — деякі обрані наперед функції.

Підстановкою вираз перетвориться до лінійної форми. Така заміна відповідає переходу від вихідних змінних до змінних х, простір яких називається лінеаризуючим.

Наприклад, якщо досліджується залежність швидкості хімічної реакції W від концентрацій компонентів і температури, зв'язок між ними часто має вигляд:

.

Логарифмуючи

і позначаючи

одержуємо

Основна трудність в задачах нелінійної регресії полягає у визначенні функцій тобто у виборі лінеаризуючого простору. У деяких випадках це можна зробити на основі аналізу механізму процесу, аналогічно випадку визначення швидкості хімічних реакцій. В інших випадках використовують тимчасові графіки. Так, якщо з графіка спостережень випливає, що крива регресії не може бути прямою, можна описати її за допомогою параболічної залежності деякого ступеня (квадратичної чи кубічної).

Коефіцієнти в таких рівняннях, наприклад, для полінома другого степеня при п змінних, визначають способами, аналогічними раніше розглянутим. Однак у цьому випадку не потрібно знаходити вибіркові коефіцієнти кореляції, що при нелінійній формі залежності між досліджуваними змінними втрачають зміст, а дослідження рівняння проводиться за статистичними критеріями (зокрема, адекватність моделі встановлюється за критерієм Фішера, як і у випадку лінійної регресії).

І в тому випадку, коли рівняння регресії являє собою поліном деякого степеня, за методом найменших квадратів коефіцієнти полінома знаходять розв’язуванням системи лінійних рівнянь. Наприклад, потрібно визначити за методом найменших квадратів коефіцієнти квадратичної функції у = f (х) - параболи другого порядку

.

Записуємо похідні функції по коефіцієнтам правої частини рівняння:

тоді система нормальних рівнянь має вид

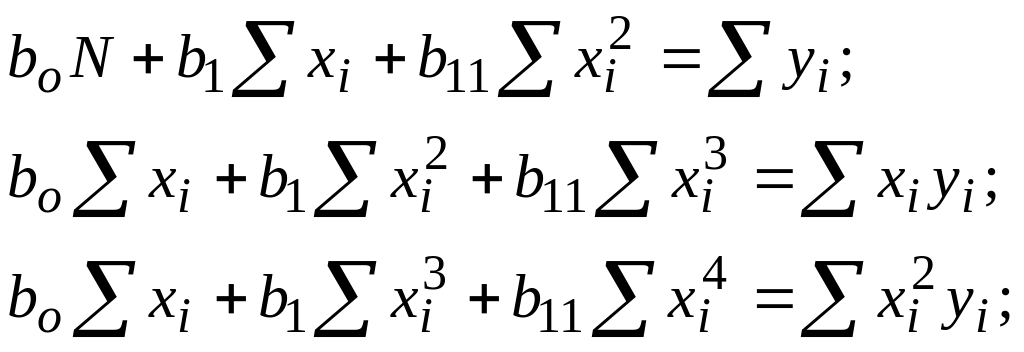
Можна перетворити поліноміальну модель другого порядку в лінійну, для чого позначимо . В результаті одержимо модель множинної лінійної регресії

.

До цього ж виду лінійної регресії можуть бути приведені багато інших видів моделей.

Експонентна модель для k змінних має вид

.

Прологарифмувавши обидві частини рівняння і позначивши одержимо лінійну регресивну модель

або .

Гіперболічна модель для k змінних має вигляд

Підставляючи в це рівняння , перетворимо його в лінійну регресивну модель

Однак отримані в такий спосіб коефіцієнти регресії можуть виявитися зміщеними оцінками для відповідних генеральних коефіцієнтів.

Приклад. Як приклад використання нелінійних регресивних рівнянь приведемо дані дослідження залежності продуктивності шліфування від основних факторів: глибини різання , зусилля притиску деталі до круга Р, зернистості круга , напруження на зазорі U .

Визначалися функціональні зв'язки наступного виду:

- для алмазного шліфування: ; при ;

для електроалмазного шліфування: ; ;при .

Тут індекс а відповідає функціональній залежності процесу шліфування при його інтенсифікації ультразвуковими коливаннями.

Залежності описуються поліномом другого степеня. Були отримані наступні рівняння:

;

;

Після розробки регресивної моделі проводиться аналіз достовірності моделі. При цьому потрібно установити, чи є гіпотеза, покладена в основу регресивної моделі, досить правильною, щоб з її допомогою робити прогнозування, і який ступінь точності може надаватися оцінкам, що одержуються за цією моделлю.

Експериментальні величини внаслідок помилок вимірювань і неадекватності моделі можуть відхилятися від прогнозованих значень . Ці відхилення (залишки) , якщо модель правильна, повинні підкорятися нормальному закону розподілу з нульовими середніми й однаковою дисперсією.

Якщо розподіл залишків відхиляється від нормального закону, варто з'ясувати, чи немає закономірної їхньої зміни в залежності від часу виконання чи від інших параметрів, що характеризують експеримент. Зокрема, потрібно з'ясувати, чи не зв'язане це відхилення зі зміною змінних, які вже ввійшли в рівняння. Може виявитися, що вони введені в рівняння в іншому від заданого вигляді. При виявленні серед залишків відхилень, більш ніж у три рази перевищуючих стандартне відхилення, необхідно проаналізувати причину таких відхилень і тільки при виявленні помилки в умовах проведення експерименту помилковий результат варто виключити з розгляду і повторити розрахунок рівняння регресії.

Остаточна перевірка адекватності моделі проводиться за допомогою статистичних критеріїв, зокрема, критерію Фішера. Вважається, що рівняння регресії адекватно описує досліджуваний процес, якщо залишкова дисперсія вихідної величини , розрахованої за рівнянням регресії відносно експериментальних даних , не перевершує в статистичному змісті дисперсію помилки досліду .

Залишкова дисперсія обчислюється по формулі

де — число ступенів свободи; N — кількість дослідів; m — число паралельних дослідів; — загальна кількість дослідів, результати яких використовують при підрахунку коефіцієнтів регресії; —число зв'язків (для лінійного полінома , — кількість факторів).

Щоб визначити дисперсію помилки досліду (дисперсію відтворюваності), необхідно мати кілька значень вихідного параметра, виміряних при однакових умовах (при тих же значеннях факторів). Для цього проводяться паралельні (дублюючі) досліди і значення в паралельних дослідах записуються в окремі графи таблиці вихідних статистичних даних. Потім обчислюються вибіркові дисперсії для кожної групи паралельних дослідів:

,

де - число паралельних дослідів ( );

- експериментальні значення вихідного параметра;

- середнє значення вихідного параметра за результатами паралельних дослідів.

Якщо вибіркові дисперсії по кожній групі паралельних дослідів однорідні, то помилка досліду

.

Число ступенів свободи, що характеризує цю дисперсію, . Лінійне рівняння регресії адекватно описує досліджуваний об'єкт, якщо виконується нерівність

де — значення критерію Фішера ( - критерію), яке варто знаходити по таблицях розподілу Фішера для обраного рівня значимості q (у технічних дослідженнях звичайно (q=5%).

65