
Міністерство
освіти і науки, молоді та спорту України
ДВНЗ
«Рівненський коледж економіки та
бізнесу»
В.
В. Білецький
МЕТОДИЧНІ
ВКАЗІВКИ до
вивчення предмету «Вища
математика»
Рівне
– 2012
Укладач:
В. В. Білецький
- викладач математики та фізики РКЕБ.
Рецензенти:
У даному посібнику
стисло викладено теоретичний матеріал
з окремих питань вищої математики, що
винесені на самостійне опрацювання
студентам згідно з навчальною програмою
для вищих навчальних закладів І - ІІ
рівнів акредитації.
Підручник містить
відомості про елементи лінійної алгебри,
аналітичну геометрію, границі функцій,
диференціальне та інтегральне числення,
диференціальні рівняння та числові
ряди.
Математичні
формули супроводжуються поясненням.
Кожний розділ завершується практичними
вправами та запитаннями на які необхідно
дати відповідь при опрацюванні даного
матеріалу.
Даний посібник
допоможе студентам за короткий термін
повторити основні поняття, теореми та
формули з вищої математики, а також
підготуватись до складання іспиту.
Розглянуто та
затверджено на засіданні ц /к природознавчих
та фізико-математичних дисциплін
Протокол №5 від
5 січня 2012 року
Голова ц /к Білецький
В. В.
Міністерство
освіти і науки, молоді та спорту України
ДВНЗ
«Рівненський коледж економіки та
бізнесу»
МЕТОДИЧНІ
ВКАЗІВКИ до
вивчення предмету «Вища
математика»
Рівне - 2012
ПЕРЕДМОВА
Успішна реалізація
досягнень науково-технічного прогресу
тісно пов’язана з використанням
математичних методів і засобів
обчислювальної техніки при розв’язанні
задач із різних областей людської
діяльності. Виключно важливе значення
має використання математичних методів
при побудові та розв’язанні економічних
задач та проблем, особливо у наш час,
коли економіка повинна відігравати
провідну роль у становленні та відродженні
нашої країни.
У даному підручнику
коротко висвітлено питання, які
виносяться на самостійне опрацювання,
але які є одночасно невід’ємною
складовою всього курсу вищої математики.
Практичні завдання, які включені до
складу посібника, передбачають набуття
студентами практичних навичок, необхідних
для: Закріплення
теоретичних знань; Розв’язання
теоретичних і практичних задач з
економіки із застосуванням математичного
апарату досліджень; Побудови
економіко-математичних моделей. Після
вирішення завдань, зазначених у посібнику
у повному обсязі студенти зможуть: Розв’язувати
системи лінійних алгебраїчних рівнянь
методами Крамера, Гаусса, матричним
методом. Обчислювати
визначники п-го порядку; Виконувати
дії над векторами; Складати
рівняння ліній та будувати криві
другого порядку; Знаходити
екстремуми функцій багатьох змінних; Проводити
дослідження та будувати графіки
функцій; Знаходити
невизначений та визначений інтеграли; Обчислювати
площі криволінійних трапецій; Досліджувати
на збіжність та знаходити суму числових
рядів; Розкладати
елементарні функції у ряд Маклорена.
Мета:
Засвоїти поняття матриці , оберненої
матриці та визначника матриці. Набути
навичок виконувати елементарні
перетворення матриці для знаходження
рангу матриці та оберненої матриці, а
також обчислення визначників другого,
третього та вищих порядків. Дати практику
розв’язування систем лінійних
алгебраїчних рівнянь методом Крамера
та матричним методом.
1.
Ранг матриці. Знаходження рангу матриць
з використанням елементарних перетворень.
2.
Обернені матриці. Знаходження оберненої
матриці.
3. Розв’язування
систем лінійних алгебраїчних рівнянь
метод Крамера та матричним методом.
Література:
[1] Ч.
1, $3, [2] P.3,
[4] P.1,
[6] P.14,
[7] P.2
1.
Рангом матриці називається
найбільший порядок відмінного від нуля
мінора матриці. Позначається через RgA
= r. Ранг нульової матриці дорівнює нулю. Елементарні
перетворення матриці: Властивість
1. При транспонуванні матриці її ранг
не змінюється. Властивість
2. Ранг матриці не змінюється, якщо
переставити її рядки ( стовпці). Властивість
3. Ранг матриці не зміниться, якщо
помножити всі елементи її рядка (
стовпця) на відмінне від нуля число. Властивість4.
Ранг матриці не зміниться, якщо до
одного з її рядків (стовпців) додати
інший рядок (стовпець), помножений на
деяке число. Властивість5.
Ранг матриці не зміниться, якщо вилучити
з неї рядок (стовпець), що дорівнює
нулю.
Дві матриці
називаються еквівалентними, якщо
від однієї з них до іншої можна перейти
за допомогою скінченої кількості
елементарних перетворень.
Наприклад,
матриця А
має єдиний мінор
четвертого порядку. який дорівнює нулю.
Серед мінорів третього порядку є мінор
який відмінний
від нуля. Отже, Rg A = 3
2. Квадратна
матриця А називається не виродженою
або неособливою, якщо її визначник
відмінний від нуля, тобто det A = 0 .
Квадратна матриця
А-1 зветься оберненою до квадратної
матриці А, якщо виконується рівність
А А-1= А-1А = Е, де Е - одинична
матриця того ж порядку, що і А та А-1.
Обернена матриця
А-1 знаходиться за формулою:
А-1 = 1/detA
де А - алгебраїчне
доповнення до елементів матриці.
3. Система
трьох лінійних рівнянь з трьома змінними
має вид:
а1 х +b1
y + c1 z = d1
а2 х +b2
y + c2 z = d2
а3 х +b3
y + c3 z = d3
Розв’язком
системи є невідомі величини, які будуть
задовольняти умову кожного із рівнянь.
Для розв’язку використовують метод
Крамера, метод Гаусса та матричний
метод.
a1 b1
c1
Якщо визначник
системи = a2
b2 c2 = 0 ,
a3 b3
c3
то система має
єдиний розв’язок, який
знаходять за формулами Крамера :
х = х
/ ,
y = y
/ , z = z
/ .
Якщо
= 0, то система або невизначена, або
несумісна. Невизначена має безліч
розв’язків (
х = 0, у
= 0, z = 0 , а
несумісна - жодного.
Матричним рівнянням
будемо називати рівняння вигляду АХ = В чи ХА = В
, де А та В - задані
квадратні матриці n-го порядку, а Х -
невідома матриця того ж порядку.
Розв’язком
матричного рівняння називається кожна
матриця відповідного порядку, яка,
будучи підставлена в матричне рівняння
замість матриці Х, перетворює рівняння
в тотожність.
Якщо detA = 0, то
матричні рівняння мають єдиний розв’язок.
А-1АХ = А-1
В, або Х = А-1 В
ХАА-1 = ВА-1,
або Х = В А-1
Очевидно, що
матриці А-1В та ВА-1 є
розв’язками рівняння.
А11 А21
... Аn1
А-1 = 1/detA
А12 А22 ... Аn2
А13 А23
... Аn3
де Аij -
алгебраїчні доповнення елементів до
матриці А.
Перевір себе.
Що називаємо
рангом матриці?
Які властивості
характерні для знаходження рангу
матриці?
Яку матрицю
називають оберненою?
Що називаємо
системою рівнянь.
У чому полягає
особливість розв’язку системи рівнянь
методом Крамера?
Як розв’язується
система матричним методом?
Розв’яжи.
1. За допомогою
елементарних перетворень матриці
знайти ранги матриць та виконати
операції над матрицями: А + 2В-1,
3В * СТ .
1 2 3 3
- 1 0 1 - 1 3 5
А = 3 6 9 В =
2 0 1 С = 2 1 -1 4
1 1 1
1 -1 2 2 -2 6 3
2. Розв’яжіть
системи рівнянь методом Крамера,
методом Гаусса та матричним методом.
2х
- у + z = 2 x + 2y +3z = 5 x + 2y - z = 2 3x
+ 2y + 2z = -2 2x - y - z = 1 2x - 3y + 2z =2 x
- 2y + z = 1 x + 3y + 4z = 6 3x + y + z = 8
3.
Знайти обернені матриці до матриць А
, В та С
-1 0 2
-1 - 1 2 -1 1 3
А = 1 2 1 В =
2 0 1 С = 2 2 -1
0 1 1
1 1 1 1 3 2
Мета:
З’ясувати поняття: вектор, векторний
простір, лінійна залежність та лінійна
незалежність векторів, базис векторного
простору. Ознайомитись
з різновидами рівняння прямих на площині
та в просторі. Навчитись виконувати
дії з векторами, обчислювати довжину
вектора, кут між векторами та скалярний
добуток векторів. Навчитись знаходити
кут між прямими, відстань від точки до
прямої, записувати рівняння прямих та
кривих другого порядку.
Вектори.
Векторні простори. Розклад вектора за
базисом. Кут
між площинами. Відстань від точки до
площини. Взаємне
розташування прямої і площини у
просторі. Криві
другого порядку на площині: коло, еліпс,
гіпербола, парабола.
Література:
[1] Ч.
1,Г.1 $2,Г.2 $$4-5, [3] P.1-3,
[4] P.5,
[6] P.17-22, [7]
P.14-18/
1. В природі
зустрічаються два види величин: скалярні
та векторні. Скалярні величини задаються
числами (температура, ціна, розмір ).
Векторні величина задаються векторами
(сила, швидкість, прискорення).
Вектором
(геометричними векторами) а називають
множину всіх напрямлених відрізків,
що мають .довжину і напрям.
Координати
вектора шукаються за наступними
формулами
А( х1 ; у1
), В(х2 ; у2 ) АВ
= ( х2 - х1 ; у2 - у1
) . Модуль вектора або довжина вектора
| AB| =
За цією формулою
обчислюють також відстань між двома
точками на площині.
Вектор нульової
довжини називають нуль - вектором.
Вектори, які лежать на
одній прямій або паралельних прямих
називають колінеарними. Вектори,
що лежать в одній або паралельних
площинах називають компланарними.
Якщо вектори співнапрямлені і мають
однакові модулі , то такі вектори ,
називають рівними.
Впорядкована
трійка одиничних векторів е 1, е
2 ,е 3 називається базисом
в множині всіх геометричних векторів
R3. Довільний геометричний вектор а може
бути єдиним чином представлений у
вигляді
а=х1 е1
+ х2 е2 + х3 е3 ,
число х1 ,х2
,х3 - називають координатними
векторами в базисі <е1,е2,е3>
Якщо задані два
лінійно незалежні вектори е1 та
е2, що лежать в одній площині то
кожний вектор а , що лежить в цій площині
можна представити у виді:
а=х1 е1+х2
е2
2. Нехай Р
- деяка площина, М0 (х0 , у0
, z0 )- точка яка належить цій
площині, а n=(А; В; С) - ненульовий вектор,
який є перпендикулярним до площини і
носить назву нормальний. Рівняння
площини матиме вид:
А ( х - х0
) + В (у - у0 ) + С (z - z0
) = 0
Кут між двома
площинами дорівнює куту між їх нормальними
векторами.
Нехай дві площини,
які перетинаються
А1 х + В1
у + С1 z = 0 i А2 х + В2 у +
С2 z = 0,
мають нормальні
вектори n1 = (A1 ; B1 ; C1)
i n2= (A2; B 2; C 2).
Тоді кут між цими площинами обчислюють
за формулою:
Умова паралельності
площин А1 /А2 = В1 /В2
= С1 /С2
Умова перпендикулярності
площин А1 А2 + В1 В2
+ С1 С2 = 0
Якщо площина
задана загальним рівнянням
А х + В у + С z = 0, то
нормуючи його і підставляючи потім на
місце довільних координат координати
точки М0 , отримаємо формулу для
обчислення відстані в координатній
формі:
d =
3. Пряма і
площина у просторі можуть перетинатись
під довільним кутом, бути перпендикулярними,
паралельними, мимобіжними.
Кут f між прямою
і площиною в просторі вимірюється
гострим кутом між прямою та її проекцією
на площину.
Нехай пряма і
площина задані рівняннями :
Отжe,
Умова паралельності
прямої і площини
Al+ Bm +
Cn = 0
Умова перпендикулярності
прямої і площини
4. До кривих
другого порядку відносяться: коло,
еліпс, гіпербола та парабола.
Колом називається
множина всіх точок площини, рівновіддалених
від даної точки цією площини, яка
називається центром.
Рівняння кола з
центром у точці О (а; b) і радіусом r має
вигляд
( х - а)2
+ (у - b)2 = r2
Еліпсом називають
геометричне місце точок площини , сума
відстаней кожної з яких до заданих
точок цієї ж площини , що називають
фокусами, є величина стала.
Рівняння еліпса,
фокуси якого лежать на осі ОХ, має вигляд
де а - довжина
великої півосі; b - довжина малої півосі.
Залежність між параметрами a, b, c
виражається співвідношенням а2
- b2 = c2.
Гіперболою
називають геометричне місце точок
площини, модуль різниці відстаней
кожної з яких до двох даних точок, які
називають фокусами, величина стала.
Рівняння гіперболи,
фокуси якого лежать на осі ОХ, має вигляд
де а - довжина
дійсної півосі; b - довжина уявної півосі.
Залежність між
параметрами а,b i c визначається
співвідношенням
b2 = c2 - а2
.
Ексцентриситетом
гіперболи називається відношення
фокусної відстані до її дійсної
півосі: е = с / а
Гіпербола
має дві асимптоти, рівняння яких має
вид
у = +
Параболою
називають множину точок на площині,
рівновіддалених від даної точки, яку
називають фокусом, і від даної прямої,
яку називають директрисою.
Рівняння параболи
з вершиною в початку координат, віссю
симетрії якої є вісь ОХ і вітки напрямлені
вправо, має вигляд
y2 =2px
де р> 0 ( параметр
параболи) - відстань від фокуса до
директриси. Рівняння її директриси х
= - р/2
Перевір себе.
Що називаємо
вектором, властивості векторів.
Як розкласти
вектор за базисними векторами.
Рівняння площини,
знаходження кута між площинами.
За якою формулою
знаходимо відстань між точками на
площині?
Умови розміщення
прямої і площини у просторі.
Що називаємо
кривими другого порядку. Які види
кривих є їх загальні рівняння.
Розв’яжи.
Дані точки А(3,
-1) і В(3, -4). Знайти координати векторів
АВ і ВА та ії модулі.
Дані вектори
а=(2,3) , с( -1, 2) , в(3, 1). Знайти координати
векторів: а + в, -3а + с, (а +2с) - (4а + с).
Визначити вид
трикутника АВС, якщо : А(1,3), В(2,-1), С(4,6).
Задані чотири
вектори a, b, c, d. Перевірити, чи утворюють
ці вектори базис у просторі R3,
та знайти координати вектора d у цьому
базисі, якщо
a = (2, 1, 0) , b= (4, 3,
-3), c = ( -6, 5, 7 ) , d = ( 34, 5, -26 )
Скласти рівняння
площини, яка проходить через вісь ОZ і
через точку M (1; 1;1).
Знайдіть гострий
кут між площинами х - у + z + 1 = 0 i 2x + 3y - z
- 3 = 0.
Перевірте, що
пряма (х - 1)/2 = (у + 3)/ (-1) = ( z - 4) / 5 лежить
у площині
3 х - 4у - 2z - 7 = 0.
Скласти канонічне
рівняння еліпса з фокусами на осі Ох,
якщо дані осі 2а = 12, 2b = 8.
Скласти канонічне
рівняння гіперболи, якщо відомі
координати її вершин А1(-3; 0), А2(3,
0) та координати фокусів F1(-5, 0),
F2(5, 0).
Мета:
З’ясувати поняття функціональної
залежності між величинами; дослідити
властивості основних елементарних
функцій;
навчитись
знаходити область визначення функції.
Засвоїти поняття: числова послідовність,
види послідовностей; навчитися знаходити
границі збіжних послідовностей та
точки розриву функцій.
Дослідження
властивостей основних елементарних
функцій. Поняття
числової послідовності, приклади
числових послідовностей, границя
послідовності. Точки
розриву функції та їх класифікація.
Література:
[1] Ч.
1, $4-5, [2] P.4-5,
[4] P.6,
[6] P.3-5.
1. Якщо кожному
елементу х з деякої множини Х за певним
правилом поставлений у відповідність
єдиний елемент y з множини Y, то кажуть,
що у є функцією від х і пишуть у = f(x).
Змінну величину х називають незалежною
змінною, або аргументом, а у - залежною
змінною, або функцією.
Розрізняють
функції: зростаючі та спадаючі, парні
та непарні, періодичні та неперіодичні.
Функція може бути
задана: математичною формулою, таблицею,
графіком, словесно, алгоритмічно.
До основних
елементарних функцій відносять наступні
функції: степенева, показникова,
логарифмічна та тригонометричні
функції.
Степенева
функція - y = xn, y = x1/n Показникова
функція - y = ax, a>0, a = 1. Логарифмічна
функція - y = loga x, a > 0, a
= 1. Тригонометричні
функції - y = sin x, y = cos x, y = tg x, y = ctg x
2.Нескінченною
числовою послідовністю називається
числова функція, визначена на множині
N натуральних чисел. Послідовність
називається зростаючою (спадною), якщо
кожний її член, починаючи з другого,
більший (менший) від попереднього. Послідовність
називається обмеженою зверху (знизу),
якщо можна назвати таке число М ( число
m), що для всіх членів цієї послідовності
виконується нерівність xn < M (
xn > m ). Числа M i n відповідно
називаються верхньою і нижньою межами
послідовності.
Число
а називається границею послідовності
( xn), якщо для будь-якого додатного
числа
Послідовність
може мати лише одну границю. Якщо
послідовність має границю, то таку
послідовність називають збіжною;
послідовність, яка не має границі,
називають розбіжною. Якщо
послідовність ( хn) має границею
число а, то пишуть lim xn = a. У цьому
разі кажуть, що послідовність збігається
до числ а
Теорема
Вейєрштрасса. Якщо послідовність
монотонна і обмежена, то вона має
границю. Обмеженість
послідовності є необхідною умовою
збіжності. Теореми
про границі.
Якщо послідовності
(xn) i ( yn) збігаються, то
lim (xn +
yn)=
Якщо послідовності
(xn) i ( yn) збігаються
lim (xn * yn)=
(
Сталий множник
можна винести за знак границі
Якщо
послідовності (xn) i ( yn)
збігаються і границя послідовності
(уn) відмінна від нуля, то
Послідовність
називається нескінченно малою, якщо
її границя дорівнює нулю і нескінченно
великою, якщо її границя дорівнює
нескінченність. Якщо (аn) -
нескінченно велика послідовність то
1/ (аn) - нескінченно мала і навпаки.
3.
Якщо функція y = f (x) при х = а має
розрив, то, щоб зясувати
характер розриву, треба знайти границю
функції y = f (x) при х -- а зліва і справа. Залежно
від характеру поводження функції в
околі точки розриву розрізняють два
основні види розривів: 1)
розрив 1 роду - у цьому випадку існують
скінченні границі lim f (x); 2)
розрив 2 роду - у цьому випадку хоча б
одна з границь не існує або нескінченна.
Перевір себе.
Означення функції
та їх класифікація.
Що називаємо
нескінченною послідовністю, та які
існують види.
Границя числової
послідовності.
Основні теореми
про границі
Нескінченно малі
та нескінченно великі послідовності.
Точки розриву
функції та їх класифікація.
Розв’яжи.
1. Дослідити
властивості та побудувати графіки
основних елементарних функцій.
2. Знайти область
визначення функцій:
1)
3) y = log2log3log4
x
3. Обчислити границі
1)
4. Знайти границі
функцій:
1)
3)
5)
Мета:
Закріпити поняття похідної функції та
її геометричного, механічного та
економічного змісту. Навчитись знаходити
похідні складних функцій та функцій,
заданих неявно і параметрично.
Відпрацювати вміння знаходити
диференціал. Дати практику
дослідження
функцій та побудови їх графіків.
Похідні
вищих порядків та їх застосування. Похідні
функцій, заданих неявно та параметрично. Використання
поняття похідної в економіці. Диференціал,
його геометричний та економічний
зміст. Найбільше
та найменше значення функції на
відрізку. Випуклість і вгнутість
кривої. Точки перегину.
Література:
[1] Ч.
1,Г.4, [2] P.6-7,
[4] P.7,
[6] P.7,9.
1. До поняття
похідної приводить ряд задач економічного,
геометричного та фізичного плану:
задача про продуктивність праці, задача
про миттєву швидкість та задача про
кутовий коефіцієнт.
Означення.
Похідною функції y= f(x) в даній точці
називається границя відношення приросту
функції до приросту аргументу, коли
останній прямує до нуля довільними
чином, тобто
Найбільш часто
для похідних приймають позначення
Читається
відповідно: “ігрек штрих”; “еф штрих
від ікс”; “де ігрек по де ікс”; “де еф
від ікс по де ікс”.
Означення.
Нехай функція у = f(x) має похідну f(x).
Похідна функції f(x)
називається другою похідною функції
у = f(x) і позначається через f(x).
Похідна від
похідної другого порядку називається
похідною третього порядку, аналогічно
n- порядку і позначається f(x),
fv(x), fn(x).
2. Теорема.
Будь-яка диференційована в точці функція
є неперервною в цій точці.
Якщо функція
диференційована, то вона має границю
в даній точці.
Оскільки існує
границя в даній точці, то вона неперервна
в даній точці.
Правила
диференціювання
1. Похідна сталої
дорівнює нулю С
= 0
2.Похідна суми
двох диференційованих функцій дорівнює
сумі похідних цих функцій, тобто (U(x)
+ V(x) = U(x)
+ V(x) Похідна
добутку двох диференційованих функцій
має вид
(UV)
= UV+V
U 4.
Похідна частки двох диференційованих
функцій має вид
Похідна складної
функції y=f(u), де u=(x) y(x)=f(u)*
(x)
Таблиця похідних
елементарних функцій
1. (xn)
= nxn-1; 6. (sin x)
= cos x; 10.
2. (ax)
= ax lna; 7. (cos x)
= - sin x 11.
3. (ex)
= ex; 8. (tg x)
= 1/cos2x = sec2x;12.
(logax)
= 1/x lna;9. (ctg x)
= - 1/sin2x = - cosec2x;
5. (lnx)
= 1/x; 13.
Похідна функції
х = х(у), оберненої до у = у(х) знаходиться
за формулою
ху
= 1/ух
Якщо функція y =
f(x) задана рівнянням F(x, y)=0, нерозв’язаним
відносно у, то вона називається заданою
неявно і її похідна ух
знаходиться за формулою
ух=
- Fx
/ Fy
Якщо функція y
=f(x) задана параметрично рівняннями х
= х(t),
y = y(t),
тоді похідна
визначається формулою ух
= yt /
xt
.
3. За допомогою
диференціального числення розглядають
загальні методи дослідження функції,
тобто встановлюють характерні особливості
зміни функції.
Однією із основних
задач, що мають застосування в економіці,
є знаходження оптимального розв’язку,
що дає максимальний прибуток при
мінімальних витратах. Як приклад можна
навести також задачі по знаходженню
еластичності попиту відносно ціни і
прибутку, еластичність пропозиції та
повних середніх витрат.
Приклад: Функція
попиту має вигляд q = 10 - p . Розрахувати
еластичність.
Еластичність
попиту рівна
Якщо, наприклад,
ціна за одиницю продукції рівна 6, то
Це означає, що
попит є еластичним. При ціні 6 грн. її
збільшення на 1 % приведе до зниження
попиту на 1, 5 %.
4. Нехай функція
y =f(x) диференційована при деякому
значенні змінної x, тоді:
f(x)
= dy/dx
Означення.
Диференціалом функції називається
головна частина її приросту, лінійна
щодо приросту аргументу:
dy = f(x)
d(x) (читається:”де ігрек”)
Властивості
диференціалу:
1. dc = 0;
2. d(uv)= du+ dv;
3. d(uv)= vdu + udv;
4.
Застосування
диференціалу базується на наближеній
рівності dy = y dx
1. Обчислення
наближеного значення приросту функції
dy = y dx
2.Обчислення
наближеного числового значення функції
3. Наближене
обчислення степенів
4. Наближене
обчислення коренів
5. Наближене
обчислення обернених величин
6. Наближене
обчислення синусів і тангенсів малих
кутів
7. Обчислення
табличних різниць десяткових логарифмів
5. Зростання
і спадання функції у = f(x) характеризується
знаком її похідної: якщо в деякому
проміжку f(x) > 0,
то функція зростає в цьому проміжку;
якщо ж f(x) < 0, то
функція спадає на цьому проміжку. Дані
проміжки називаються проміжками
монотонності.
Означення .
Точка х0 називається точкою
максимум(мінімум) функції f (x), якщо
існує окіл х0, що для х
, що належать цьому околу
f (x) - f (x0) <
0, (f (x) - f (x0))>0
Термін ”максимум”
та “мінімум” об’єднують загальним
терміном ”екстремум” ( від латинського
extrema-крайній).
Значення функції
в точці екстремуму називають екстремумом
функції. Точками екстремуму можуть
бути тільки точки 1 роду, тобто точки ,
що належать області визначення функції,
в яких похідна f (x) перетворюється в
нуль або зазнає розриву.
Означення.
Функція називається опуклою(угнутою)
на інтервалі, якщо її графіки лежать
нищу (вище) точок дотичних, проведених
до графіка функції в кожній точці
інтервалу (крім точок дотику).
Якщо в деякому
проміжку f (x)>0, то крива опукла вниз у
цьому проміжку; а якщо f(x)<
0, то крива опукла вгору в цьому проміжку.
Означення.
Точка, в якій функція змінює опуклість
на угнутість, називається точкою
перегину функції.
(Необхідна умова
перегину). Друга похідна f(x)
двічі диференційованої функції у точці
перегину х0 дорівнює нулю, тобто
f(x) = 0.
Перевір
себе.
1. Що таке похідна?
Геометричний, фізичний та економічний
зміст похідної.
2. Правила
диференціювання функцій заданих неявно
та параметрично.
3. Що називаємо
диференціалом функції? Практичне
застосування.
4. У чому полягає
правило знаходження найбільшого та
найменшого значення функції. За яких
умов функція опукла вверх ( вниз)?
Умови перегину
функції.
Розвяжи.
1. Знайти похідні
третього порядку для функцій:
а) у = х3
2х b) у = х
lnx c) y = x e-x
d) y = ex cosx
2. Знайти похідні
першого та друго порядків заданих
параметрично функціями х =(t),
y = (t), де t - параметр:
а) х = cos t b) x
= t2 c) x = et cost
y = sin t
y = t3 + t y = et sint
3. Знайти похідні
функцій, заданих неявно:
а) x siny - y cosx = 0 b)
exy - x2 + y2 = 0 c) xy + lny - 2
lnx = 0
4. Обчислити
наближено:
а) 100,99 b) 1,
02510 c) ln (1, 055) d) e0,07 e)
103lg2,994 .
5. Знайти інтервали
опуклості, угнутості, точки перегину
та найбільше і найменше значення функції
на вказаному інтервалі.
a) y = 3x5 - 5x4
+ 4 , [-3; 7] b) y = (x - 1)4 , [ -1; 6]
c) y = 2x2 + lnx, [ 2; 6]
Мета:
Засвоїти поняття функції багатьох
змінних. Дати практику обчислення
границь функцій багатьох змінних.
Навчитися обчислювати наближено
значення функції в точці, замінюючи її
повний приріст повним диференціалом.
Закріпити навички знаходження частинних
похідних першого та другого порядків
функцій двох змінних та навчитися
застосовувати їх до знаходження
екстремумів функцій двох змінних,
використовуючи необхідні умови існування
екстремуму функцій багатьох змінних
та достатні умови існування екстремуму
функцій двох змінних.
Способи
задання функцій багатьох змінних.
Лінії рівня. Границя та неперервність
функції двох змінних. Застосування
диференціального числення функцій
багатьох змінних до наближених
обчислень. Екстремум
функції. Найбільше і найменше значення
функції. Література:
[1] Ч.
1,Г.4, [5] P.7.
Функція, яка
залежить від кількох незалежних змінних
(х1, х2,
... хn ) називають функцією багатьох
змінних і має вигляд.
z = f (х1, х2,
... х n)
Незалежна змінна
х називається аргументом, а залежна
змінна z - функцією.
Сукупність значень
х1, х2, ... хn , для яких
вираз z = f (х1, х2, ... хn
) має зміст, називається областю
визначення функції, а значення, які при
цьому приймає залежна змінна, утворює
область значень функції.
Найбільше будемо
приділяти уваги функції від двох змінних
z= f(x; y)
Графіком функції
z= f(x;y) називається множина точок (х, у,
z), яка зображає деяку поверхню в R3.
Лінією рівня
функції z= f(x;y) називається лінія f(x;y)
= С на площині х0у, в точках якої
функція зберігає стале значення z= С.
Функція z= f(x;y)
називається неперервною у точці (х0,у0),
якщо існує границя.
2.
Якщо частинні похідні fx
і fy неперервні
в точці (х0; у0), то функція
f диференційована в точці (х0;
у0) ( достатня умова диференційованості
функції) При
досить малих х
та у для диференційованої
функції f в точці (х0; у0 ) має
місце наближена формула f
(x0, y0)
df (x0, y0), звідки
f (x0 + x
, y + y)
f ( x0, y0 ) + df(x0, yo)
f ( x0, y0
)+fx ( x0,
y0 )x+ fy
( x0, y0 )y
3. Означення.
Точка М0(х0,у0)
називається точкою максимуму(мінімуму)
функції z= f(x; y), якщо існує окіл точки
такий, що для всіх точок (х, у) цього
околу виконується нерівність
f(x0;y0)
> f(x; y) (f(x; y) > f(x0;y0))
Максимум і мінімум
функції називають її екстремумом Необхідна
умова існування екстремуму
Якщо функція
диференційована і має екстремум в
даній точці, то її частинні похідні
першого порядку дорівнюють нулю
fх
(x0; y0) = 0 і fу
(x0; y0) = 0 Достатня
умова існування екстремуму
Якщо функція z=
f(x; y) двічі диференційована в деякому
околі точки М0, то ввівши позначення:
А= fхх(x0;y0),
В= fху(x0;y0),
С = fуу(x0;y0),
=АС - В2 ,
будемо мати:
1) якщо
> 0 , то функція z= f(x;y) має в даній точці
екстремум, а саме: максимум А < 0( C<
0) і мінімум при А > 0 ( C > 0);
2) якщо
< 0 , то екстремум в точці М0 відсутній;
3) якщо
= 0, то потрібні додаткові дослідження.
Для відшукання
найбільшого і найменшого значення
функції в обмеженій області необхідно
знайти стаціонарні точки в середині
області і обчислити значення в цих
точках і на кінцях. Серед вибраних
значень знайти найбільше і найменше.
Перевір себе.
Що називаємо
функцією багатьох змінних?
Умова неперервності
функції багатьох змінних.
Формула застосування
функції багатьох змінних до наближених
обчислень.
Необхідна умова
існування екстремуму.
Достатня умова
існування екстремуму.
Розвяжи.
Обчислити границі
функцій багатьох змінних:
а)
Знайти частинні
похідні першого та другого порядків:
а) Z = 2x2y - 3y2
b) Z = x2siny c) Z = ln ( x2 -
y2)
Знайти повні
диференціали функцій двох змінних:
а) Z = xy2 b) Z
= ln (x + 5y2) c) Z = xy
cos xy
Обчислити наближено
значення:
а) (1, 08)3,96
b) 1, 942
e0,12 c) sin 1,59
tg 3,09
d) 2, 68sin0,05
5. Знайти екстремуми
функцій двох змінних:
a) Z = x3 +
8y3 - 6xy + 1 b) Z = x3 + 3xy2 -
15x - 12y с) Z = xy(1 - x - y)
Мета:
Засвоїти поняття первісної
функції, невизначеного інтегралу,
основні правила інтегрування, дати
практику знаходження невизначеного
інтегралу, що містить тригонометричну
та ірраціональну функції за допомогою
деяких спеціальних підстановок.
Навчитись на практиці застосовувати
вміння знаходити визначений інтеграл
до обчислення площі плоскої фігури,
довжини дуги плоскої кривої, об’єму
та площі поверхні тіла обертання. Дати
практику розв’язування диференціальних
рівнянь автономних та лінійних.
Інтегрування
тригонометричних функцій, інтегрування
ірраціональних функцій.
Основні властивості
визначеного інтегралу.
Обчислення довжини
дуги плоскої кривої, об’єму та площі
поверхні тіла обертання.
Автономні
диференціальні рівняння.
Лінійні
диференціальні рівняння зі сталими
коефіцієнтами. Література:
[1] Ч.
1,Г.6, [2]Ч.2,Г.2-3, [4] P.8,
[6] P.10-12. .
1. Основна
задача диференціального числення
полягає в тому, що за деякою функцією
треба знайти її похідну, якщо вона
існує. Основною задачею інтегрального
числення є обернена задача: за похідною
функції знайти саму функцію.
Означення.
Функція F(x) називається первісною для
функції y = f(x) на деякому інтервалі [a,
b], якщо F’(x) = f(x)x є
[a, b].
Якщо функція f(x)
має первісну F(x), то вона має нескінченну
множину первісних, які містяться у
виразі F + С, де С - стала.
Означення.
Множина всіх первісних для функції
f називається невизначеним інтегралом
і позначається
Властивості
невизначеного інтеграла
Таблиця
невизначених інтегралів
Безпосереднє
інтегрування ґрунтується на прямому
використанні таблиці інтегралів.
Від кожної
раціональної функції можна взяти
інтеграл, який виражається через
елементарні функції. Функція вигляду
I.
Інтеграли від
елементарних дробів обчислюються за
формулами
I.
II.
III. Якщо чисельник
дробу пропорційний похідній знаменника,
то інтеграл обчислюється за формулою
(4). В іншому разі чисельник розкладають
на суму двох доданків, один з яких
пропорційний похідній тричлена, а
другий сталий. Тоді інтеграл закусуємо
у вигляді суми двох інтегралів, перший
з яких обчислюємо за формулою (4), а
другий зводимо до інтеграла (6), виділенням
повного квадрата з тричлена.
IV. Інтеграл від
цього дробу зводиться до двох інтегралів,
перший з яких табличного типу
- кратного
інтегрування зводиться до табличного
Розглянемо деякі
класи функцій, які за допомогою певних
підстановок зводяться до раціональних
функцій, що завжди інтегруються.
І. Інтеграли
вигляду
ІІ. Інтеграли
вигляду
ІІІ. Інтеграли
вигляду
ІV. Інтеграли
вигляду
V. Інтеграли вигляду
sinmx cosnxdx, m, n e Z, обчислюються
так. Якщо n- непарне додатне число, то
застосовують підстановки sinx = t, а якщо
m - непарне додатне число, то підстановка
cosx = t. Якщо m i n- парні невід’ємні числа,
то пониження степеня здійснюється
внаслідок переходу до подвійного
аргументу за допомогою тригонометричних
формул пониження степеня:
VI. Інтеграли
вигляду
sinmx cosnx = 1/2(sin(m-n)x +
sin(m+n)x)
сosmx cosnx = 1/2(cos(m-n)x+
cos(m+n)x)
sinmx cosnx = 1/2(sin(m-n)x +
sin(m+n)x)
sinmx sinnx = 1/2(cos(m-n)x -
cos(m+n)x)
VII. Інтеграли
вигляду
2. Визначеним
інтегралом від функції f(x) на відрізку
[a, b ] називається границя інтегральної
суми за умови, що довжина найбільшого
з елементів відрізка прямує до нуля:
Числа а і b
називаються відповідно нижньою і
верхньою межами інтегрування.
Економічний
зміст визначеного інтегралу.
Нехай функція y=
f(t) характеризує зміну продуктивності
праці деякого підприємства за певний
час, то визначений інтеграл дає можливість
обчислити об’єм продукції , що випущена
за проміжок часу [0,T]
О с н о в н і в л а
с т и в о с т і в и з н а ч е н о г о і н т
е г р а л а
Визначений інтеграл
обчислюється за формулою Ньютона -
Лейбніца:
3. Поняття
визначеного інтеграла досить широко
використовують у фізиці, економіці та
в різного роду математичних дослідженнях.
Робота A, що
виконується змінною силою f(x) на шляху
від а до b обчислюється за формулою
Сила тиску рідини
на вертикальну пластинку обчислюється
за формулою:
Маса криволінійної
трапеції та статистичні моменти
обчислюється за формулами:
m = S = ydx Mx
= 1/2 y2 dx My= xydx
Обчислення шляху
пройденого тілом за певний час, якщо
відомо функцію швидкості:
S = v(t) dt
Обчислення площі
плоских фігур здійснюється за формулою:
S = f(x) dx
Обчислення об’ємів
тіл обертання навколо осі ОХ та ОУ
здійснюється за формулами:
Vx = n f2
(x)dx Vy = n g2 (y) dy
Нехай плоску криву
АВ задано рівнянням y= f(x) ( a< x <b),
причому f(x) i f(x) - неперервні функції в
проміжку [a; b]. Довжину дуги плоскої
фігури АВ обчислюють за формулою:
L =
4. Математичний
опис найрізноманітніших процесів, які
відбуваються у природі, часто приводять
до рівнянь, що зв’язують незалежні
змінні, шукану функцію і похідні або
диференціали цієї функції. такі рівняння
називаються диференціальними. Якщо
невідома функція є функція однієї
змінної, то диференціальне рівняння
називається звичайним. Якщо у
диференціальному рівнянні невідомою
є функція кількох змінних, тобто невідома
функція входить до рівняння разом зі
своїми частинними похідними, то рівняння
називається рівнянням з частинними
похідними. Порядком диференціального
рівняння називається порядок найвищої
похідної, яка входить до рівняння.
Диференціальне
рівняння першого порядку має вигляд
F (x, y, y’)
= 0 (1), або y’ = f(x, y),
(1а)
неявна і явна
форма запису, якщо воно розв’язане
відносно похідної.
Розв’язком
рівняння (1) або (1а) на інтервал (a, b)
називається диференційована на цьому
інтервалі функція y = q (x), яка
перетворює це рівняння в тотожність
при всіх х Є (а, b). Графік цієї функції
називається інтегральною кривою.
Загальним розв’язком
диференціального рівняння (1) або (1а) в
області D називається функція y = q (x, c),
яка і є розв’язком цього рівняння при
будь-яких допустимих значеннях С, і для
будь-якої початкової умови y(x0) =
y0 ((x0y0) Є D) і снує єдине
значення С = С0, при якому розв’язок
y = q (x, C) задовольняє дану умову.
Будь-який розв’язок
y = q (x, C0), який дістаємо з загального
розв’язку при конкретному значенні С
= С0, називається частинним.
5.Лінійним
диференціальним рівнянням першого
порядку називається таке диференціальне
рівняння, в яке у і у’ входять лінійно.
Його можна записати
так
A(x)y’+ B(x)y+
E(x)=0, (8)
або
y’ + P(x)y = Q(x) (9)
яке зводиться до
двох рівнянь з відокремленими змінними
за допомогою підстановки y = u(x)v(x)
Якщо в (1) Е(х)=0, а
в (2) Q(x)=0, то рівняння набирають виду
A(x)z’ + B(x)z=0 (10)
або
z’ + P(x)z=0 (11)
і називають
лінійними однорідними рівняннями. За
допомогою підстановки u(x)=x/y однорідне
рівняння зводиться до рівняння з
відокремленими змінними. Якщо в (8) Е(х)
0, а в (9) Q(x)=0, то
рівняння називають неоднорідними.
Перевір себе:
1. У чому полягає
дія інтегрування?
2. Основні властивості
невизначеного інтеграла.
3. Які підстановки
використовують при інтегруванні
тригонометричних та ірраціональних
функцій.
4. З якою метою
використовують визначений інтеграл?
5. Які рівняння
називають диференціальними? Як
розв’язуються автономні та лінійні
диференціальні рівняння.
Розв’яжи: 1.
Знайти невизначений інтеграл: а)
d) 2.
Обчислити довжину дуги плоскої кривої: а)
напівкубічної параболи у = х3/2
від х=0 до х=4 б)
кривої у = х2 від х = 0 до х = 2. 3.
Обчислити об’єм та площу поверхні
утвореної обертанням навколо осі ОХ: а)
півкола у =
b)
дуги синусоїди у = sin x від х = 0 до х = . 4.
Розв’язати автономін диференціальні
рівняння: а)
у + 4х = 0 b) y
= x + sinx c) y’ = e-3x 5.
Знайти загальні розвозки лінійних
диференціальних рівнянь: a)
y - y = ex b) y
+ x2y = x2 c) xy
+ y = lnx + 1
Тема
№ 7. Числові та степеневі ряди Мета:
Засвоїти поняття: знакосталі та
знакозмінні (знакопочергові) ряди,
абсолютна та умовна збіжність рядів.
Дати практику дослідження рядів та
застосування їх до наближених обчислень. 1.
Властивості збіжних рядів. 2.
Узагальнений гармонійний ряд. 3.
Застосування рядів до наближених
обчислень. Література:
[1] Ч.
2, , [2] Ч.2,Г9-10.
1. Розглянемо
будь-яку послідовність - числову або
функціональну - із загальним членом
un :
{un} = u1,
u2, ... , un ... .
Знак алгебраїчного
додавання між членами цієї послідовності
дає вираз, що містить нескінченне число
доданків і називається рядом:
u1
+ u2 +
u3
+ ... + un
+ ... =
Якщо доданки є
числами, то ряд називається числовим,
а якщо функціями, - то функціональним.
Загальний член ряду звичайно позначають
через un, an або fn(X).
Числа u1, u2, ... un, ...
навивають членами ряду.
Числові і
функціональні ряди можуть мати як
дійсні так і комплексні члени.
Числові ряди
можуть бути знаковизначеними і
знаконевизначеними, з додатними членами,
знакозмінними, знакопереміжними, з
комплексними членами.
У загальному
вигляді будемо користуватися такими
записами:
ряд з додатними
членами
a1+
a2
+ a3
... + an
=
знакопереміжний
ряд
a1
- a2
+ a3
- а4
... +(-1)n-1
an
=
(-1)n-1
an
знакозмінний ряд
a1
+ a2
+ a3
... + an
... =
an,
де an - дійсні числа будь-якого
знаку.
ряд з комплексними
числами
z1
+ z2
+ z3
... + zn
... =
,
де zn
= xn
+ iyn,
xn=
Rezn;
yn=
lmzn,
i=-1
функціональний
ряд
f1(x)+
f2(x)+
f3(x)
... + fn(x)+...
=
fn(x),
де fn(x)
- функція однієї або багатьох
змінних.
Функціональні
ряди поділяються також на дійсні і
комплексні. Залежно від типу функції
функціональні ряди можуть бути
степеневими, тригонометричними.
Означення.
Ряд називається збіжним, якщо існує
скінченна границя послідовності його
часткових сум, або
Число S називається
сумою ряду. Якщо скінченої границі не
існує, ряд називають розбіжним.
Властивості
збіжних рядів
1. Якщо ряд а1
+ а2 + ... + аn + ... збігається,
то і ряд а1 + а2 + ... + аn
+ ... збігається та має суму S, - деяке
число.
2. Якщо ряди аn
та bn збігаються і їх суми
відповідно рівні S1 та S2, то
і ряд (а1 + b1 ) +(а2 + b2
) + ... +(аn + bn ) + ... збігається
і його сума рівна S1 + S2.
3. Якщо ряд
збігається, то збігається ряд, отриманий
із даного відкиданням (приписуванням)
скінченого числа членів.
Необхідна ознака
збіжності
Якщо ряд збігається,
то границя його загального члену аn
при n дорівнює нулеві, тобто
an
= 0
2. Гармонійний
ряд - це ряд виду
1/n
= 1 + 1/2 + 1/3 +
... + 1/n + ... , даний ряд розбігається
( S =+)
Ряд утворений з
членів геометричної прогресії має
вид. Він збігається при | q | < 1 і його
сума S = a/1-q і розбігається при
| q | > 1
aqn-1
= a + aq + aq2
+ ... + aqn-1
+ ...
Якщо un >
0, то ряд називається додатним. Розглянемо
такі ознаки збіжності додатних рядів.
I. Нехай маємо два
ряди
un
(A) i
vn
(B)
а) Якщо un <
vn, n Є N, то із збіжності ряду (В)
випливає збіжність ряду (А), а з розбіжності
ряду (А) випливає розбіжність ряду (В)
( перша ознака порівняння).
б) Якщо
un/vn= r, 0 < r <+ ,
то ряди (А) і (В) одночасно збігаються
або розбігаються (друга ознака
порівняння).
II. Ознака Д’
Аламбера. Якщо для ряду
un
існує (скінчена або нескінченна)
границя
то при D < 1 ряд
збігається, а при D > 1 розбігається.
III. Ознака Коші.
Якщо для ряду
un
існує (скінчена або нескінченна)
границя
то при К < 1 ряд
збігається, а при К > 1 розбігається.
3. Користуючись
розкладом у степеневі ряди, можна
обчислювати наближені значення
визначених інтегралів, границі та ін.
У таких обчисленнях зберігають n перших
членів ряду, а останні відкидають. Для
оцінки похибки знайденого наближеного
значення потрібно оцінити суму відкинутих
членів, тобто залишок ряду Rn(x).
Рекомендується оцінку проводити так:
якщо ряд знакосталий, то його залишок
порівнюють з геометричним рядом, члени
якого утворюють спадну геометричну
прогресію, а якщо ряд знакозмінний і
його члени задовольняють умови теореми
Лейбніца, то використовують оцінку |
Rn(x)| < | un+1 |, де un+1 -
перший з відкинутих членів ряду.
Використовують
наступні розклади функцій:
ex
=
ln(1+x)
= x -
1. Що називаємо
рядом? Які існують види рядів?
2. Властивості
збіжних рядів.
3. Особливості
узагальненого гармонійного ряду.
4. Які розклади
використовують при знаходженні
наближених обчислень?
П.П.
Овчинников. Вища математика. –
К.:Техніка, 2000, Ч.1-2.-1180 с. За
ред. Г. М. Яковлєва. Алгебра і початки
аналізу.-К.:Вища школа, 1984,Ч 1-2.-586 с. За
ред. Г. М. Яковлєва. Геометрія.-К.:Вища
школа, 1978, Ч. 1-2.-300 с. С.
М. Пастушенко, Ю. П. Підченко. Вища
математика. – К.: Діал.,2002.-160 с. М.
К. Бугір. Математика для економістів.
– Т.: Підручники та посібники. 2001.-192 с. М.
В. Богомолов. Практичні заняття з
математики.К. Вища школа, 1979.-472 с. Ю.
К. Руданський. Лінійна алгебра та
аналітична геометрія.-Л.: “Бескід
Бід”,2002.-262с. М.
О. Давидов. Курс математичного аналізу.:К
Вища школа.1990.-384 с. М.
І. Шкіль. Математичний аналіз.-К.:Вища
школа.1994. –424 с. Л.І.
Дюженкова, Т.В. Носаль. Вища
математика.-К.:Вища школа, 1991.-408 с. В.
В. Барковський, Н. В. Барковська. Вища
математика для економістів.-К.:ЦУЛ,
2002.- 400 с. М.
Я. Выгодский. Справочник по высшей
математике.-М.:Наука,1966.- 870 с.
ЗМІСТ
Передмова 4 Тема
1: Елементи лінійної алгебри. 5 - 7 Тема
2: Аналітична геометрія. Векторна
алгебра 8 –11 Тема
3: Вступ до математичного аналізу. 12-14 Тема
4: Диференціальне числення функції
однієї
змінної. 15-19 Тема
5: Диференціальне числення функції
багатьох
змінних. 20-21 Тема
6: Інтегральне числення та
диференціальні
рівняння. 22-29 Тема
7: Числові та степеневі ряди. 30-32 Література. 33
Методичний посібник
видано видавництвом «Ідеал»
м Рівне, вул. Ст.
Бандери .
Тема № 1: елементи лінійної алгебри
![]()
![]()
![]()
Тема № 2: аналітична геометрія. Векторна алгебра.
![]()
![]()
![]()
![]() А
х + В у + С z +D = 0
А
х + В у + С z +D = 0![]()
![]()
![]() ( a >b ),
( a >b ),
![]()
![]()
Тема № 3: вступ до математичного аналізу.
![]() знайдеться натуральне число N, що при
всіх n > N виконується нерівність | xn
- a| <
.
знайдеться натуральне число N, що при
всіх n > N виконується нерівність | xn
- a| <
.
![]() .
.
![]() .
.
![]()
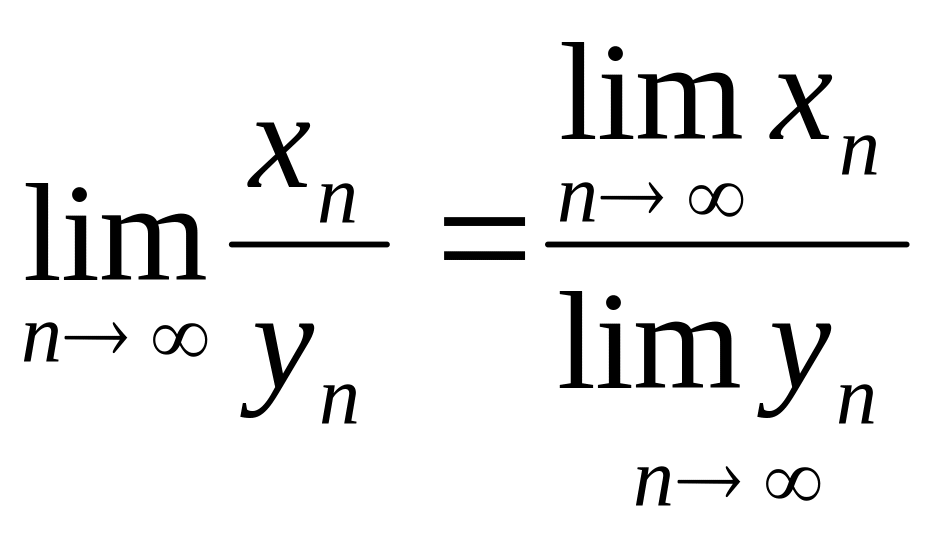
![]() 2)
y =
2)
y =
![]()
![]()
![]() ,
якщо загальні елементи послідовностей
задаються формулами:
,
якщо загальні елементи послідовностей
задаються формулами:![]() 2)
2)
![]() 3)
3)
![]()
![]() 2)
2)![]()
![]() 4)
4)
![]()
![]() 6)
6)
![]()
Тема № 4: диференціальне числення функції однієї змінної
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тема № 5: диференціальне числення функції багатьох змінних.
![]()
![]() b)
b)
![]() c)
c)
![]()
Тема № 6. Інтегральне числення
![]()
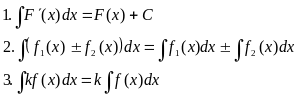
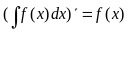
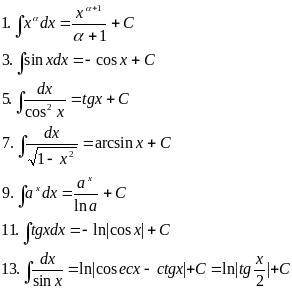


![]() ,
де Р(х) і Q(x) - многочлени, називається
дробово-раціональною, або раціональним
дробом. Дріб правильний, якщо степінь
многочлена Р(х) нижчий за степінь Q(х).
Якщо дріб неправельний з нього виділяють
цілу частину (многочлен), ділячи чисельник
на знаменник. Правильний дріб можна
подати у вигляді суми скінченого числа
елементарних дробів типу:
,
де Р(х) і Q(x) - многочлени, називається
дробово-раціональною, або раціональним
дробом. Дріб правильний, якщо степінь
многочлена Р(х) нижчий за степінь Q(х).
Якщо дріб неправельний з нього виділяють
цілу частину (многочлен), ділячи чисельник
на знаменник. Правильний дріб можна
подати у вигляді суми скінченого числа
елементарних дробів типу:![]() II.
II.
![]() III.
III.
![]() IV.
IV.
![]()
![]()
![]()
![]() , а другий
, а другий
![]() .
Останній інтеграл шляхом (n - 1)
.
Останній інтеграл шляхом (n - 1)
![]() за допомогою рекурентної формули
за допомогою рекурентної формули![]()
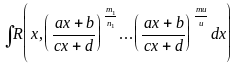 обчислюються за допомогою підстановки
обчислюються за допомогою підстановки
![]()
![]() зводяться до табличних інтегралів 13 і
15, виділенням повного квадрата у тричлені
зводяться до табличних інтегралів 13 і
15, виділенням повного квадрата у тричлені
![]()
![]() обчислюються так. У чисельнику дробу
утворюють похідну квадратного тричлена,
що міститься під знаком кореня. і
розбивають дріб на два дроби, перший з
яких інтегрують за формулою(5), а другий
зводять до випадку ІІ.
обчислюються так. У чисельнику дробу
утворюють похідну квадратного тричлена,
що міститься під знаком кореня. і
розбивають дріб на два дроби, перший з
яких інтегрують за формулою(5), а другий
зводять до випадку ІІ.![]() зводять до інтегралів від раціональних
функцій нової змінної t підстановкою
зводять до інтегралів від раціональних
функцій нової змінної t підстановкою
![]() (універсальна тригонометрична
підстановка). При цьому дістаємо
(універсальна тригонометрична
підстановка). При цьому дістаємо![]()
![]() обчислюються, використовуючи такі
формули:
обчислюються, використовуючи такі
формули:![]() за допомогою тригонометричних підстановок
x= acost (x= asint), x= atgt,
за допомогою тригонометричних підстановок
x= acost (x= asint), x= atgt,
![]() відповідно зводяться до інтеграла типу
IV , який раціоналізується.
відповідно зводяться до інтеграла типу
IV , який раціоналізується.![]()
![]()

![]()
![]()
![]()
![]() dx
, де а і b - значення незалежної змінної
х у точках А і В.
dx
, де а і b - значення незалежної змінної
х у точках А і В.![]()
![]() b)
b)
![]() c)
c)
![]()
![]() e)
e)
![]() f)
f)
![]()
![]() ;
;![]()
![]() an
an
> 0;
an
an
> 0;![]() Sn
= S
Sn
= S![]()
![]()
![]()
![]()
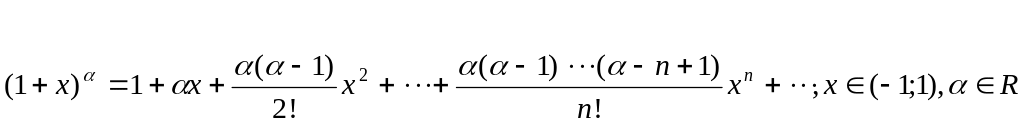 Перевір
себе:
Перевір
себе:Література
34
4
33
5
32
6
31
7
30
8
29
9
28
10
27
11
26
12
25
13
24
14
23
15
22
16
21
17
20
18
19
