3 В. В. Нащокин .65

определить и c_v, которую из опыта определить очень трудно. Следует отметить, что для реальных газов

Ср — c_v^> R.

Это неравенство объясняется тем, что при расширении реальных газов (при р = const) совершается ле только внешняя, но и внутрен­няя работа, связанная с изменением внутренней потенциальной энер­гии тела, что и вызывает больший расход теплоты.

§ 6-4. Элементы молекулярно-кинетической и квантовой теории теплоемкости

Классическая молекулярно-кинетическая теория газов рассматри­вает идеальный газ как совокупность абсолютно жестких молекул, между которыми отсутствуют силы взаимодействия и каждая молекула обладает лишь энергией поступательного и вращательного движения, а сами молекулы рассматриваются как материальные точки.

Поступательное движение такой молекулы можно разложить по направлениям трех, координатных осей, в соответствии' с этим говорят, что молекула имеет три степени свободы поступательного движения. Количество вращательных степеней евободы будет зависеть от атом­ности газа.

В соответствии с кинетической теорией внутренняя энергия газов равномерно распределяется по степеням свободы поступательного и вращательного движения молекул.

Одноатомный газ имеет только три степени свободы поступатель­ного движения (/ = 3). Молекула двухатомного газа кроме поступа­тельного движения может совершать и вращательное движение вокруг общего центра тяжести, который находится' на линии, сое­диняющей оба атома. Такая молекула двухатомного газа имеет пять степеней свободы (i = 5), из них три степени свободы поступательного движения и две степени свободы вращательного движения...

Молекулы трех- и многоатомных газов имеют три степени свободы поступательного движения и три степени свободы вращательного дви­жения, а всего I =6.

Для того Чтобы вычислить долю внутренней энергии, приходящую­ся на одну степень свободы, рассмотрим одноатомный идеальный газ, у которого имеется только три степени свободы поступательного дви­жения.

Из кинетической теории известно, что давление, оказываемое иде­альным газом на стенки, равно 2/3 средней кинетической энергии по­ступательного движения атомов, т. е.

р = (2/3) шЛ, - (6-17)

где р — давление газа, н/м²; п — число атомов в 1 м^г; т — масса од­ного атома; w — средняя квадратичная скорость атомов, определяемая

из уравнения

до² = (до? -f w\ 4- Доз 4- •" + Wn)/n,

где w_lt до₂, до_п — скорости отдельных атомов.

Умножая обе части уравнения (6-17) на объем киломоля Уц, полу­чим уравнение для 1 кмоль:

pV» = (2/3) пУ^пш²/2.

В этом уравнении произведение nVy. = N есть число атомов в 1 кмоль газа (число Авогадро):

pV» = (2/3) NmwV2.

Величина mwV2 представляет собой среднюю кинетическую энер­гию поступательного движения одного атома газа, а так как общее число атомов равно N, то вся внутренняя энергия 1 кмоль одноатом­ного газа, равная кинетической энергии всех атомов, равна

ци = Nm до²/2.

Тогда f.

pVy, - (2/3) ци, или ци = (3/2) pVa. (6-18) Заменяя pV_ß его значением из уравнения состояния, находим

. ци = (3/2) iiRT, (6-19) а так как \iR = 8,3142 кдж/(кмоль-град), то для одноатомного газа ци = (3/2).8,3142 Т = 12,5 Т. / (6-20

Взяв из уравнения (6-19) производную от внутренней энергии по температуре, -имеем

аци/dT = [ic_v = (3/2). pi?. (6-21)

Из уравнения видно, что цс_и не зависит от температуры. Следо­вательно, уравнение (6-19) выражает внутреннюю энергию одноатом­ного идеального газа, который подчиняется уравнению pVß = цЯТ и у.которого цс_и = const.

Численное значение мольной теплоемкости для одноатомного газа равно

цс„ = (3/2)р#, = 12,5 кдж/(кмоль * град).

Отсюда на каждую степень свободы движения в одноатомном газе расходуется энергия — 12,5 : 3 = 4,16 кдж/(кмоль-град). Подстав­ляя значение теплоемкости цс_ь из (6-21) в уравнение Майера, находим

цс_Р = [(/ 4- 2)/2]р#, ' ' (6-22)

или для одноатомного газа

цс_р = [(3 4- 2)/2]8,3142 я* 20,8 кдж/(кмоль-град).

Экспериментальные исследования для одноатомных газов подт­верждают полученные данные.

3* • 67

Для двухатомного газа, считая, что на каждую степень свободы движения расходуется количество энергии, как и для одной степени свободы поступательного движения одноатомного газа, находим:

рс₀ = 4,16-5 20,8 кдж/(кмоль-град), рс_р = [(5 + 2)/2]8,3142 » 29,1 кдж/(кмоль.-град).

Однако для сравнительно высоких температур получается значи­тельное несоответствие'приведенных значений теплоємкостей двухатом­ных газов с экспериментальными данными. Еще большее расхождение получается для трех- и многоатомных газов.

Это расхождение объясняется тем, что в сложных молекулах не­обходимо учитывать не только поступательное и вращательное движе­ние, но и колебательное движение атомов в самой молекуле, энергия которых в кинетическойтеории газов не учитывается.

Энергию колебательного движения атомов в молекуле учитывают в квантовой теории теплоємкостей. Эта теория доказывает, что тепло­емкость двух- и многоатомных газов является функцией температуры, так как энергия колебательного движения • атомов в молекуле из­меняется не прямо пропорционально температуре.

_ч Эйнштейн, пользуясь квантовой теорией Планка, получил следую­щее выражение для мольной теплоемкости, достаточно точное для тем­ператур, применяемых в теплотехнике:

^-i^RV+^R^JeWlieW-l)*, . (6-23)

где ~i_x -— число степеней свободы поступательного и вращательного движений молекулы; і₂ — число степеней свободы внутримолекуляр­ных колебаний; Ö — характеристическая температура колебательного движения, равная ö = ha/k (h — постоянная Планка, k — постоян­ная Больцмана, со — число колебаний в секунду): е—основание на­туральных логарифмов; Т — абсолютная температура газа.

Первый член правой части формулы (6-23) учитывает количество .энергии, идущей на изменение-поступательного и вращательного дви­жения молекул; он определяется числом степеней свободы этих" дви­жений. Второй член формулы учитывает энергию, идущую на изме­нение внутримолекулярных колебаний; он определяется числом колебательных степеней свободы.

Формула (6-23) не является абсолютно точной, так как .при ее вы­воде были сделаны некоторые допущения.

Для приближенных расчетов при не очень высоких температурах можно рекомендовать использование постоянных мольных теплоєм­костей цс₀ и рСр, полученных с некоторой корректировкой для трех-и многоатомных газов на основании молекулярно-кинетической тео­

рий теплоемкости. Эти данные Тіри-ведены в табл. 6-1.

Точные значения теплоємкостей идеальных газов в зависимости от температуры приводятся в специ­альных таблицах. Эти значения вычисляются на основании спек-' троскопических данных с исполь­зованием математического аппара­та квантовой статистики.

§ 6-5. Истинная и средняя теплоемкости

Так как теплоемкость идеального газа зависит от температуры, а реального и от давления, то в технической термодинамике различают истинную и среднюю теплоемкости.

Теплоемкость, определяемая уравнениями (6-1), (6-3), (6-4) при дан­ных значениях параметров состояния v и Т или р и Т (т. е. в данном состоянии тела), называют истинной теплоемкостью. Следовательно, истинной теплоемкостью называется отношение элементарного коли­чества теплоты, сообщаемой термодинамической системе в каком-либо процессе, к бесконечно малой разности температур.

Истинные теплоемкости реальных газов можно выразить в виде суммы двух слагаемых:

Сх e_XQ "f" Ас_х.

"Первое слагаемое представляет собой теплоемкость данного газа в разреженном (идеально газовом) состоянии (при р -*■ 0 или v со ) и зависит только от температуры.

Температурная зависимость теплоємкостей с_р и c_v приближенно может.быть представлена в виде полинома третьей степени от f С:

с_х0 = й₀ + aj + a₂t* + a₃t'^A. ■

Однако в настоящее время в расчетах используют более точные таблич­ные значения. '

Второе слагаемое Ас_х определяет зависимость теплоемкости от дав­ления или удельного объема и связано с изменением потенциальной составляющей внутренней энергии реального газа.

В практических расчетах при определении колйчества.теплоты обыч­но применяют та-к называемые средние теплоемкости.

Средней теплоемкостью с_хт данного процесса в интервале темпе­ратур от t_t до t₂ называют отношение количества теплоты q\.->. к ко­нечной разности, температур t₂ — 1_г:

с , " (6-24)

Так как количество теплоты 171.2, _х, полученное системой в про­цессе х = const, определяется уравнением (6-2), где с_х — истинная теплоемкость в данном процессе, то

^с«»й=-^Ьг1^с**- ⁽⁶"²⁵⁾

Уравнение (6-25) устанавливает связь межДу средней и истинной теплоємкостями тела в данном процессе.

Если средние теплоемкости даны в таблице для интервала темпе­ратур от 0- до Ґ С, то средняя теплоемкость с_хт$1 может быть вычис­лена по формуле

Г =

(6-26)

Действительно, интеграл в уравнении (6-25) на основании извест­ного из математики правила может быть разбит на следующие инте­гралы:

ti Р о

но

^схdt = c_xm |„²t₂, a c_xdt — c_xm |₀' ty о о

Подставляя найденные значения интегралов в уравнение (6-25), получаем уравнение (6-26).

Таким образом, если в каком-либо процессе идеальный газ был на­грет от температуры t_x до t₂, то количество теплоты, затраченное на нагревание, равно

Q* = m \c_xm 1о² к~с_хт \ї h) = V_a [с'_хт \t* t₂-c'_xm \i^l /J. (6-27)

Средние мольные, массовые и объемные теплоемкости газов при р = const и v = const приведены в табл. Ill, IV, V, VI, VII, VIII. приложения.

§ 6-6. Отношение теплоємкостей Ср и с_и ¹

В термодинамике часдо используется отношение теплоемкости при постоянном давлении'к теплоемкости при постоянном объеме, обозна­чаемое обычно буквой k: *

k = CpiCv = C'p/c'_v — рСр/рСц.

Согласно классической кинетической-теории газов величина к оп­ределяется числом степеней свободы молекулы. Из уравнений (6-21) и (6-22) следует

fe = i±2-./?: -L/г=1 ₊ 2/і. ' (6-28)

Если считать c_Ä=const, то из табл. 6.1 получаем: для одноатомного газа k = 1,66; для двухатомного газа £=1,4, для трех- и многоатом­ных газов k = 1,33.

При с_х ф const k для идеальных газов зависит от температуры, что и видно из формулы

И'= c_p/c_v = (c_v + R)lc_v — 1 4- R/c_D.

Из уравнения Майера можно получить следующие соотношения для теплоємкостей & и с_р:

c_v = Rl(k — 1); с_р = kRl(k - 1). (6-29)

§ 6-7. Определение <7„ и q_p для идеальных газов по таблицам теплоємкостей

Как уже указывалось, количество теплоты в изобарном н изохор-ном процессах идеального газа может быть подсчитано по следующим уравнениям:

Яр. і-» = Срт ti'h-c_vm I^і; и = h-h; (6-30)

Qv, ]-г = С_г,_т|о^2 — Cpmlo' /і = «2 — "і- (б'³¹)

Следовательно, для определения теплота <7_р'и ^."необходимо знать либо теплоемкости в интервале температур от 0 до f С, ли.бо значения энтальпий и внутренних энергий.

В настоящее время имеется большое количество пособий и специ­альных таблиц, в которых эти величины с высокой степенью точности даются для широкого интервала температур. Все новейшие данные по теплоємкостям, энтальпии и внутренней энергии рассчитаны с исполь­зованием уточненных спектроскопических констант методом кванто­вой статистики. Приведенная выше формула Эйнштейна для подсчета теплоемкости может, рассматриваться как первый шаг в создании со­временной квантовой теории теплоемкости.

В отечественной литературе подробные данные по теплоємкостям Ср и Со, а также энтальпии и внутренней энергии приведены в 18, 48, 58).

§ 6-8. Теплоемкость смесей идеальных газов

При расчетах тепловых установок приходится встречаться со сме­сями газов, а в таблицах приводятся теплоемкости только для отдель­ных идеальных газов; поэтому нужно уметь определить теплоемкость газовой смеси. Если смесь газов задана массовыми долями, то массовая теплоемкость смеси определяется как сумма произведений массовых

долей на массовую теплоемкость каждого газа:

с*, см = 81 с*1 + & ^2 + •' • + £_п с_т = 2 & с„, (6-32)

и

и

1

где £₁₍ ... —массовые доли каждого газа, входящего в смесь.

Если смесь газов задана объемными долями, то объемная теплоем­кость смеси равна сумме произведений объемных долей на объемную теплоемкость каждого газа:

п

< см - »1 с_а1 + г₂ с'_а2 -\ Ь г_п с1_п = 3 Г, Со, . , (6-34)

1

и -

п ,

с'р. см - ^ с'_р1 + г, си + • • • + г_п с;_п = 3 г, с^,, (6-35)

1

где г_ь г₂,..., г_п—объемные доли отдельных газов, входящих" в смесь.

Мольная теплоемкость смеси газов равна произведению объемных долей на мольные теплоемкости составляющих смесь газов:

п

№_У1 см =? /1 с_о1 + г₂ р₂ ^с^ + •' • + г„ р_п с„„ = 2 Г,- Р/ с_ы,

п

№_Р, см - Г\ Ні Срі + г₂ р₂ Срг + " • + г„ р„ с_р„ = ^ г, р; с_р„

і

где р — средняя молекулярная масса смеси газов; р₂, р_п — молекулярные массы отдельных газов.

Массовая теплоемкость смеси газов может быть определена, если известны плотность и удельный объем смеси газов при нормальных физических условиях:

см ⁼ £»,»ем ^см, о° ⁼ Сг>, см/Рем, о"

и

Ор, см ~А^р< см '■'см, о^{0 = с}», см/Рем, о^0-§ 6-9. Приближенные значения теплоємкостей*

Для приближенных расчетов иногда пользуются эмпирическими |юрмулами, учитывающими зависимость теплоемкости от температуры по линейному закону. Для истинной теплоемкости эта,зависимость может быть представлена уравнением вида

* § 6:9_приведен в'этом учебнике вынужденно, в связи с тем, что вся техни-іеская литература по расчету пищевых машин применяет'ураенение (6-37).

с* = а + Ы, . (6-36)

где а — истинная теплоемкость при 0° С; Ь — тангенс угла наклона прямой, ха_рактеризующий изменение теплоемкости от температуры.

1 '' $

Зная зависимость с_х = / (/), можно по (6-25) определить среднюю теплоемкость с_хт:

^2 -' ^2

/2-

1

/2-/1

«0*2

/2 /2

'2 «I

= * + -§-(/_а +/і)- (6-37)

§ 6-10. Энтропия. Вычисление энтропии идеального газа для обратимых и необратимых процессов

Как уже указывалось, теплота д не является функцией состояния и &д — йи + р&и не будет полным дифференциалом; (к/ представляет собой только некоторую бесконечно малую величину. Для того чтобы проинтегрировать правую часть уравнения первого закона термоди­намики ^7 = йи + рйю, должна быть известна зависимость р от V (или р от Г). В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем деления (или умножения) на интегрирующий делитель. Таким интегрирующим де­лителем для элементарного количества теплоты ад является абсолют­ная температура Т° К.

Покажем это на примере идеального газа. Имеем йд = СуйТ 4-+ рйь, или, заменив р на ЯТЬ, получим йд — Сцй.Т + ЯТймЫ.

Разделив обе части последнего уравнения на Т, находим

йх}/Т = с_ис1Т/Т + Яйи/и. (6-38)

Отсюда выражение йд/Т при обратимом изменений состояния газа есть полный дифференциал некоторой функции переменных Т и р (с_а за­висит только от температуры, а Я— величина постоянная). Клаузиус назвал эту функцию энтропией и обозначил буквой 5. Измеряется полная энтропия 5 в джоулях на градус (дж/град), а удельная энтро-ші.і я — в джоулях на килограмм на градус [дж/(кг-град)].

Таким образом, дифференциал энтропии для обратимого измене­ния состояния определяется как

(6-39)

Энтропия есть однозначная функция состояния газа, принимающая для каждого его состояния вполне определенное значение. Энтропия

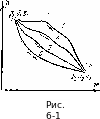является экстенсивным (зависит от массы вещества) параметром состо­яния и изменение ее в любом термо­динамическом процессе полностью оп­ределяется крайними состояниями те­ла и не зависит от пути процесса. В связи с этим энтропия газа, яв­ляясь параметром состояния, в про­цессах 1-3-2, 1-4-2, 1-5-2, 1-6-2 (рис. 6^:1) будет изменяться одина­ково. Это свойство относится как к обратимым, так и необратимым про­цессам. Поэтому

ДЯЬЗ-г = А«|-4-2 = Л$1-5-2 = = Д81.₆.8 = 5, — 5! = /(р₂0₂) — /(/>, О,).

Так как энтропия обладает свойством аддитивности, то алгебраи­ческая сумма изменений энтропии отдельных тел, составляющих тер­модинамическую систему, будет равна изменению энтропии всей тер­модинамической системы в целом. Причем изменения энтропии отдель­ных тел в зависимости от процесса могут быть как положительными, так и отрицательными величинами.

Энтропия может быть определена как функция основных парамет­ров состояния:

8 = /, (р, V); з - !_г (р, Т); ₈ = /₈ (о, Т).

Полные дифференциалы энтропии имеют вид:

(6-40)

— (дз/др)^, йр + (д8\дь)_р йи, о15 = (д51др)тйр + (дз/дТ)_ро1Т, о1з = (дз/до)_т<1о + (д8/дТ)_и(1Т.

Частные производные энтропии, входящие в эти уравнения, вы­числяются по уравнениям, которые выведены в гл. X.

Для получения изменения энтропии как функции Г и о соотноше­ние (6-38) представим в следующем виде:

<к = СгДТ/Т + ЯеЫо.

(6-41)

Интегрируя, при Со = const найдем для идеального газа

s₂ — Si == Сь In 7У7\ + R In i^i- (6-42)

Для получения изменения энтропии как функции Т и р следует из уравнения (6-41) исключить v. Из уравнения Клапейрона после диф­ференцирования получим:

ри = pdv + vdp = /W7; dü/o = dT/T — dp/p.

Подставляя значение dv/v в уравнение (6-41), имеем

' ds = с^ТУГ + RdT/T — R_r dp/p = CpdT/T — R dp/p.'

Интегрируя при c_v = const, находим

s₂ — Sj = c_p In T₂/7\ — ft In р₂/р_Р (6-43)

Для получения изменения энтропии как функции р и V следует из уравнения (6-41) исключить Т. Пользуясь тем же методом, получим

ds = Cvdvlv + Cbdplp -f R dv/v,

откуда

ds = (c_v + R) dv/v + c_vdplp = Cpdu/u + c_vdp/p. • Интегрируя, определяем

s₂—s₁ = Cp\n-?2- + c~_v]np₂/p_i; (6-44) ^vi

Учитывая, что изменение энтропии тела не зависит от характера процесса, полученные уравнения (6-42), (6-43) и (6-44) применимы как для обратимых, так и для необратимых процессов.

Из уравнения (6-39) можно получить общую формулу для опреде­ления теплоемкости.

Теплоемкость с_х любого процесса равна произведению абсолютной температуры Т на частную производную энтропии^ по температуре Т при х = const:

(6-45)

Подставив в уравнения (5-9) и (5-13) значение йа из уравнения (6-39), получим

Т<к = йи + pdv, (6-46) Тек = Л ~ vdp. (6-47)

Равенства (6-46) и (6-47) содержат только параметры состояния и их дифференциалы и носят/название термодинамических тождеств; они относятся к обратимым процессам.

Если в термодинамической системе кроме работы изменения объема совершается работа dlv, не связанная с изменением объема тела, то термодинамические тождества имеют вид

Тйа - du + pdv + й1_в; ' (6-48) Tds = di — ьйр + йК. . • (6-49)

В термодинамике- внутренняя энергия, энтальпия, энтропия, теплоемкости называются калорическими свойствами вещества, а удель­ный объем, абсолютное давление, температура — термическими свой­ствами.