2 В. В. Нащокин

353

Температуры поверхности стенки и в ее средней плоскости опреде­ляются из соотношения

ср

ср

о/_

Я_ст

-ТГНКЖ Ро).

(25-5)

Безразмерная координата хіі в'средней плоскости и на поверхности пластины становится постоянной величиной (при х = 0 х/1 = 0; при х = б хіі = 1) и поэтому отсутствует в уравнении (25-5):

а,

Ц

ср

/центр— /ср

/о + <

= Д(ВІ, Щ.

(25-6)

Количество теплоты, которое отдает (или воспринимает) пластина в окружающую среду за время т, должно равняться изменению ее внутренней энергии за период полного ее охлаждения (нагревания).

Начальная внутренняя энергия пластины, отсчитанная от внутрен­ней энергии при температуре среды, окружающей стенку, как от нуля, равна

<Э„ = 2Л*>6 (/₀ - /_ср) = 2^фб <>!, (25-7)

Количество теплоты, выделяющееся при охлаждении пластины, •определяется также безразмерными числами ЕН и Ро:

^{<У<Эо = /. (В!, Ро), (25-8)}

<Э, = ^2фб (/„ — /_ср._ст),

где (Зт — количество теплоты, переданное вокружающую среду за вре­мя т, дж; /_ср._ст — средняя температура стенки по истечении периода времени т, ° С.

/,

и на-

чальное теплосодержание известны, то легко вычисляются 4т. /_ц и

Зависимости (25-5), (25-6) и (25-8) даются в виде графиков или в виде табл. 25-1, 25-2, 25-3. (Таблицы позволяют решать задачи с боль- шей точностью.) Сначала вычисляют числа Еч и Ро, а по табл. 25-1, 25-2, 25-3 определяют ■0_ц/'в^,₁, СЬЛЬ- Так как /„

ча/

.<Эт.

1 а о л и ц а zo-z Значения д_0Т/д_г=/(В1, Ро) для неограниченной пластины

р0 ^\	0,0001	0,001	0,01	0,1	0,5	1	4	10	20	50
			-
0,02	—	1,0	0,99	0,98	0,93	0,86	0,59	0,34	0,19	0,08
0,05	—	1,0	0,99	0,98	0,89	0,79	0,46	0,23	0,12	0,05
0,1	—	1,0	0,99	0,97	0,85	0,73	0,37	0,17	0,08	0,04
0,5	—	1,0	0,99	0,92	0,69	0,51	0,17	0,06	0,03	0,01
1,0	—	1,0	0,98	0,88	0,56	0,35	0,08	0,02	0,01	0,0
2 ,	—	1,0	0,97	0,79	0,37	0,17	0,02	0,0	0,0	_
5 $	—	1,0	0,95	0,59	0,10	0,02	—	—	—	_
10	1,0	0,99	0,9	0,36	0,01	0,0	—	— <	—	—
20	1,0	0,98	0,81	0,13	0,0
50 ■•	. 1,0	0,96	0,6	0,01

§ 25-3. Цилиндр бесконечной длины

Рассмотрим охлаждение равномерно прогретого круглого цилиндра большой длины радиусом г в среде с меньшей постоянной температурой. Коэффициент теплоотдачи от поверхности цилиндра к среде не меняется во времени. Физические величины с, р и % материала цилиндра не за­висят от температуры и считаются известными. Необходимо определить: температуру поверхности, температуру на оси цилиндра и количество теплоты, отданное цилиндром в окружающую среду, для любого мо­мента времени.

Для цилиндра неограниченной длины дифференциальное уравне­ние теплопроводности удобнее отнести к цилиндрическим координатам.

При этом принято, что в начальный момент времени (т = 0) темпера­тура по всему объему цилиндра постоянна. Тогда

Задача на охлаждение цилиндра аналогична задаче на охлаждение пластины. Поэтому температуры на поверхности, на центральной оси и тепдопотери цилиндра через произвольные промежутки времени оп­ределяются из следующих соотношений:

^_ст/*1 = / (В1, Ро); = /1 (В1, Ро); = /₂ (В1, Ио). (25-10)

Для цилиндрической стенки

В1 = аг/к_ст; Ро =.ат/г²,

где г — радиус, цилиндра.

Величины ОстЯ!,, дц/*! и С?_т/<Эо определяют по табл. 25-4, 25-5, 25-6, а затем по ним легко найти /_ст, t_ц и <2_Х-

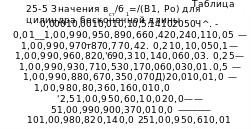Таблица 25-4 Значения ^_ц/в₁=/(В1, Ро) для цилиндра бесконечной длины

р0	0,0001	0,001	0,01	0,1	0,5	1	, 4	10	20	50
0,01			-					1,0	1,0	1,0
0,05	—	—	—	—	1,0	1,0	1,0	0,99	0,99	0,99
- 0,1	—	—	—	1,0	0,99	0,97	0,94	0,9	0,88	0,87
0,25	—	— .	1,0	0,98	0,89	0,81	0,59	0,48	0,43	0,4
0,5	—	—	0,99	0,93	0,72	0,55	0,24	0,15	0,12	0,1
1,0	■ —	■ —	0,98	0,84	0,46	0,25	0,04	0,01	0,01	0,01
2,5	—	1,0	0,95	0,63	0,12	0,02	0,0	0,0	0,00	0,00
5	1,0	0,99	0,91 '	0,38	0,01	0,0	—	—	— ■	—
10	1,0	0,98	0,82	0,14	0,0
25	1,0	0,95	0,61	0,01						—

Внутреннюю энергию рассматриваемого участка цилиндра длиной ^отсчитанную от ее значения при температуре среды, как от нуля, на­водим по формуле

(?₀ = лг²1рс% (25-11)

§ 25-4. Шар

Рассмотрим охлаждение шара радиусом г, масса* которого равно­мерно прогрета до постоянной температуры в среде с более низкой Врэстоянной- температурой. Физические постоянные с; р и Я, а также коэффициент теплоотдачи известны. Требуется определить для любого шзмента времени: температуру поверхности, температуру в центре ша­ра и количество теплоты, теряемое шаром в окружающую среду.

Дифференциальное уравнение-теплопроводности удобнее отнести ^•сферическим координатам:

•:, * _{= я} + *>\ (25-12)

'Задача на охлаждение шара аналогична задачам на охлаждение йяастины и цилиндра*; безразмерные величины Фст/¹^, Фц/'Э'! и 1р/<2₀ являются функцией только двух чисел В1 и Ро и определяются " следующих соотношений:

', в_Ст/<>1 = / (В1, Ро); = / (^В1> ^р°): <М?о-= / (В1, Ро). Щ|я шара

В1 = агА,_ст, Ро = ах/г², 111 ^г-—радиус шара.

Расчет охлаждения и нагревания тел конечных размеров приведены

Е&яебнике «Теплопередача» В. П. Исаченко, В. А, О с и п о в о й, Ец^С". С у к о м е л (М., «Энергия», 1969).

Зависимости между безразмерными величинами определяются по табл. 25-7, 25-8, 25-9 или графикам, а затем по ним — /_ст, /_ц и 0_Х.

Начальная внутренняя энергия шара отсчитывается от ее значения при температуре среды как от нул'я по формуле

<Э„ = (4/3)лг³рс (*„ - /_ср). (25-13)

Пример 25-1. Так как методика решения задач для всех рассмотрен­ных случаев одинакова, то применение таблиц достаточно пояснить на одном примере — на охлаждении цилиндра.

Определить температуру на поверхности и в центре равномерно нагретого до 927° С весьма длинного стального цилиндра диаметром 400 мм через 1,0 ч и через 0,5 ч после помещения его на воздухе, темпе­ратура которого 27° С. Коэффициент теплоотдачи от стенки цилиндра к воздуху ос = 50 вт/(м^г-град), коэффициент теплопроводности стали

Значение Q_xIQi

, Та.блица 25-9 =/ (Bl, Fo) для шара

Bi

0,0001

0,001

0,01

0,1

0,5

ю

20

50

Fo

0,01 0,05 0,1 0,25 0,5 1,0 2,5 5,0 1,0 25

0,01 0,02 0,05

0,01

0,02-

0,03

0,08

0,15

0,27

0,56

0,0

0,02

0,03

0,07

0,14

0,25

0,52

0,77

0,95

0,99

0,02 0,07 0,13 0,29 0,49 0,74 0,97 1,0 0,03 0,12 0,23 0,47 0,71 0,92 1,0

0,09

0,32

0,51

0,8

0,96

1,0

0,16

0,46

'0,66

0,9

0,99

1,0

0,22 0,53 0,71 0,92 0,99 1,0 0,27 0,57 0,75 0,91 0,99 1,0

jà, == 50 от/(м-град), теплоемкость стали с = 0,71 кдж/(кг-град), рлотность стали р =. 7900 кг/л³.

Определим температуры спустя 1 ч после помещения цилиндра на рвоздухе.

Коэффициент температуропроводности * J . а = Xjcp - 50/(710-7900) = 8,9-10~⁶ мЧсек.

|Число Био

| * Bi = ar/k_CT = (50-0,2)/50 = 0,2.

I- ' '

|;Число Фурье

^ Fo = от//-² = (8,9-10-°.3600)/0,04 = 0,8.

li­ft. По значениям Bi и Fo, по табл. 25-4 и 25-5, находим безразмерные

Егемпературы:

|fr_bI/*i = 0J4; Ф_ц/Ф, = °>⁸⁰-|: Разность температур

I . .# = /„ — г_ср = 927 — 27 = 900° С.

JC Температуры поверхности и на оси цилиндра через 1 ч: |. tt_CT = 0,74-900 = 666° С или /_ст = т>_ст + /_ст = 666 + 27 = 693° С; |, = 0,8-900 = 720° С или t_u = \ + t_cV = 720 + 27 = 747° С. |.. Потери теплоты цилиндром за 1 ч Ш ' Qt/Q₀ = / (Bi, Fo).

По табл. 25-6, Q_x/Qo = 0,23, или цилиндр потерял за 1 ч 23% от |сврей начальной внутренней энергий.

Теперь определим t_CT, /_ц и QJQo через 0,5 ч.

" Числа Био и Фурье:

Bi = 0,2; Fo = (8,9-Ю-⁶ 1800)/0,04 = 0,4.

Тогда, по таблицам, ft„/ft_l = Ô;85; ft^/fti = 0,91. Разность температур

#i = h — *ср == ⁹²⁷ — ²⁷ ~ ⁹⁰⁰° С. Температура" поверхности

ft_CI = 0,85-900 = 765° С или /_ст = ft_CT + /_ср = 765 + 27 =

= 792° С. . '

Температура на оси цилиндра

т)_ц = 0,91 -900 = 819° С или *_ц = ft_n + /_ср = 819 + + 27 = 846°С. Потери цилиндра за 0,5 ч, по таблице, QJQ₀ = 0,13.

§ 25-5. Регулярный режим теплопроводности

Охлаждение однородного, изотропного тела произвольной формы в среде с постоянной температурой и постоянным коэффициентом теп­лоотдачи на его поверхности во времени определяется дифференциаль­ным уравнением теплопроводности

dtldx = aV²t (25-14)

и граничными условиями:'

[dt/dn)_n=.₀ = —(a/À)(/_CT — /_ср),

(/)х=о = /<*, у, г)..

Решение уравнения (25-14) при /_ср = const показывает, что тем­пература в любой точке тела изменяется по экспоненциальному зако­ну .

<=оо —тл

ft = 2 ^At ^ui^e , (25-15) ;= î

где ft = t₀ — /_ср; At —постоянные, зависящие от формы тела и на­чального распределения температур; [/{ — функции координат, ха­рактеризующие изменение температуры в пространстве; /и,- — постоян­ные, представляющие собой ряд положительных возрастающих чисел (nix < т_г < т₃ < ... < т,).

Анализ уравнения (25-15) показывает, что.при малых значениях х от т = 0 до %. = x_t процесс охлаждения (нагревания) зависит от на­чальных условий охлаждения и имеет случайный характер, не свя­занный с условиями охлаждения.. Этот период охлаждения будет опре-' делиться не только первым, но-и последующими членами ряда^:(25-15). Эту стадию охлаждения называют первым периодом охлаждения, или неупорядоченным процессом.

Логарифмируя последнее уравне-ре, имеем

Г-

1п д = 1п (АЩ — тх = —тх +

+ С(х,у,г). (25-17)

'С увеличением времени т ряд быстро сходится и все члены его, 1|ме первого, стремятся к нулю. При т, превышающем некоторое оп-щеленное значение т > х_ъ начальные условия начинают играть вто-|Етепенную роль, и процесс полностью определяется только условиями Щгаждения на поверхности тела,-, его физическими свойствами, гео-£трической формой и размерами. Вторая стадия охлаждения изы­щется регулярным режимом и описы-йется первым членом ряда (25-15), т, е.

I

Из уравнения (25-17) видно, что ре-.улярный режим теплопроводности ха­рактеризуется тем, что натуральный логарифм избыточной темпера-зуры г> любой точки тела, изменяется во времени по линейному за­кону. ■

После дифференцирования обеих частей уравнения (25-17) по вре­мени получаем ■

сек

¹ *> ¹ (25-18)

т =

д дх

I

Относительная- скорость изменения температуры в единицу вре­мени в любой точке тела не зависит от координат и времени. !'. Величину т называют темпом регулярного режима и определяют га опыта. Если взять внутри тела какую-либо точку и измерять в этой [©чке температуру, то процесс охлаждения можно представить кривой |»= / (т) (рис. 25-2). Величина т, очевидно, равна тангенсу угл,а на­клона прямой к оси абсцисс:

т = (1п ^ — 1пт}₂)/(т₂ — тО. (25-19)

' Теория регулярного режима теплопроводности, разработанная $ М. Кондратьевым, применима к телам любой формы. Она позволила установить связь между темпом регулярного режима, его физическими н геометрическими величинами и внешними условиями теплообмена. Л общем случае величина т определяется из уравнения

^т С

(25-20)

1^е. величина т, характеризующая скорость охлаждения тела^ прямо пропорциональна коэффициенту теплоотдачи а (если а-не -> оо) по- ■ Шрхности тела У⁷ и обратно пропорциональна его полной теплоемкости Ж~ сру, гр — безразмерный коэффициент пропорциональности, ха-||,ктеризующий неравномерность распределения температуры в теле ^являющийся функцией числа Био. ₍

Это уравнение выражает закон сохранения энергии для охлаждаю­щегося тела в" среде с постоянной температурой. Если ф = 1, то рас­пределение температур в теле равномерно; если ф = 0, то распреде­ление температур становится наиболее неравномерным — температу-. ра поверхности равна температуре среды, а температура внутри всего тела не равна температуре поверхности.

Если коэффициент теплоотдачи а -> оо, то величина т прямо про­порциональна коэффициенту температуропроводности охлаждающе­гося тела:

т_ю = а/К, или а = Кт_х, (25-21)

где К — коэффициент пропорциональности, зависящий от геометри­ческих размеров и формы тела, м². Например, для шара .

К = (г!п)\

для цилиндра

2,405\² / п

где г — радиус; / — длина цилиндра.

На основе теории регулярного режима теплопроводности Г. М. Кон­дратьев разработал методы определения теплофизических величин а, Я и с для твердых и жидких тел. Эти методы получили широкое распро­странение в технике. Преимущество метода Кондратьева заключается в простоте проведения опытов при достаточной точности получаемых результатов.