Степень черноты полного нормального излучения для различных материалов

Наименование материала

Алюминий полированный

Бронза

Железо листовое оцинкованное блестящее

Жесть белая, старая . ■» .

Золото полированное

Латунь матовая

Медь полированная .

Никель полированный

Олово блестящее

Серебро полированное

Стальной листовой прокат

Сталь окисленная . '. . . . ... . . .

Сталь сильно окисленная

Чугунное литье

Асбестовый картон

Дерево строганое

Кирпич огнеупорный . . .

Кирпич шамотный

Кирпич красный, шероховатый

Лак черный, матовый ..... ^. .. .

Лак белый

Масляные краски различных цветов _ч. .

Сажа ламповая

Стекло

Эмаль белая

50—500	0,04-0,06
50 *	0,1
30	0,23
20	0,28
200—600	0,02—0,03
20-350	0,22
50—100	0,02
200—400	0,07—0,09
20—50	0,04—0,06
200—600 .	0,02—0,03
50	0,56
200—600	- 0,8
500	0,98
50	0..8І
. 20	0,96
20	0,8—0,9
500—1000	0,8—0,9
1000	0,75
20	. 0,88—0,93
40—100	0,96—0,98
.40—100	0,8—0,95
100 .	0.92—0,96
20—400	0,95
20—100	0,91—0,94
20	' 0,9

Так как вместо второго тела можно взять любое другое, то уравне­ние (29-9) справедливо для любых тел и является математическим вы­ражением закона Кирхгофа. • ; .

Отношение-излучательной способности тела к его поглощательной способности одинаково для всех серых тел, находящихся при одинако­вых температурах, и равно излучательной способности абсолютно черного тела при той же температуре.

Это отношение можно получить термодинамическим путем.

Пусть в замкнутой-полости находятся два тела: одно черное, а дру­гое серое. Согласно второму закону термодинамики, для соблюдения теплового равновесия необходимо, чтобы каждое теле испускало и по­глощало равные количества энергии. Невыполнение- этого условия повело бы к нарушению 'равенства температур между поверхностью полости и телами. На единицу поверхности абсолютно черного тела па­дает энергия излучения 1_а\й%, которая .целиком им поглощается, и одновременно это же количество энергии тело излучает.,Отсюда сле­дует, что./дЛЛ« = Е_а%.й% и /,х'== Е,%, так как Л_в.= 1. Единица по­верхности серого тела поглощает только часть падающей на нее энер­гии ^«?1<#Ц Если поглощательная способность тела будет равна Л*, то тело поглотит количество энергии,-равное/ДЛлЙА,, испустив такое же

количество. Энергия, излучения серого тела равна E\dk. Отсюда сле­дует, что 1_гхА\а"к = Exdk.

ПоДставляя в последнее уравнение значение I_sx для черного тела, получим закон Кирхгофа:

ЕtwAi.dk = Exdk, или Е_л = Ell Ах.

Из закона Кирхгофа следует, что если тело обладает малой погло­щательной способностью, то оно одновременно обладает и. малой излу-нательной способностью (полированные металлы). Абсолютно черное тело, обладающее максимальной поглощательной способностью, имеет и наибольшую излучательную способность.

Закон Кирхгофа остается справедливым и для монохроматического излучения. Отношение интенсивности излучения тела при определен­ной длине волны к его поглощательной способности при той,же длине волны для всех тел одно и то же, если они находятся при одинаковых температурах, и численно равно интенсивности излучения абсолютно черного тела при той же длине волны и температуре, т. е. является функцией только длинй волны и температуры:

EyJAi = hi Ах = Е_л = 1,х = / (К Т).. (29-10)

Поэтому тело, которое излучает энергию при какой-нибудь длине волны, способно поглощать ее при этой же длине волны. Если тело не поглощает энергию в какой-то части спектра, то оно в этой части спект­ра и не излучает.

Из закона Кирхгофа также следует, что степень черноты серого тела е при одной и той же температуре численно равна коэффициенту по­глощения А:

е = !J1_S\ = EIE_S — CIC_S — A.

Закон Ламберта. Энергия, излучаемая телом, распростра­няется в пространстве с.различиой интенсивностью. Закон, устанавли­вающий зависимость интенсивности излучения от направления, назы­вается законом Ламберта.

Согласно закону Ламберта количество энергии,, излучаемое эле­ментом поверхности -d-F-i в направлении элемента dF₂, пропорциональ­но произведению количества энергии, излучаемого по нормали dQ_n, на величину пространственного угла da> и cos ф, составленного направле­нием излучения с нормалью (рис. 29-3, а):

(PQq, = dQnda cos q>,

■ или •. _^; •.

d²Q_v = E_ndFyd(xi cos q>, (29-11)

где. '£„-.— энергия излучения в направлении нормали.

Следовательно, наибольшее количество энергии излучается в пер­пендикулярном направлении к поверхности излучения, т. е. прн .. if = 0. С увеличением ф количество энергии излучения уменьшается и при ф = 90° равно нулю.

Для определения величины Е_п необходимо уравнение (29-М) про­интегрировать по поверхности полусферы, лежащей над плоскостью dF_t (рис. 29-3, б).

Телесный угол da представляет собой угол, под которым из какой-либо точки dF_l видна площадка dF_% на поверхности сферы радиусом Л Отсюда следует, что

dco = dF₂/r*,

или

dw = sin ydydip,

a)
dQ„-	I' '
n	rf ^4
IF,

где ф—угол, дополнительный к углу широты; ф — угол долготы. Подставляя полученное выражение в уравнение (29-11), имеем

d?Q<p — E_ndF_x sin фйфйф-соз ф.

Проинтегрируем это выражение по всей поверхности полусферы, т. е. в пределах изменения угла ф от 0 до я/2 и угла ф от О до 2я.:

В результате интегрирования найдем энергию, излучаемую эле­ментом dF_t, в пределах полусферы, равную EdF_v Следовательно,

. . 2л л/ 2

\|>=0

, EdF_t — E_ndF_t ^ ^ sin⁽P^c0S4>'d4> = nE_ndF₁,

ф= о - •

откуда

, Е_п = Е/л — — С (Т/100)⁴ = — С₀ (Г/100)⁴.

Я л

Из последнего уравнения следует, что энергия излучения в направ­лении нормали в я раз меньше плотности интегрального полусфериче­ского излучения абсолютно черного (или серого) тела, определяемого по закону,Стефана —Больцмаиа. Поэтому уравнение закона Ламберта (29-11) принимает вид

d²Q_v = — C₍₎(T{lOQ)*d(ocos<j>dF_l. . (29-11')

■ ■ я

.Последняя формула получена для интегрального излучения эле-, мента dF_l, но она останется в силе и для монохроматического излу­чения.

Формула (29-11') является основой для расчета лучистого тепло­обмена между поверхностями конечных размеров.

Закон Ламберта полностью справедлив для абсолютно черного или Серого тела, а для тел, обладающих диффузным излучением, только в пределах ф = 0—60°. Для полированных поверхностей закон Лам* берта неприменим. . . • . .

§ 29-4. Теплообмен излучением между твердыми телами Параллельные пластины

Закон Стефана —* Больцмана позволяет определить плотность соб­ственного излучения Е_и которое возникает в поверхностном слое тела и. полностью определяется его температурой и физическими свойства­ми. Если тело участвует в теплообмене излучением с другими телами, то на рассматриваемое тело падает извне энергия излучения в коли­честве £_пад. Часть, падающей энергии излучения в количестве ЛЯ_пад телом поглощается и превращается в его внутреннюю энергию. Осталь­ная часть ^энергии излучения в количестве /?£_пад отражается от тела. Сумма собственного и отраженного излучений, испускаемых поверх­ностью данного тела, называется эффективным (фактическим) излу­чением:

^вф ~ ^еоб "Ь.^^пад ⁼ ^соб "Т"0' Л) ^пад-

Эффективное излучение зависит не только от физических свойств и температуры данного тела, но и от физических свойств, температуры и спектра излучения других окружающих тел. Кроме того, оно зависит от формы, размеров и относительного расположения тел в пространстве. Вследствие этого физические свойства эффективного и собственного излучений неодинаковы и спектры их излучения различны.

Для черного тела £_8ф = Е}^, так как для него Я_отр = 0. . Рассмотрим теплообмен излучением между двумя серыми параллель­ными пластинами, разделенными прозрачной средой. Размеры пластин значительно больше расстояния между ними, так что излучение одной из них будет полностью попадать на другую. Поверхности пластин подчиняются закону Ламберта. Обозначим: температуры пластин 7\ и 7*2, коэффициенты поглощения А± и'Л₂; собственные излучения пла­стин, определяемые по закону Стефана — Больцмана, Е_х и Е₂; эф­фективные излучения пластин £_1эф и Е_гщ коэффициенты излуче­ния Су и С₂. Полагаем, что 7\ > Т₂.

Первая пластина излучает на вторую энергию; вторая пластина часть' этой энергий поглощает, а часть отражает обратно на первую, где снова первая пластина часть поглощает и часть излучает обратно на вторую, и т. д.

Суммарный поток излучения первой пластины, состоящий из соб­ственного излучения £_х и отраженного излучения второй пластины Е_2дф, находим из уравнения

^18ф ⁼ ^1 "Ь 0 ^ 1) ^2эф- '

Агалогйчно найдем суммарное излучение второй пластины: " . ^гэф ⁼ Е_г-]г (\ — А_г) Е_1аф.

Решая эти два уравнения относительно Е_1эф и Е_2аф, получаем п _ Е₁+Е₂-Л₁Е_а . р ,Е.+Е₂-А_гЁ₁

Тепловое излучение, получаемое второй пластиной, находим из уравнения

Я — Ец>ф ^29ф*

.Подставляя значение £_19ф и Е_2эф и произведя соответствующие преобразования, получаем

АгЕ_г-А_хЁ_х А_гА,.С₃(Т./100)⁴-А_гА₂С_а(Г_а/100)« ^

Л,-т-/4₂ —/11/1₂ * ЛН-Лг—А₂ "'

ИЛИ ' '"' '•.

₌ (Г,/100)« —(7у 100)« ₌₌ ^/шбг-^доо)⁴ ' ■'■

_г А₁А_гС_а А₁А₂С_а А_уА₂С_а А 'С_г

Таким образом, тепловое излучение между параллельными поверх­ностями определяется уравнением'

^{3 = ^ор 1(77.100)* — \fJ\W\F. (29-12)}

^{где С„р = у р-—г —* приведенный коэффициент излучения. :}

Ох С% С§

Вместо С_пр в расчетах можно применять приведенную степень чер­ноты системы тел в следующем виде:

°ар ^сир¹-'«» . '

где е_прприведенная степень черноты системы: ■ '

>_Р = - ^ • (29-13)

е,. е₂ :.^:

Теплообмен излучением между телами, " .. . одно из которых _ находится внутри другого

В технике часто приходится решать задачи теплообмена изл.уче.- нием, когда одно тело находится внутри другого (рис. 29-4). Поверх- ность внутреннего тела выпуклая; внутренняя поверхность внешнего тела во.гнутая. _ . »

Обозначим величины внутреннего тела через А,, С_ь е_х, Т_и Р^ и внешнего — Л _2>. С₂, г₂, Т₂, Р₂. В отличие от теплообмена между параллельными пластинами в данном случае на внутреннее тело па­дает лишь часть ф от эффективного излучения внешнего тела. Осталь-

432 . ^Ч-

ная часть энергии излучения (1 — ср) падает на поверхность внешнего тела.

Эффективное излучение внутреннего тела состоит из собственного излучения и отраженного, полученного от внешнего тела:

Аэф = Ег?! +.(1 -Аг) _Ф£_29ф. (а)

Эффективное излучение внешнего, тела состоит из собственного из­лучения, отраженного от внутреннего тела, и отраженного собствен­ного излучения:

Величина теплообмена излучением между телами равна

Q — £.1_Эф Е,

2Эф'

Решая совместно уравнения (а) и (б) и. подставляя Е_иф и Е_2яф в последнее уравнение, получаем*

^1 ґ₂ \ с₂ с_а)

^2эф ^—'. "Ь (1 + (1 -Л₂)(1

Обозначим величину

через С

пр'

Сі Р2 \ Сз С_а I

Тогда теплообмен излучением между телами, когда одно из них .находится внутри другого, определяется уравнением

<2 = С_пр/ч Ц7У100)* - (Г₂/100)⁴1. (29-15)

Если вместо С_пр в расчете применить приведенную степень черноты системы тел, то уравнение теплообмена излучением имеет следующий вид:

_{. . ■. . см(&г-(а)']- <*-•«>}

Если поверхность Т⁷, мала по сравнению с поверхностью ^₂,то отно­шение /-у.^г приближается к нулю и С_цр = С_и а уравнение тепло-; обмена принимает вид

(29-17)

(3 = С₁Г₁[(Г₁/100Г-(^.)⁴].

*.Принято, что Ф = ЯУ^- Это можно доказать, если.рассмотреть предель­ный случай, когда Т_х = 7₂. .

Произвольно расположенные тела

Аналитический вывод уравнения теплообмена излучением между двумя произвольно расположенными телами очень сложен и может быть решен лишь для частных случаев.

Теплообмен излучением между двумя произвольными телами (рис.. 29-5) рассчитывается по формуле

с?1 С_а

ІіУ_ іооу

<2 =

соб ф^сов ф_г яг² .

^₂, (29-18)

?1

С\С_г

приведенный коэффициент излу­пи

чения данной системы тел; ^£21111^12* х

X йИ₂ — угловой коэффициент излучения. Он является геометрической характеристикой и зависит от размеров, формы обоих излуча­ющих тел и их взаимного расположения. Вычисление углового коэффициента представляет большие мате­матические трудности даже для простейших случаев, и поэтому его определяют графическим путем. При решении Технических задач угловой коэффициент обычно берут из таблиц.

§ 29-5. Экраны

В различных областях .техники довольно, часто встречаются слу­чаи, когда требуется уменьшить передачу теплоты излучением. Напри­мер, нужно оградить рабочих от действия тепловых лучей в цехах,-где имеются поверхности'с высокими температурами. В других случаях необходимо оградить деревянные части зданий от энергии излучения в целях предотвращения воспламенения; следует защищать от энергии излучения термометры, так как в противном случае они дают неверные ..показания. Поэтому всегда, когда необходимо уменьшить передачу теплоты излучением, прибегают к установке экранов. Обычно экран представляет собой тонкий металлический лист с большой отражатель­ной способностью. Температуры обеих поверхностей экрана можно считать одинаковыми.

Рассмотрим действие экрана между двумя плоскими безграничными параллельными поверхностями, причем передачей теплоты конвекцией будем пренебрегать. Поверхности стенок и экрана считаем одинаковы­ми. Температуры стенок 7\ и Т₂ поддерживаются постоянными, причем 7\ > Г₂. Допускаем, что коэффициента излучения стенок и экрана равны между собой. Тогда.приведенные коэффициенты излучения меж­ду поверхностями без экрана, между первой поверхностью и экраном, экраном и второй поверхностью равны между собой.

Тепловой поток, передаваемый от первой поверхности ко второй (без экрана), определяем из уравнения

«7о = С_рр Ц7УЮ0)* - (77100)«].

Тепловой поток, передаваемый от первой поверхности к экрану, находим по формуле

?1 = с_ар кт^ту - (г_9К/юо)<],

а от экрана ко второй поверхности — по уравнению <Ь = С_ПР Г(Г_9к/100)⁴-(Г₂/100)*]. При установившемся тепловом состоянии д± = <7₂, поэтому , ад7\/100)* - (Г_9К/100)*)'= С_пр 1(Г_9К/100)* - (Г_а/100*1,

откуда

^{^ (Г}_9К^{/100)* = \ [VI00)* + (V1 ООП 1}

' Подставляя полученную температуру экрана в любое из уравнений, получаем

' д,._а =-1-С_пр[(Г₁/100)¹-(Г₂/1001*1. - . '

Сравнивая первое и последнее уравнения, находим, что установка одного экрана при принятых условиях уменьшает теплоотдачу излу­чением в два раза:

^{<71.2 =4"<7о. (29-19) .}

Можно доказать, что установка двух экранов уменьшает тепло­отдачу втрое, установка трех экранов уменьшает теплоотдачу вчетверо и т. д. Значительный эффект уменьшения теплообмена излучением по­лучается при применении экрана из полированного металла, тогда

Я1 = ^(~)яо, (29-20)

где Спр — приведенный коэффициент излучения между поверхно­стью и экраном; С„_р — приведенный коэффициент излучения между поверхностями.

§ 29-6. Излучение газов

Излучение газообразных тел резко отличается от излучения твер­дых тел. Одноатомные и двухатомные газы обладают ничтожно ма­лой излучательной и поглощательной способностью. Эти газы считают­ся прозрачными для тепловых лучей. Трехатомные (С0₂ и Н₂0 и др.) и многоатомные газы уже обладают значительной излучательной, а следовательно, и поглощательной способностью. При высокой темпе­ратуре излучение трехатомных газов, образующихся при сгорании топлив, имеет большое значение для работы теплообменных устройств. Спектры излучения трехатомных газов в отличие от излучения серых тел имеют резко выраженный селективный (избирательный) характер. Эти газы поглощают и излучают энергию только в определенных ин­тервалах длин волн, расположенных в различных частях спектра

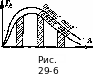(рис. 29-6). Для лучей-с другими дли­нами волн эти газы прозрачны. Когда - луч встречает на своем пути слой газа, способного к поглощению луча с данной длиной волны, то этот луч частично по­глощается, частично проходит через тол­щу газа и выходит с другой стороны слоя с интенсивностью меньшей, чем при входе. Слой очень большой тол­щины может практически поглотить луч целиком. Кроме того, поглощательная способность газа зависит от его парциального давления или числа молекулой температуры. Излу­чение и поглощение энергии в газах происходит по всему объему..

Коэффициент поглощения газа может быть определен следующей зависимостью:^- .

А% = / (Т_г, р, 5)

или общим уравнением (29-2):

= 1 —у-

Толщина слоя газа в зависит от формы тела и определяется как средняя длина луча по табл. 29-2.

Таблица 29-2