CpdT vdp , dv dp

■-L = tL или k-— — .

c_v dT * pay ' v . p

Интегрируя последнее уравнение при условии, что k — const (с_р = const и Со = const), находим

V₂ Pi

dv[v= — ^ dplp и kInvjv_x.— Inp_x/p₂. v_t pi После потенцирования имеем ■

(u₂/y_I)^fc = _Pl/p₂, или p_xv\ =.p₂v1,-откуда уравнение адиабаты

pv^k = const. (7-15)

При адиабатном процессе произведение давления на объем газа в степени k есть величина постоянная. Величину k называют показа­телем адиабаты. Рассмотрим зависимость между основными парамет­рами в адиабатном процессе.

Из уравнения адиабаты следует, что

I

Px'pt = и vJvl = {pJPiY.

Если эти соотношения параметров тела подставить в уравнение состояния для крайних точек процесса {pJPii'lpdvi) ⁼ (7V7\)> то после соответствующих преобразований найдем

k— 1

' TjT^ipJvtf-^ipJPi) ^k .

Удельная работа изменения объема / = J pdv, совершаемая те-

лом над окружающей средой при равновесном адиабатном процессе, может быть вычислена по сравнению адиабаты

Р ⁼ PiV^kJv^k

или,

I = J p_l v* (dvI v^k) = [р_г v\ I (1 — k)) (v\ - х — v} ~ ^k) =-■=

₌ Pi v\ /_1 1_Y 1 / Pi 4 Рг v'l )

k-\ \vi-¹ л-ч ^k~ⁱ Ui^_l I'

откуда

/ = (l//e - 1) (p_lVl - p₂v₂). (7-16) Из выражения (7-16) могут быть получены следующие формулы:

/ = (p_lVllk - 1) (1 - TJTy); I = (Rfk - 1) (7\ - T₂). Отношение температур заменяем отношением объемов и -давлений

/= (_Pl vjk-1) [l - (рМ~] = (RTjk-* 1) [l-ivjvj*-*].

Все зависимости между р, v, Т и уравнения работы получены при условии, что k = const. При переменной k обычно при расчетах берут среднее значение k, соответствующее изменению температуры в про­цессе по уравнению

k = c_pj I c_v j =At/A«.

Уравнения первого закона термодинамики (6-46) и (6-47) для адиа­батного процесса (dq = 0) имеют следующий вид: ■

du = —pdv udi = vdp,

откуда

(du/dv)_s = — р и (di/dp)_s = v.

Из этих соотношений можно получить

(di/du)_s =-—(v/p) (dp/dv)_s.

Полученное выражение и есть дифференциальное уравнение изо-энтропного процесса.

В этом уравнении (di/du)_s = к.

Согласно первому закону термодинамики работа изменения объема в адиабатном процессе получается за счет убыли внутренней энергии тела; при с„ — const

Если газ расширяется, то его внутренняя энергия и температура убывают; если газ сжимается, то его внутренняя энергия и темпера­тура возрастают.

Теплоемкость в адиабатном процессе из выражения с=йц1йТ при с/<7 = 0 также равна нулю.

Вычислим располагаемую (полезную) внешнюю работу в адиабат-, ном процессе, равную

р« » /' = —^ ^иФ« *

Р1

При обратимом адиабатном процессе идеального газа располагае­ма^ внешняя работа будет в к раз больше величины работы изменения объема и обратна ей по знаку.

Действительно, из уравнения адиабаты (7-15) следует, что к&иЬ — .*= — йр!р или'—ьйр — крйь, т. е. &1' = Ы1

Следовательно,

/' = _ 1) (р_Л _ р₂и₂) . (7-17)

и

V - Ы.

* Графически располагаемая внешняя работа изображается на pv-диаграмме пл. ABCD (рис. 7-5), или площадью, ограниченной линией процесса, крайними абсциссами и осью ординат.

Из рис. 7-6 видно, что поскольку в уравнении адиабаты k > 1, она на /?у-диаграмме идет круче, чем изотерма.

Для обратимого адиабатного процесса dq =- 0, поэтому

ds ' dqlT = 0hs₂ = s_± = const, (7-18)

т. е. обратимый адиабатный процесс является одновременно изоэнт-ропным (или при постоянной энтропии) и изображается в Гя-диаграмме вертикальной прямой о — Ь, параллельной оси ординат (см. рис. 7-2).

§ 7-6. Политропные процессы

До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный процесс осуществлялся при по­пето ян ном объеме; изобарный—при • постоянном давлении; изотерм-ный — при постоянной температуре; адиабатный — при отсутствии теп­лообмена между рабочим телом и внешней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки.

Условились всякий процесс идеального газа, в котором теплоем­кость является постоянной величиной, называть политропным про­цессом, а линию процесса — политропой.

Из определения политропного процесса следует, что основные тер­модинамические процессы — изохорный, изобарный, изотермический и адиабатный, если они протекают при постоянной теплоемкости, яв­ляются частными случаями политропного процесса.

Теплоемкость политропного процесса С_п может принимать самые разнообразные положительные и отрицательные значения от + оо до

— оо.

Количество теплоты, участвующее в политропном процессе, может быть выражено произведением теплоемкости процесса с_п на разность температур t₂ — t_x в конечном и начальном состояниях:

Я" = с_п (t₂ — к) ndq = с_п dt. (7-19)

Уравнение политропного процесса выводится на основании урав­нения первого закона, термодинамики:

dq = c_ndT = CpdT — vdp и dq = c^dT — c_vdT + pdv.

. Из этих уравнений найдем

(с_п — с_р)/(с_п — c_v) =■— vdplpdv.

Обозначив выражение левой части* уравнения через п, получим

(с_п — Ср)/{с_п — c_v) = п и п dvlv = —dpiр.

Интегрируя полученное соотношение в пределах от начала до кон­ца процесса, находим

п lg v₂lv_x = lg p_xlp₂

или

p_Vn = const. (7-20)

Полученное уравнение является уравнением политропнсго про­цесса.

Показатель политропы п принимает для каждого процесса опре­деленное числовое значение. Для основных процессов: изохорных п — ± со, изобарных п = 0, изотермных п = 1 и адиабатных п = k.

Поскольку уравнение политропы отличается от уравнения адиа­баты только величиной показателя п, то, очевидно, все соотношения между основными параметрами могут быть.представлены формулами, аналогичными адиабатному процессу:

п- 1

p₂/p₁ = (V^)ⁿ; T₂/T₁^(v₁/v₂r-\ т₂/т_х= (p₂/_Pl) ^п .

Теплоемкость политропного процесса определяем из формулы

п = (с_п —с_р)1 (c_n — c_v), откуда c_n = c_u l(n — k) 1(п — 1)1. (7-21)

Уравнение (7-21) позволяет определить теплоемкость политроп-■ ного процесса для каждого значения п.

Если в уравнение (7-21) подставить значения п для частных слу­чаев, то получаем теплоемкости рассмотренных процессов: изохорного процесса п = ± со, с_п = с_и; изобарного процесса п — 0, c_n = kc_v = c_v\ изотермного процесса п ~ 1, c_n = ± со; адиабатного процесса п = k, с_п = 0.

Уравнение работы изменения объема, совершаемой телом при поли-тропном процессе, имеет аналогичный вид с уравнением работы в ади­абатном процессе, т. е.

/ = tl/(n - 1)1 (р_Л - p₂v₂), (7-22)

или

п— 1

/ = \RTJn — 11 (1 — т₂/т_х) = lPaV(" — 1)1 П —.(pJPt) " ) = = - 1)1 1(1 - (vMT-¹). (7-23)

Изменение внутренней энер'гии газа и теплота в политропном про­цессе определяются по формулам:

Дм = c_v (t₂ — t_xy,

■ Q = c_n (t₂ - t_x) = c_v l(n - k)l(n - 1)1 (t₂ - h). (7-24)

Располагаемая внешняя работа в политропном процессе по анало­гии с адиабатным процессом равна

J Г = vdp = lnl{n-l)){p₁v₁-p₂v₂) = [n/(n-l))R(T₁-T₂). (7-25) pi

Изменение энтальпии в политропном процессе

' І2 — И = ^ср (*2 —

(7-26)

"Значение п в любом политропном процессе может быть определено по координатам двух любых точек графика:

(7-27)

1 =

lgl>l/t>2

-1 _JHT₂/T_t ІбРг'Рі

■ IgOz/Oi

Изображая политропный процесс в логарифмических координатах, можно предложить простой способ для определения показателя п. Логарифмируя уравнение политропы, получим

lg р + п lg v = const. .

\

Off=f

Рис. 7-8

Это уравнение представляет собой уравнение прямой линии в коор­динатах ^р и ^у, а показатель политропы я — тангенс угла наклона прямой к оси абсцисс (рис. 7-7).

Изменение энтропии газа в политропном процессе определяется по формуле

Ж = дц1Т = с_пйТ1Т, или для конечного изменения состояния

8₈-8₁ = с„1п7'₄/7'₁ = с_|,[^=^]1пГ_я/7'₁. (7-28)

Политропный процесс на Т^-диаграмме изображается (рис. 7-8) некоторой кривой, расположение которой зависит от показателя п.

На рис. 7-9 показано расположение политропных процессов на ри-диаграмме, выходящих из одной и той же точки, в зависимости от ве­личины показателя п.

Рассмотрим, как изменяется внутренняя энергия газа в политроп­ных процессах. В изотермическом процессе при п. — 1 внутренняя энер­гия газа не изменяется (и_г = и_х). В изобарном процессе расширения при п = О внутренняя энергия увеличивается. В изохорном процессе с подводом теплбт*Б1 при п — — со внутренняя энергия возрастает. От­сюда можно сделать вывод, что все политропные процессы, т. е. про­цессы расширения, расположенные над изотермой, при п<С 1, а про­цессы сжатия при п > 1 протекают с увеличением внутренней энергии газа. Политропные процессы, т. е. процессы расширения, располо­женные под изотермой, при п > 1, а процессы сжатия при /г < 1 про­текают с уменьшением внутренней энергии газа.

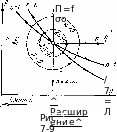Рассмотрим, как изменяется знак теплоты в политропных про­цессах (рис. 7-9). В адиабатном процессе теплота не подводится и не отводится. В изотермическом (п = 1), изобарном (п = 0) процессах расширения и в изохорном процессе (п = — со) теплота подводится. Следовательно, все политропные процессы, т. е. процессы расшире­ния, расположенные над адиаба­той в пределах к > п > — со, а процессы сжатия при со > п > & протекают с подводом теплоты к, рабочему телу.

Политропные же процессы рас­ширения при со > п > к, а процес^: сы сжатия при — со <с п <С & про-, текают с отводом теплоты.

Процессы, расположенные меж-* ду адиабатой и изотермой, имеют отрицательную теплоемкость, так как знак йцъ йи в этих процессах различный. Поскольку йи = с_ьйТ, следовательно, знак у йи соответ­ствует знаку у йТ (йи > 0, йТ > 0 и йи < 0, йТ < 0). Тогда из выражения для теплоемкости с = йа/йТ видно, что она дейст­вительно отрицательна. Практически это означает, что при подводе теплоты в этих процессах/Температура уменьшается, а при отводе теп­лоты— увеличивается.