8.1.2. Інтервальне оцінювання
Розглянемо тепер методи інтервального оцінювання. Довірчим інтервалом називається інтервал (a; b), у який із заданою ймовірністю р попадає оцінюваний параметр. Імовірність р називається довірчої. Замість неї часто задають величину α = 1 - р, називану рівнем значущості. Якщо вибірка об'єму m представляє випадкову величину, розподілену нормально, то довірчі інтервали для математичного очікування й дисперсії рівні.
де tp(n) і χр(n) - квантилы розподілу Ст’юдента та хі-квадрат, α = 1 - р.
Вертаємося на аркуш 1 електронної таблиці з даними прикладу й для них обчислимо довірчі інтервали при р=0,05. Уводимо дані згідно з малюнком:
Для обчислення величини
слугує функція «ДОВЕРИТ» категорії «Статистичні» із трьома параметрами «Альфа» - рівень значимості α = 1 – р, «Станд. откл» – середньоквадратичне відхилення (СКО) S, «Розмір» - об'єм вибірки n. Таким чином, уводимо в Н3 функцію:
=СРЗНАЧ(А1:А25)-ДОВЕРИТ(І1;СТАНДОТКЛОН(А1:А25);25)
а в комірку І3 функцію:
=СРЗНАЧ(А1:А25)+ДОВЕРИТ(І1;СТАНДОТКЛОН(А1:А25);25)
Для обчислення довірчого інтервалу для дисперсії слід зазначити, що функція обчислення квантилі розподілу хі-квадрат (зворотного розподілу хі-квадрат) називається «ХИ2ОБР» (категорія «Статистичні») і має два параметри: перший «Імовірність» містить довірчу ймовірність р, другий - ступінь свободи n–1. Уводимо відповідно до даних умов і формулою для довірчого інтервалу в комірка Н4 запис: =ДИСП(А1:А25)*24/ХИ2ОБР(0,025;24), а в комірку І4 запис: =ДИСП(А1:А25)*24/ХИ2ОБР(0,975;24). Одержуємо значення границь довірчих інтервалів.
8.2 Перевірка статистичних гіпотез про вид розподілу
Методи перевірки статистичних гіпотез займають центральне місце в дослідженнях математичної статистики. Однією з найважливіших груп критеріїв перевірки статистичних гипотез є критерії перевірки про вид розподілів (критерії згоди). Вони за вибірковим даними перевіряють припущення про приналежність генеральної сукупності до того чи іншого виду розподілів. Одним з найбільш потужних критеріїв згоди є критерій Пірсона, називаний ще критерієм хі-квадрат. Його суть полягає в порівнянні теоретичних частот елементів вибірки ni ( для дискретних розподілів) з теоретичними частотами n’i = npi, де pi - імовірність прийняти це значення, розраховане за досліджуваним законом розподілу. Якщо розподіл безперервний, то будується групований статистичний ряд з k інтервалів і Pi = F(bі) - F(ai) існує ймовірність потрапити в i-й інтервал угруповання (тут F(x) - функція розподілу закону, що перевіряється). Статистикою критерію є величина
Критичне значення критерію дорівнює зворотному розподілу хі-квадрат зі ступенями волі (k-r-1)
де r - число оцінюваних параметрів закону розподілу. Розподіл можна вважати відповідним теоретичному якщо виконується умова χ2 < χ2kr. Розглянемо розв'язок даної задачі на прикладі.
Розбір вирішення задачі
Є вибірка довгі тіла 40 особин молоди плотви, мм. Необхідно перевірити статистичну гіпотезу про те, що довга тіла молоди плотви в даній вибірці розподілена за нормальним законом розподілу. Побрати рівень значимості α=0,05 .
Вибірка довжини тіла 40 особин молоді плотви, мм:
|
|||||||||||||||||||
64 |
56 |
69 |
78 |
78 |
83 |
47 |
65 |
77 |
57 |
61 |
52 |
50 |
58 |
60 |
48 |
62 |
63 |
68 |
64 |
64 |
64 |
79 |
66 |
65 |
62 |
85 |
75 |
88 |
61 |
82 |
52 |
72 |
75 |
84 |
66 |
62 |
73 |
64 |
74 |
Для перевірки гіпотези про приналежність генеральної сукупності нормальному виду розподілів необхідно побудувати групований статистичний ряд, тому що нормальний розподіл є безперервним. Для цього потрібно знати розмах вибірки, який дорівнює різниці між максимальним і мінімальним елементами вибірки. Крім того, потрібно розрахувати крапкові оцінки математичного очікування та СКО. Відкриваємо електронну таблицю й уводимо дані вибірки в комірки А2-А41, робимо підписи для розрахункових параметрів відповідно до малюнка:
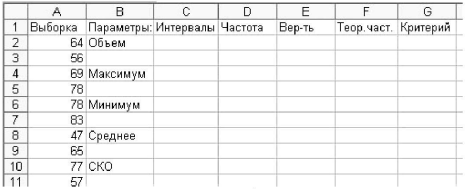
Обчислюємо параметри по вибірці. Для цього вводимо в комірку В3: =РАХУНОК(А2:А41). В В5 уводимо: =МАКС(А2:А41), в В7: =МІН(А2:А41), в В9: =СРЗНАЧ(А2:А41), в B11: =СТАНДОТКЛОН(А2:А41).
Видно, що весь діапазон значень елементів лежить на інтервалі від 47 до 88. Розіб'ємо цей інтервал на інтервали: [0; 50], (50; 55], (55; 60], (60; 65], (65; 70], (70; 75], (75; 80], (80; 85], (85; 90]. Для цього вводимо в комірки С2-С11 границі інтервалів:
Комірка |
С2 |
С3 |
С4 |
С5 |
С6 |
С7 |
С8 |
С9 |
C10 |
C11 |
Число |
0 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
Для обчислення частот n використовуємо функцію ЧАСТОТА. Для цього в D3 уводимо формулу =ЧАСТОТА(А2:А41;СЗ:З11). Потім обводимо курсором комірки D3-D11, виділяючи їх і натискаємо F2, а потім одночасно Ctrl+Shift+Enter. У результаті в комірких D3-D11 виявляться значення частот.
Для розрахунків теоретичної ймовірності pi=F(bi)-F(ai) уводимо в комірку Е3 різницю між функціями нормального розподілу (функція HOPMPАСП категорії «Статистичні») з параметрами: «X» - значення границі інтервалу, «Середнє» - посилання на комірку В9, «Стандартне відхілення» - посилання на B11, «Інтегральна» - 1. У результаті в Е3 буде формула: =HOPMPАСП(СЗ; $В$9; $В$11;1)-НОРМРАСП(З2; $В$9; $В$ 11; 1) Автозаповненням водимо цю формулу у комірки Е3-Е10 переміщаючи нижній правий кут Е3 до комірки Е10. В останньому гнізді стовпця E11 для дотримання умови нормування вводимо доповнення попередніх імовірностей до одиниці. Для цього вводимо в E11: = 1-СУМ(Е3:Е10)
Для розрахунків теоретичної частоти n’i = npi уводимо в F3 формулу: =ЕЗ*$В$3, та за допомогою автозаповнення копіюємо її на F3-F11.
Для обчислення елементів суми
критерію Пірсона вводимо в G3 значення =(D3-F3)*(D3-F3)/F3 і автозаповнюєм його на діапазон G3-G11.
Знаходимо значення критерію χ2 і критичне значення χ2kr. Для цього вводимо в F12 підпис «Сума», а в F13 підпис «Критич.». Уводимо в сусідні комірки формули - в G12: =CYMM(G3:G11), а в G13: =ХИ2ОБР(0,05;6), тут параметр α=0,05 узятий з умови, a ступінь свободи (k–r—1)=(9–2 –1)=6, тому що k=9 число інтервалів, а r=2, тому що були оцінені два параметри нормального розподілу: математичне очікування й СКО. Видно, що χ2 < χ2kr, тобто можна вважати, що довга тіла особин плотви в даній вибірці розподілена за нормальним законом розподілу.
Перевіримо це, побудувавши графіки щільностей емпіричного й теоретичного розподілів. Ставимо курсор у будь-яку вільну комірку й викликаємо майстер діаграм (Вставка/Діаграма). Вибираємо тип діаграми «Графік» і вид «Графік з маркерами» самий лівий у другому рядку, натискаємо «Далі». Ставимо курсор у поле «Діапазон» і втримуючи кнопку CTRL обводимо мишею область гнізд D3-D11 а потім F3-F11. Переходимо на закладку «Ряд» і в поле «Підпису осі X» обводимо область С3-С11. Натискаємо «Готово». Видно, що графіки досить добре збігаються, що свідчить про відповідність даних нормальному закону.