§28. Условное математическое ожидание

Важной характеристикой условного распределения вероятностей является условное математическое ожидание.

Определение. Условным математическим ожиданием дискретной случайной величины η при ξ=х (х - определенное возможное значение ξ) называют произведение возможных значений η на их условные вероятности:

M(η|ξ=х)= p(y_j|x).

Для непрерывных величин

M(η|ξ=х)= ψ(y|x)dy,

где ψ(y|x) - условная плотность случайной величины η при ξ=х.

Условное математическое ожидание M(η|х) есть функция от х:

M(η|х)=f(x),

которую называют функцией регрессии η на ξ.

Аналогично определяются условное математическое ожидание случайной величины ξ и функция регрессии ξ на η:

Пример. Дискретная двумерная случайная величина задана таблицей значений.

ξ/η	x1=1	x2=3	x3=4	x4=8
y1=3	0,15	0,06	0,25	0,04
y2=6	0,30	0,10	0,03	0,07

Найти условное математическое ожидание составляющей η при ξ=х₁=1.

Решение. Найдем р(х₁), для чего сложим вероятности, помещенные в первом столбце таблицы:

р(х₁)=0,15+0,30=0,45.

Найдем условное распределение вероятностей величины η при ξ=х₁=1:

р(у₁|х₁)=р(х₁,y₁)/p(х₁)=0,15/0,45=1/3;

р(у₂|х₁)=р(х₂,y₂)/p(х₁)=0,30/0,45=2/3.

Найдем искомое условное математическое ожидание:

M(η|ξ=х₁)= p(y_j|x₁)=у₁ р(у₁|х₁)+у₂ р(у₂|х₁)=3 (1/3)+6 (2/3)=5.

§29. Ковариация. Коэффициент корреляции

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся ковариация (корреляционный момент) и коэффициент корреляции.

Определение. Ковариацией случайных величин ξ и η называют математическое ожидание произведения отклонений этих величин:

cov(ξ,η)=М{[ξ-M(ξ)][η-M(η)]}.

Для вычисления ковариации дискретных величин используют формулу

cov(ξ,η)= х_i-М(ξ)] [y_j-M(η)]р(х_i,y_j),

а для непрерывных величин - формулу

cov(ξ,η)= [y-M(η)]f(x,y)dxdy.

Ковариация служит для характеристики связи между величинами ξ и η. Ковариация равна нулю, если ξ и η независимы; следовательно, если ковариация не равна нулю, то ξ и η - зависимые случайные величины.

Отметим, что ковариацию можно определить как математическое ожидание произведения центрированных случайных величин:

cov(ξ,η)=М[ ].

3амечание. Легко убедиться, что ковариацию можно записать в виде

cov(ξ,η)=М(ξη)-М(ξ)М(η).

Теорема. Ковариация двух независимых случайных величин ξ и η равна нулю.

Доказательство. Так как ξ и η - независимые случайные величины, то их отклонения ξ-M(ξ) и η-M(η) также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим

cov(ξ,η)=М{[ξ-M(ξ)][η-M(η)]}=M[ξ-M(ξ)]M[η-M(η)]=0.

Из определения ковариации следует, что она имеет размерность, равную произведению размерностей величин ξ и η. Другими словами, величина ковариации зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина ковариации имеет различные значения в зависимости от того, в каких единицах были измерены величины.

Пусть, например, ξ и η были измерены в сантиметрах и cov(ξ,η)=2 см²; если измерить ξ и η в миллиметрах, то cov(ξ,η)=200 мм². Такая особенность ковариации является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того чтобы устранить этот недостаток, вводят новую числовую характеристику - коэффициент корреляции.

Определение. Коэффициентом корреляции r(ξ,η) случайных величин ξ и η называют отношение ковариации к произведению средних квадратических отклонений этих величин:

r(ξ,η)=cov(ξ,η)/( ).

Так как размерность cov(ξ,η) равна произведению размерностей величин ξ и η, имеет размерность величины ξ, имеет размерность величины η, то r(ξ,η) - безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. Очевидно, коэффициент корреляции независимых случайных величин равен нулю (так как cov(ξ,η)=0).

Замечание. Во многих вопросах теории вероятностей целесообразно вместо случайной величины ξ рассматривать нормированную случайную величину ξ’, которую определяют как отношение отклонения к среднему квадратическому отклонению:

ξ’=(ξ-M(ξ))/

Нормированная величина имеет математическое ожидание, равное нулю, и дисперсию, равную единице. Действительно, используя свойства математического ожидания и дисперсии, имеем:

M(ξ’)=M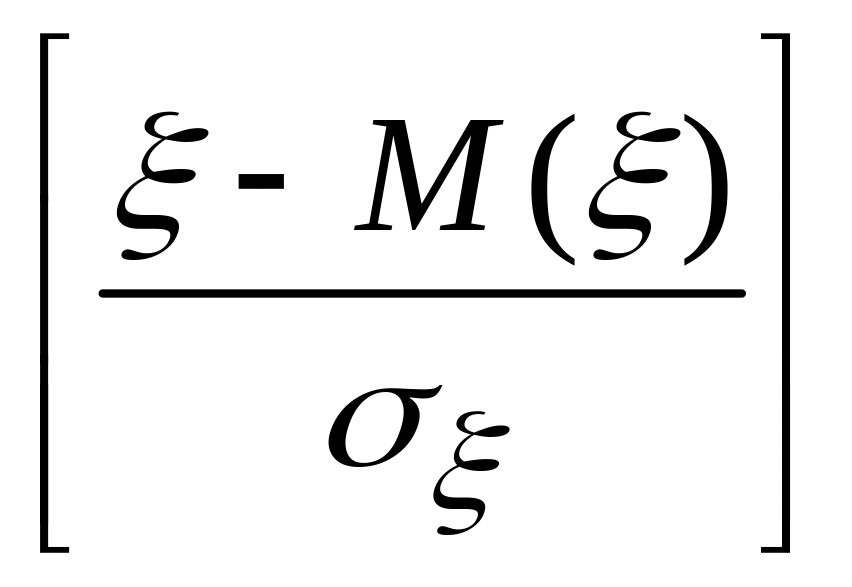 = М[ξ-M(ξ)]= 0=0;

D(ξ’)=D = D[ξ-M(ξ)]= =1.

Легко убедиться, что коэффициент корреляции r(ξ,η) равен ковариации нормированных величин ξ’ и η’:

r(ξ,η)= =M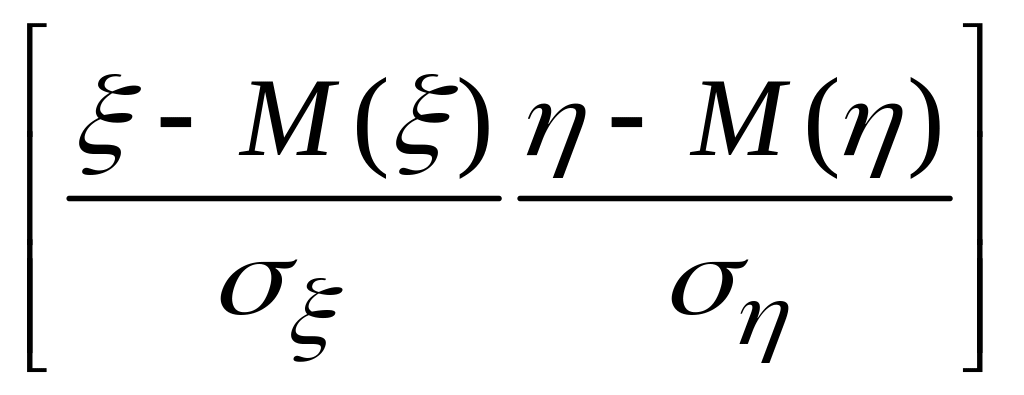 =M(ξ’η’)=cov(ξ',η’)

Теорема. Абсолютная величина ковариации двух случайных величин ξ и η не превышает среднего геометрического их дисперсий:

|cov(ξ,η)|≤

Доказательство. Введем в рассмотрение случайную величину θ₁= ξ- η и найдем ее дисперсию. Выполнив необходимые преобразования, получим

D(θ₁)=2 -2 cov(ξ,η).

Любая дисперсия неотрицательна, поэтому

2 -2 cov(ξ,η)≥0.

Отсюда

cov(ξ,η)≤ .

Введя случайную величину θ₂= ξ+ η аналогично найдем

cov(ξ,η)≥- .

Объединим неравенства

- ≤cov(ξ,η)≤ .

или

|cov(ξ,η)|≤ .

Итак,

|cov(ξ,η)|≤ .

Теорема. Абсолютная величина коэффициента корреляции не превышает единицы:

|r(ξ,η)|≤1.

Доказательство: Разделим обе части двойного неравенства

- ≤cov(ξ,η)≤ . на произведение положительных чисел .

-1≤r(ξ,η)≤1.

Итак,

|r(ξ,η)|≤1.

Определение. Две случайные величины ξ и η называют коррелированными, если их ковариация (или, что то же, коэффициент корреляции) отлична от нуля; ξ и η называют некоррелированными величинами, если их ковариация равна нулю.

Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что cov(ξ,η)=0, противоречит условию, так как для коррелированных величин cov(ξ,η)≠0.

Обратное предположение не всегда имеет место, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.

Убедимся на примере, что две зависимые величины могут быть некоррелированными.

Пример. Двумерная случайная величина (ξ,η) задана плотностью распределения:

f(x,у)=1/6π внутри эллипса x²/9+y²/4=1;

f(x,у)=0 вне этого эллипса.

Доказать, что ξ и η - зависимые некоррелированные величины.

Решение. Вычислим плотности распределения составляющих ξ и η:

f₁(x)= , f₂(у)= внутри заданного эллипса и f₁(x)=0, f₂(y)=0 вне его.

Так как f(x,у)≠f₁(x)f₂(у), то ξ и η - зависимые величины.

Для того чтобы доказать некоррелированность ξ и η, достаточно убедиться в том, что cov(ξ,η)=0. Найдем корреляционный момент по формуле

cov(ξ,η)= [y-M(η)]f(x,y)dxdy.

Поскольку функция f₁(x) симметрична относительно оси OY, то М(ξ)=0; аналогично, М(η)=0 в силу симметрии f₂(у) относительно оси OX. Следовательно,

cov(ξ,η)= yf(x,y)dxdy.

Вынося постоянный множитель f(x,у) за знак интеграла, получим

cov(ξ,η)=f(x,y) dy.

Внутренний интеграл равен нулю (подынтегральная функция нечетна, пределы интегрирования симметричны относительно начала координат), следовательно, cov(ξ,η)=0, т.е. зависимые случайные величины ξ и η некоррелированы.

Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Замечание. Теперь мы можем определить дисперсию суммы двух произвольных случайных величин

D(ξ+η)=D(ξ)+D(η)+2cov(ξ,η).

Справедливость данного соотношения вытекает непосредственно из доказательства соответствующего свойства дисперсии и определения ковариации.

На практике часто встречаются двумерные случайные величины, распределение которых нормально.

Определение. Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины (ξ,η), если

f(x,y)= × .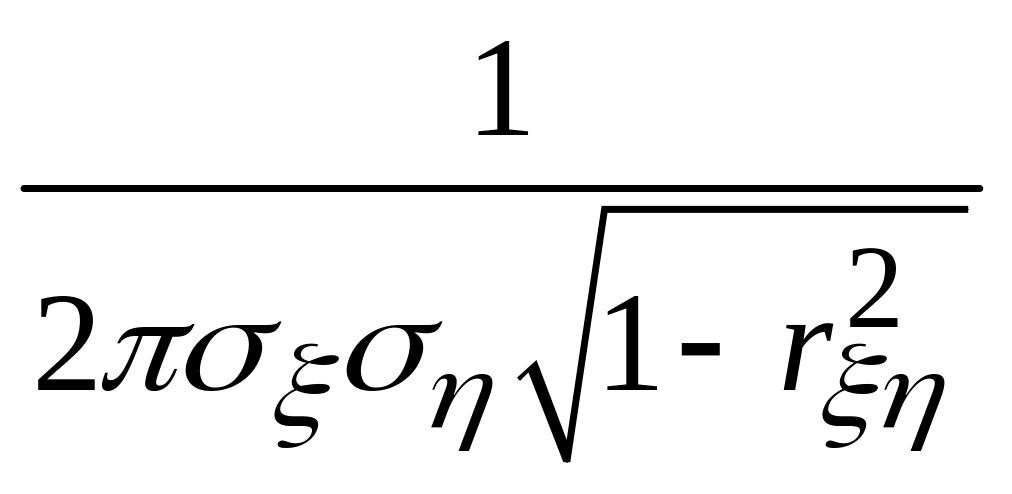

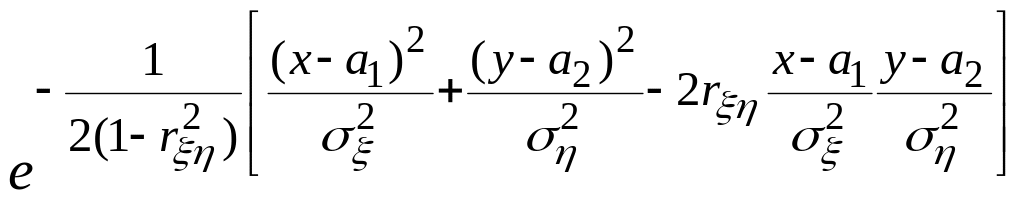Нормальный закон на плоскости определяется пятью параметрами: a₁,a₂,σ₁,σ₂ и r. Можно доказать, что эти параметры имеют следующий вероятностный смысл: a₁,a₂ - математические ожидания, σ₁,σ₂ - средние квадратические отклонения, r - коэффициент корреляции величин ξ и η.

Убедимся в том, что если составляющие двумерной нормально распределенной случайной величины некоррелированны, то они и независимы. Действительно, пусть ξ и η некоррелированны. Тогда, полагая в =0, получим

f(x,y)= × =

= =f₁(x)f₂(у).

Таким образом, если составляющие нормально распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих, а отсюда и следует независимость составляющих. Справедливо и обратное утверждение.

Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.