§26. Свойства нормального распределения

Нормальное распределение с произвольными параметрами а и σ (σ>0). называют общим, его плотность имеет вид

f(x)= e .

Определение. Нормированным называют нормальное распределение с параметрами а=0 и σ=1. Например, если ξ - нормальная величина с параметрами а и σ, то η=(ξ-а)/σ - нормированная нормальная величина, причем M(η)=0, σ(η)=l.

Плотность нормированного распределения

f₀(x)= e .

Для этой функции создана таблица значений.

Замечание. Функция F(х) общего нормального распределения

F(x)=

а функция нормированного распределения

F₀(x)= .

Для функции F₀(x) создана таблица значений. Имеет место соотношение

F(x)=F₀((x-а)/σ).

Замечание. Вероятность попадания нормированной нормальной величины ξ в интервал (0;х) можно найти, пользуясь функцией Лапласа Ф(х)= . Действительно,

P(0<ξ<x)= = =Ф(х).

Замечание. Учитывая, что =1, и, следовательно, в силу симметрии φ(x) относительно нуля =0,5, а значит, и Р(-∞<ξ<0)=0,5, легко получить, что

F₀(x)=0,5+Ф(х).

Действительно,

F₀(x)=P(-∞<ξ<x)=Р(-∞<ξ<0)+Р(0<ξ<x)=0,5+Ф(х).

Нормальная кривая.

Определение. График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Исследуем функцию

y= e

методами дифференциального исчисления.

Свойства нормальной кривой.

Свойство 1. Очевидно, функция определена на всей оси x.

Свойство 2. При всех значениях х функция принимает положительные значения, то есть нормальная кривая расположена над осью OX.

Свойство 3 Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: y=0, то есть ось OX служит горизонтальной асимптотой графика.

Свойство 4. Исследуем функцию на экстремум. Найдем первую производную:

y´= e .

Легко видеть, что у’=0 при х=а, у’>0 при х<а, у’<0 при х>а.

Следовательно, при х=а функция имеет максимум, равный 1/(σ ).

Свойство 5. Разность х-а содержится в аналитическом выражении функции в квадрате, то есть график функции симметричен относительно прямой х=а.

Свойство 6. Исследуем функцию на точки перегиба. Найдем вторую производную:

y´´= e .

Легко видеть, что при х=а+σ и х=а-σ вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 1/(σ е)). Таким образом, точки графика (а-σ,1/(σ е)) и (а+σ,1/(σ е)) являются точками перегиба.

Изобразим нормальную кривую при а=1 и σ=2.

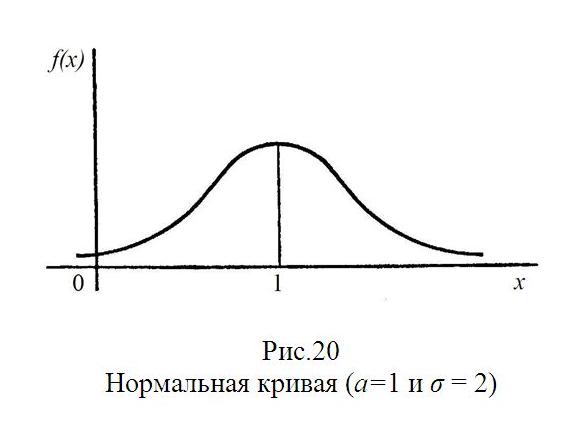
Влияние параметров нормального распределения на форму нормальной кривой.

Выясним, как влияют на форму и расположение нормальной кривой значения параметров a и σ.

Известно, что графики функций f(х) и f(x-а) имеют одинаковую форму; сдвинув график f(х) в положительном направлении оси х на а единиц масштаба при а>0 или в отрицательном направлении при а<0, получим график f(x-а). Отсюда следует, что изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси OX: вправо, если а возрастает, и влево, если а убывает.

По-иному обстоит дело, если изменяется параметр σ (среднее квадратическое отклонение). Максимум дифференциальной функции нормального распределения равен 1/(σ ). Отсюда следует, что с возрастанием σ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть сжимается к оси OX; при убывании σ нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси OY.

При любых значениях параметров а и σ площадь, ограниченная нормальной кривой и осью х, остается равной единице (по свойству плотности распределения).

Изобразим нормальные кривые при различных значениях σ и а=0. На рис.21 видно, как изменение параметра σ сказывается на форме нормальной кривой.

Заметим, что при а=0 и σ=1 нормальную кривую φ(x)= e называют нормированной.

Вероятность попадания в заданный интервал нормальной случайной величины.

Известно, что если случайная величина ξ задана плотностью распределения f(х), то вероятность того, что ξ примет значение, принадлежащее интервалу (α,β), такова:

P(α<ξ<β)= .

Пусть случайная величина ξ распределена по нормальному закону. Тогда вероятность того, что ξ примет значение, принадлежащее интервалу (α,β), равна

P(α<ξ<β)= .

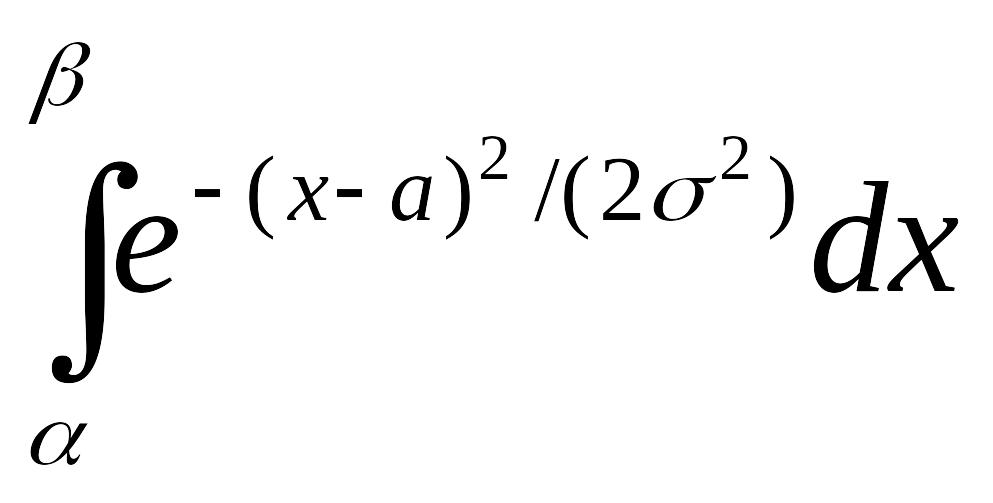Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную z=(x-а)/σ. Отсюда x=σz+a, dx=σdz. Найдем новые пределы интегрирования. Если х=а, то z=(α-а)/σ ; если х=β, то z=(β-а)/σ.

Таким образом, имеем

P(α<ξ<β)= = + =

= - .

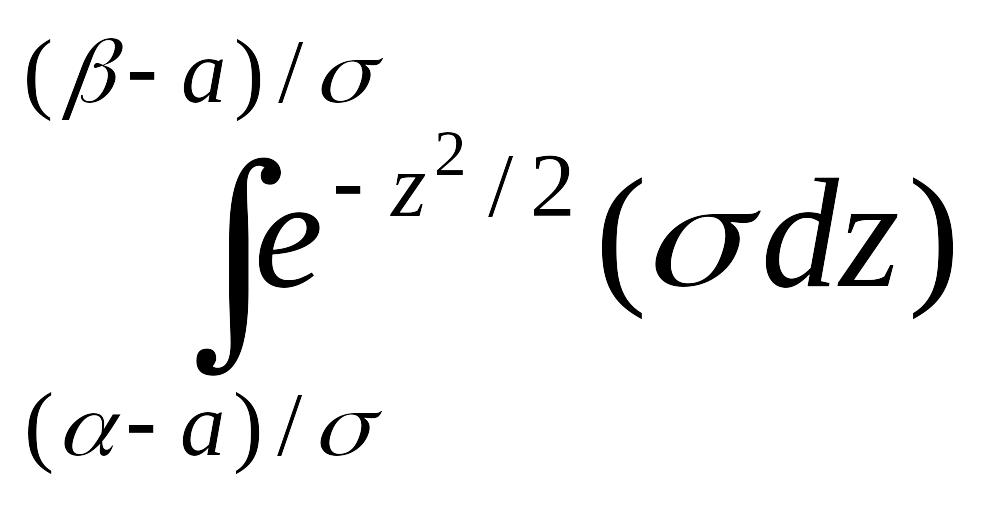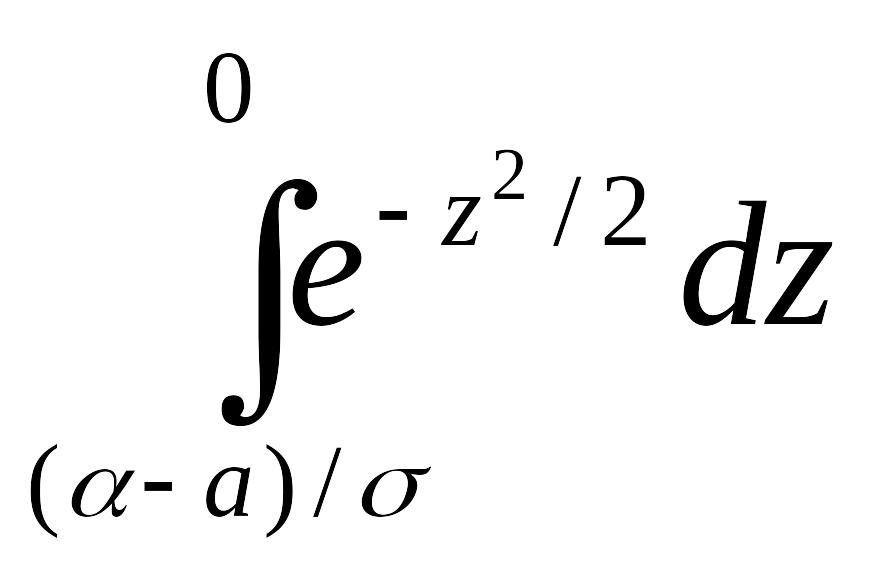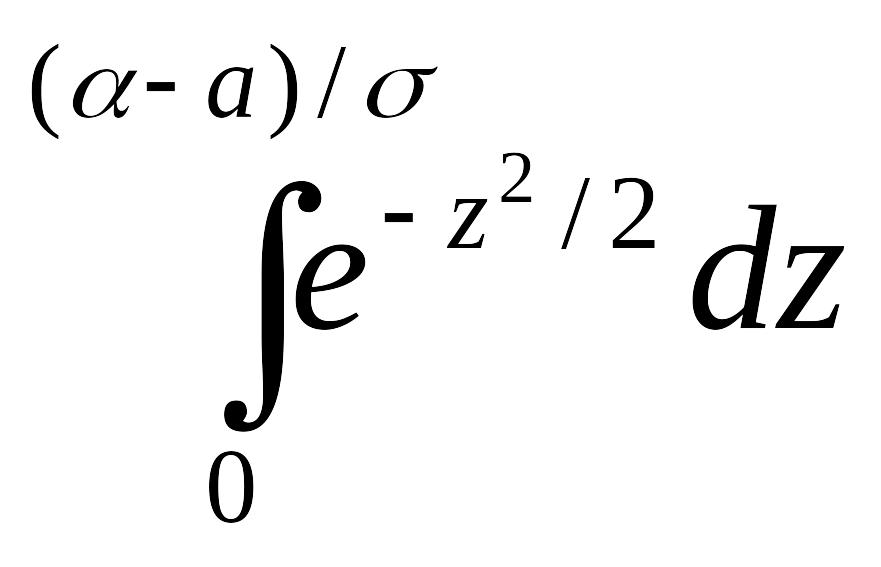Пользуясь функцией Лапласа

Ф(х)=

окончательно получим

P(α<ξ<β)=Ф -Ф .

Пример. Случайная величина ξ распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что ξ примет значение, принадлежащее интервалу (10;50).

Решение. Воспользуемся полученной формулой. По условию, α=10, β=50, а=30, σ=10, следовательно,

P(10<ξ<50)=Ф -Ф =2Ф(2).

По таблице функции Лапласа находим Ф(2)=0,4772. Отсюда искомая вероятность

Р(10<ξ<50)=2·0,4772=0,9544.

Вычисление вероятности заданного отклонения.

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины ξ по абсолютной величине меньше заданного положительного числа δ, то есть требуется найти вероятность осуществления неравенства |ξ-а|<δ.

Заменим это неравенство равносильным ему двойным неравенством

-δ<ξ-a<δ, или а-δ<ξ<а+δ. Тогда получим

Р(|ξ–а|<δ)=Р(а-δ<ξ<а+δ) =

=Ф -Ф =Ф -Ф .

Приняв во внимание равенство

Ф(-δ/σ)=-Ф(δ/σ)

(функция Лапласа - нечетная), окончательно имеем

Р(|ξ–а|<δ)=2Ф(δ/σ).

В частности, при а=0

Р(|ξ|<δ)=2Ф(δ/σ).

На рисунке наглядно показано, что если две случайные величины нормально распределены и а=0, то вероятность принять значение, принадлежащее интервалу (-δ,δ), больше у той величины, которая имеет меньшее значение σ. Этот факт полностью соответствует вероятностному смыслу параметра σ (σ есть среднее квадратическое отклонение; оно характеризует рассеяние случайной величины вокруг ее математического ожидания).

Замечание. Очевидно, события, состоящие в осуществлении неравенств |ξ–а|<δ и |ξ–а|≥δ, - противоположные. Поэтому, если вероятность осуществления неравенства |ξ–а|<δ равна р, то вероятность неравенства |ξ–а|≥δ равна 1-р.

Пример. Случайная величина ξ распределена нормально. Математическое ожидание и среднее квадратическое отклонение ξ соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение. Воспользуемся формулой

Р(|ξ–а|<δ)=2Ф(δ/σ).

По условию, δ=3, а=20, σ=10. Следовательно,

Р(|ξ-20|<3)=2Ф(3/10)=2Ф(0,3).

По таблице функции Лапласа находим Ф(0,3)=0,1179. Искомая вероятность

Р(|ξ—20|<3)=0,2358.

Правило трех сигм.

Преобразуем формулу

Р(|ξ–а|<δ)=2Ф(δ/σ),

положив δ=σt. В итоге получим

Р(|ξ–а|<σt)=2Ф(t),

Если t=3 и, следовательно, σt=3σ, то

Р(|ξ–а|<3σ)=2Ф(3)=2·0,49865=0,9973,

то есть вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.