§13. Примеры дискретных случайных величин

Биномиальное распределение.

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q=1-р). Рассмотрим в качестве дискретной случайной величины ξ число появлений события А в этих испытаниях.

Найдем закон распределения величины ξ. Для этого требуется определить возможные значения ξ и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, ..., либо п раз. Таким образом, возможные значения ξ таковы: x₁=0,x₂=1,x₃=2,...,x_n+1=п. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

P_n(k)=С p^kq^n-k ,

где k=0,1,2,...,п.

Эта формула является аналитическим выражением искомого закона распределения.

Определение. Случайная величина имеет Биномиальное распределение если ее распределение вероятностей задается формулой

P(ξ=k)=С p^kq^n-k, k=0,1,2,...,п.

Закон назван «биномиальным» потому, что правую часть формулы можно рассматривать как общий член разложения бинома Ньютона:

(p+q)ⁿ=С pⁿ+С p^n-1q+…+С p^kq^n-k+…+С qⁿ.

Таким образом, первый член разложения р^п определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член np^n-1q определяет вероятность наступления события п-1 раз; ...; последний член qⁿ определяет вероятность того, что событие не появится ни разу.

Напишем биномиальный закон в виде таблицы:

ξ	п	п-1	...	k	...	0
Р	рп	npn-1q	…	С pkqn-k	…	qn

Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины ξ - числа выпадений «герба».

Решение. Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q=1-1/2=1/2.

При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения ξ таковы: x₁=2,x₂=1,x₃=0. Найдем вероятности этих возможных значений по формуле Бернулли:

P₂(2)=С p²=(1/2)²=0,25,

P₂(1)=С pq=2·(1/2) (1/2) =0,5,

P₂(0)=С q²=(1/2)²=0,25.

Напишем искомый закон распределения:

ξ	2	1	0
р	0,25	0,5	0,25

Контроль: 0,25 + 0,5 + 0,25=1.

Распределение Пуассона.

Определение. Случайная величина имеет распределение Пуассона если ее распределение вероятностей задается формулой

P(ξ=k)= , k=0,1,2,...

Эта формула выражает закон распределения Пуассона для вероятностей редких событий. Она используется для приблизительных вычислений в схеме Бернулли, когда n велико, р мало

Имеются специальные таблицы, пользуясь которыми можно найти эти вероятности, зная k и .

Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение. По условию, п=5000, р=0,0002, k=3. Найдем :

=nр=5000·0,0002=1.

По формуле Пуассона искомая вероятность приближенно равна

Р₅₀₀₀(3)= =e^-1/3!=1/6e ≈ 0,06.

Геометрическое распределение.

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0<р<1) и, следовательно, вероятность его непоявления q=1-р. Испытания заканчиваются, как только появится событие A. Таким образом, если событие А появилось в k-м испытании, то в предшествующих k-1 испытаниях оно не появлялось.

Обозначим через ξ дискретную случайную величину - число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями ξ являются натуральные числа: x₁=1,x₂=2,...

Пусть в первых k-1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,

P(ξ=k)=q^k-1p.

Полагая k=1,2,... получим геометрическую прогрессию с первым членом р и знаменателем q (0<q<1):

p, qp, q²p, …, q^k-1p, …

По этой причине распределение называют геометрическим.

Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда будет равна

p/(1–q)=p/p=1.

Определение. Случайная величина имеет геометрическое распределение если ее распределение вероятностей задается формулой

P(ξ=k)=q^k-1p, k=1,2, ...

Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р=0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. По условию, р=0,6,q=0,4,k=3. Искомая вероятность

Р=q^k-1 р=0,4²·0,6=0,096.

Гипергеометрическое распределение.

Рассмотрим задачу. Пусть в партии из N изделий имеется М стандартных (М<N). Из партии случайно отбирают п изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь неприменима). Обозначим через ξ случайную величину - число т стандартных изделий среди п отобранных. Очевидно, возможные значения ξ таковы: 0,1,2,...,min(M, п).

Найдем вероятность того, что ξ=т, то есть что среди п отобранных изделий ровно т стандартных. Используем для этого классическое определение вероятности.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь п изделий из N изделий, то есть числу сочетаний С .

Найдем число исходов, благоприятствующих событию ξ=т (среди взятых п изделий ровно т стандартных); т стандартных изделий можно извлечь из М стандартных изделий С способами; при этом остальные п-т изделий должны быть нестандартными; взять же п-т нестандартных изделий из N-т нестандартных изделий можно C способами. Следовательно, число благоприятствующих исходов равно С C по правилу умножения.

Искомая вероятность равна отношению числа исходов, благоприятствующих событию ξ=т, к числу всех элементарных исходов

P(ξ=m)= .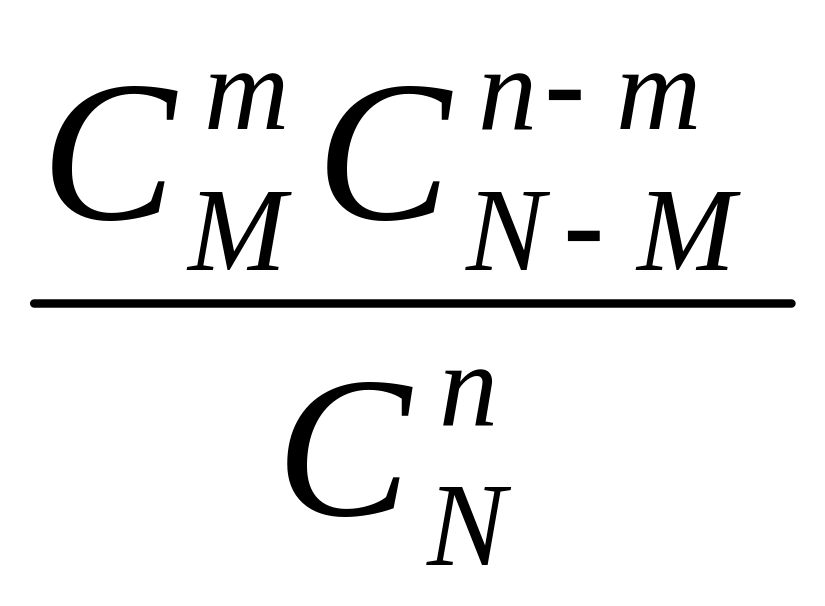

Определение. Случайная величина имеет гипергеометрическое распределение, если ее распределение вероятностей задается формулой

P(ξ=m)= .

Учитывая, что т – значение случайной величины, заключаем, что гипергеометрическое распределение определяется тремя параметрами: N,М,п. Иногда в качестве параметров этого распределения рассматривают N,n и p=M/N_, где р - вероятность того, что первое извлеченное изделие стандартное.

Заметим, что если п значительно меньше N (практически если п<0,1N), то гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.

Пример. Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наудачу извлеченных 5 изделий окажется ровно 3 окрашенных.

Решение. По условию, N=50,М=20,n=5,m=3. Искомая вероятность

P(ξ=3)=С С /С =0,234.