§14. Функция распределения случайной величины
Пусть х – действительное число. Вероятность события, состоящего в том, что ξ примет значение, меньшее х, то есть вероятность события ξ<х, обозначим через F(x). Если х изменяется, то изменяется и F(x), то есть F(x) – функция от х.
Определение. Функцией распределения случайной величины называют функцию F(x), определяющую вероятность того, что случайная величина ξ в результате испытания примет значение, меньшее х, то есть
F(x)=Р(ξ<x).
Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используют термин «интегральная функция».
Теперь можно дать более точное определение непрерывной случайной величины:
Определение. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция.
Свойства функции распределения.
Свойство 1. Значения функции распределения принадлежат отрезку [0;1]:
0≤F(x)≤l.
Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.
Свойство 2. F(х) - неубывающая функция, то есть
F (x2)≥F(х1), если х2>х1.
Доказательство. Пусть х2>х1. Событие, состоящее в том, что ξ примет значение, меньшее х2, можно подразделить на следующие два несовместных события: 1) ξ примет значение, меньшее х1, с вероятностью Р(ξ<х1) и 2) ξ примет значение, удовлетворяющее неравенству х1≤ξ<х2, с вероятностью Р(х1≤ξ<х2). По теореме сложения имеем
Р(ξ<х2)=Р(ξ<х1)+Р(х1≤ξ<х2).
Отсюда
Р(ξ<х2)-Р(ξ<х1)=Р(х1≤ξ<х2).
или
F(х2)-F(х1)=Р(х1≤ξ<х2).
Так как любая вероятность есть число неотрицательное, то F(х2)-F(х1)≥0 или F(x2)≥F(х1), что и требовалось доказать.
Следствие. Вероятность того, что случайная величина примет значение, заключенное в интервале [а;b), равна приращению функции распределения на этом интервале:
Р(a≤ξ<b)=F(b)-F(a).
Это важное следствие вытекает из предыдущего соотношения, если положить х2=b и х1=а.
Пример. Случайная величина ξ задана функцией распределения
F(х)=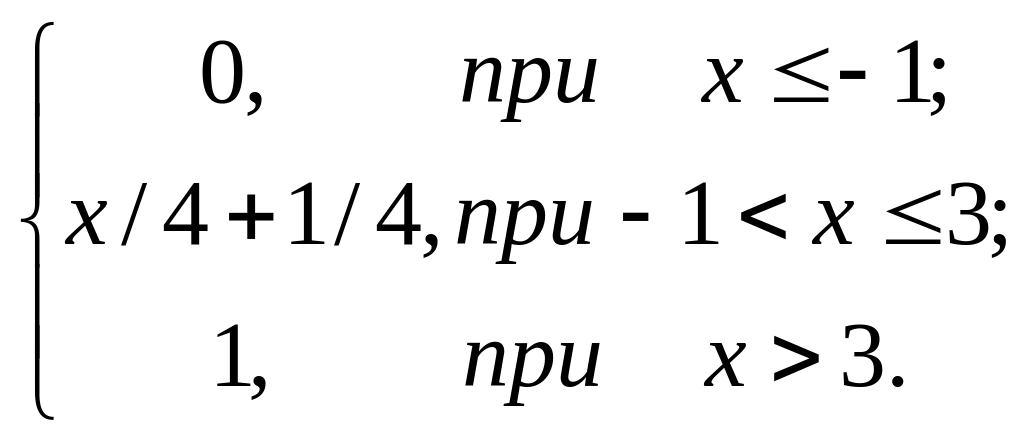
Найти вероятность того, что в результате испытания ξ примет значение, принадлежащее интервалу (0;2):
Р(0<ξ<2)=F(2)-F(0).
Решение. Так как на интервале (0;2), по условию,
F(x)=x/4+l/4,
то
F(2)-F(0)=(2/4+1/4)–(0/4+1/4)=1/2.
Итак,
Р(0<ξ<2)=1/2.
Следствие. Вероятность того, что непрерывная случайная величина ξ примет одно определенное значение, равна нулю.
Действительно, положив a=x1, b=х1+∆х, имеем
Р(х1≤ξ<х1+∆х)=F(х1+∆х)-F(х1).
Устремим ∆х к нулю. Так как ξ - непрерывная случайная величина, то функция F(х) непрерывна. В силу непрерывности F(х) в точке х1 разность F(х1+∆х)-F(х1) также стремится к нулю; следовательно, Р(ξ=х1)=0. Используя это положение, легко убедиться в справедливости равенств
Р(a≤ξ<b)=Р(a<ξ<b)=Р(a<ξ≤b)=Р(a≤ξ≤b)
Например, равенство Р(a<ξ≤b)=Р(a<ξ<b) доказывается так:
Р(a<ξ≤b)=Р(a<ξ<b)+Р(ξ=b)=Р(a<ξ<b).
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F(x)=0 при х≤а; 2) F(x)=1 при х≥b.
Доказательство. 1) Пусть х1≤а. Тогда событие ξ<х1 невозможно (так как значений, меньших х1, величина ξ по условию не принимает) и, следовательно, вероятность его равна нулю.
2) Пусть х2≥b. Тогда событие ξ<х2 достоверно (так как все возможные значения ξ меньше х2) и, следовательно, вероятность его равна единице.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
F(х)=0;
F(х)=1.
Пример. Дискретная случайная величина ξ задана таблицей распределения
ξ |
1 |
4 |
8 |
P |
0,3 |
0,1 |
0,6 |
Найти функцию распределения и вычертить ее график.
Решение. Если х<1, то F(х)=0 (третье свойство).
Если 1<х≤4, то F(x)=0,3. Действительно, ξ может принять значение 1 с вероятностью 0,3.
Если 4<х≤ 8, то F(х)=0,4. Действительно, если х1 удовлетворяет неравенству 4<х1≤8, то F(х1) равно вероятности события ξ<х1, которое может быть осуществлено, когда ξ примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события ξ<х1 равна сумме вероятностей 0,3+0,1=0,4.
Если х>8, то F(x)=l. Действительно, событие ξ≤8 достоверно, следовательно, его вероятность равна единице.
Итак, функция распределения аналитически может быть записана так:
F(х)=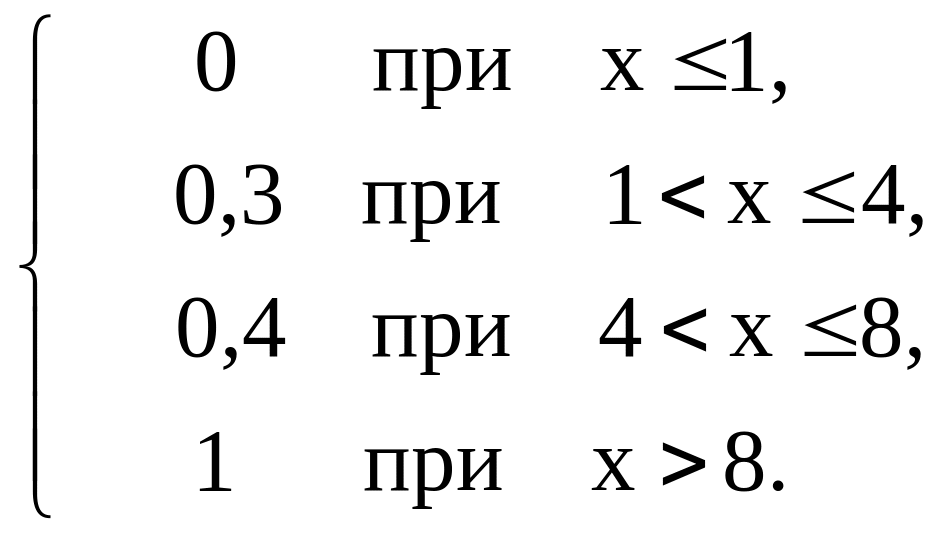
Построим график этой функции.
