§20. Условные распределения

Условные законы распределения составляющих системы дискретных случайных величин.

Если события А и В зависимы, то условная вероятность события В отличается от его безусловной вероятности. В этом случае

Р_А(В)=Р(АВ)/Р(А).

Аналогичное положение имеет место и для случайных величин. Для того чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения.

Рассмотрим дискретную двумерную случайную величину (ξ,η). Пусть возможные значения составляющих таковы: х₁,х₂,...,х_п;у₁,у₂,...,у_т.

Допустим, что в результате испытания величина η приняла значение η=у₁; при этом ξ примет одно из своих возможных значений: x₁, или х₂,..., или х_п. Обозначим условную вероятность того, что ξ примет, например, значение х₁ при условии, что η=у₁ через р(х₁|y₁). Эта вероятность, вообще говоря, не будет равна безусловной вероятности р(х₁).

В общем случае условные вероятности составляющей будем обозначать так:

р(х_i|y_j) (i=l,2,...,n; j=1,2,...,m).

Определение. Условным распределением составляющей ξ при η=у_j называют совокупность условных вероятностей р(х₁|y_j),р(х₂|y_j),...,р(х_n|y_j), вычисленных в предположении, что событие η=у_j (j имеет одно и то же значение при всех значениях ξ) уже наступило. Аналогично определяется условное распределение составляющей η.

Зная закон распределения двумерной дискретной случайной величины, можно вычислить условные законы распределения составляющих. Например, условный закон распределения ξ в предположении, что событие η=у₁ уже произошло, может быть найден по формуле

р(х_i|y₁)= (i=l,2,...,n).

В общем случае условные законы распределения составляющей ξ определяются соотношением

р(х_i|y_j)=р(х_i,y_j)/p(y_j).

Аналогично находят условные законы распределения составляющей η:

р(y_j|x_i)=р(х_i,y_j)/p(x_i).

Замечание. Сумма вероятностей условного распределения равна единице. Действительно, так как при фиксированном у_j имеем

=p(y_j), то

= /p(y_j)=p(y_j)/p(y_j)=1.

Аналогично доказывается, что при фиксированном х_i

=1.

Это свойство условных распределений используют для контроля вычислений.

Пример. Дискретная двумерная случайная величина задана таблицей.

ξ/η	x1	x2	x3
y1	0,10	0,30	0,20
y2	0,06	0,18	0,16

Найти условный закон распределения составляющей ξ при условии, что составляющая η приняла значение у₁.

Решение. Искомый закон определяется совокупностью следующих условных вероятностей:

р(х₁|y₁),р(х₂|y₁),р(х₃|y₁).

Приняв во внимание, что p(y₁)=0,10+0,30+0,20=0,60, имеем:

р(х₁|y₁)=р(х₁,y₁)/p(y₁)=0,10/0,60=1/6;

р(х₂|y₁)=р(х₂,y₁)/p(y₁)=0,30/0,60=1/2;

р(х₃|y₁)=р(х₃,y₁)/p(y₁)=0,20/0,60=1/3.

Сложив для контроля найденные условные вероятности, убедимся, что их сумма равна единице, как и должно быть: 1/6+1/2+1/3=1.

Условные законы распределения составляющих системы непрерывных случайных величин.

Пусть (ξ,η) - непрерывная двумерная случайная величина.

Определение. Условной плотностью φ(х|y) распределения составляющих ξ при данном значении η=y называют отношение плотности совместного распределения f(х,у) системы (ξ,η) к плотности распределения f₂(y) составляющей η:

φ(х|y)=f(х,у)/f₂(y).

Отличие условной плотности φ(х|y) от безусловной плотности f₁(x) состоит в том, что функция φ(х|y) дает распределение ξ при условии, что составляющая η приняла значение η=y; функция же f₁(x) дает распределение ξ независимо от того, какие из возможных значений приняла составляющая η.

Аналогично определяется условная плотность составляющей η при данном значении ξ=х:

ψ(y|x)=f(x,y)/f₁(x).

Если известна плотность совместного распределения f(x,у), то условные плотности составляющих могут быть найдены по формулам:

φ(х|y)=f(х,у)/ dx,

ψ(y|x)=f(x,y)/ dy.

Запишем представленные соотношения в виде:

f(х,у)=f₂(y)φ(х|y),f(х,у)=f₁(x)ψ(х|y).

Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин.

Как и любая плотность распределения, условные плотности обладают следующими свойствами:

φ(х|y)≥0, dx=1;

ψ(y|x)≥0, dy=1.

Пример. Двумерная случайная величина (ξ,η) задана плотностью совместного распределения

f(x,у)=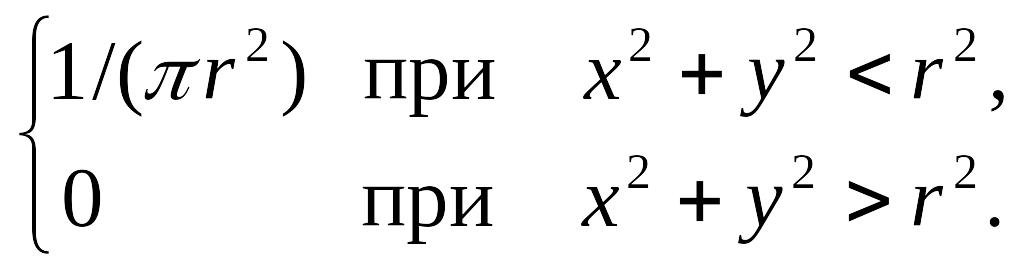

Найти условные законы распределения вероятностей составляющих.

Решение. Найдем условную плотность составляющей ξ при |x|< :

φ(х|y)= = .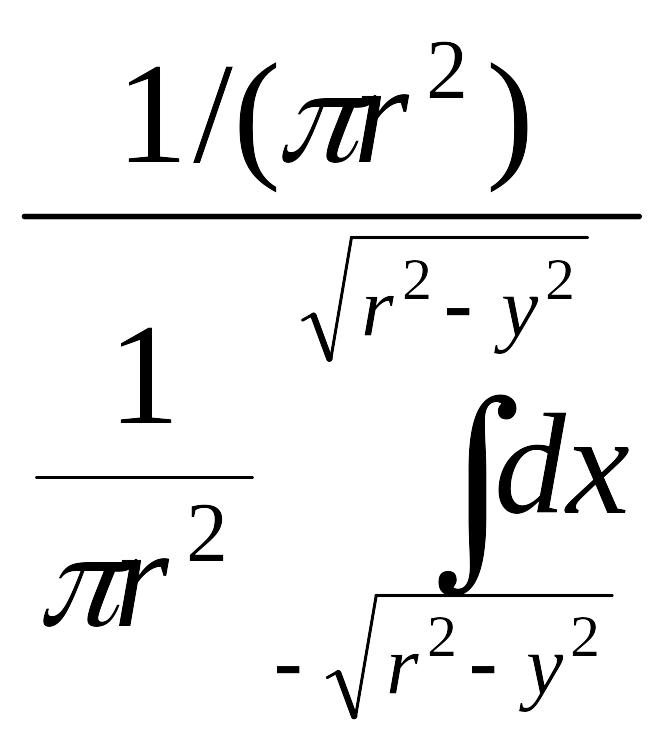

Так как f(x,у)=0 при х²+y²>r², то φ(х|y)=0 при |x|> .

Аналогично найдем условную плотность составляющей

ψ(y|x)=