§27. Функции случайных величин

Определение. Если каждому возможному значению случайной величины ξ соответствует одно возможное значение случайной величины η, то η называют функцией случайного аргумента ξ:

η=φ(ξ).

Далее показано, как найти распределение функции по известному распределению дискретного и непрерывного аргумента.

1. Пусть аргумент ξ - дискретная случайная величина.

а) Если различным возможным значениям аргумента ξ соответствуют различные возможные значения функции η, то вероятности соответствующих значений ξ и η между собой равны.

Пример. Дискретная случайная величина ξ задана распределением

ξ	2	3
P	0,6	0,4

Найти распределение функции η=ξ².

Решение. Найдем возможные значения η: у₁=2²=4;у₂=3²=9. Напишем искомое распределение η:

η	4	9
P	0,6	0,4

б) Если различным возможным значениям ξ соответствуют значения η, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений η.

2. Пусть аргумент ξ - непрерывная случайная величина. Найдем распределение функции η=φ(ξ), зная плотность распределения случайного аргумента ξ. Доказано: если у=φ(х) - дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой х=ψ(у), то плотность распределения g(y) случайной величины η находится с помощью равенства

g(y)=f[ψ(у)] |ψ´(у)|.

Пример. Случайная величина ξ распределена нормально, причем ее математическое ожидание а=0. Найти распределение функции η=ξ³.

Решение. Так как функция у=х³ дифференцируема и строго возрастает, то можно применить формулу

g(y)=f[ψ(у)] |ψ´(у)|.

Найдем функцию, обратную функции у=х³:

ψ(у)=х=y^1/3.

Найдем f[ψ(у)]. По условию,

f(x)= ,

поэтому

f[ψ(у)]=f[y^1/3]= .

Найдем производную обратной функции по у:

ψ´(у)=(y^1/3)´= .

Найдем искомую плотность распределения:

g(y)= .

Пользуясь данным соотношением можно доказать, что линейная функция η=Aξ+B нормально распределенного аргумента ξ также распределена нормально, причем для того чтобы найти математическое ожидание η, надо в выражение функции подставить вместо аргумента ξ его математическое ожидание а:

М(η)=Аа+В;

для того чтобы найти среднее квадратическое отклонение η, надо среднее квадратическое отклонение аргумента ξ умножить на модуль коэффициента при ξ:

σ(η)=|A|σ(ξ).

Математическое ожидание функции одного случайного аргумента.

Задана функция η=φ(ξ) случайного аргумента ξ. Требуется найти математическое ожидание этой функции, зная закон распределения аргумента.

1. Пусть аргумент ξ - дискретная случайная величина с возможными значениями х₁,х₂,...,х_п, вероятности которых соответственно равны р₁,р₂,...,р_п. Очевидно, η - также дискретная случайная величина с возможными значениями у₁=φ(х₁),у₂ =φ(х₂),…,у_n=φ(х_n). Так как событие «величина ξ приняла значение х_i» влечет за собой событие «величина η приняла значение φ(х_i)», то вероятности возможных значений η соответственно равны р₁,р₂,...,р_п. Следовательно, математическое ожидание функции

М[φ(ξ)]= p_i.

Пример. Дискретная случайная величина ξ задана распределением

ξ	1	3	5
P	0,2	0,5	0,3

Найти математическое ожидание функции η=φ(ξ)=ξ²+1.

Решение. Найдем возможные значения η:

φ(1)=1²+1=2; φ(3)=3²+1=10;

φ(5)=5²+1=26.

Искомое математическое ожидание функции η равно

М[ξ²+1]=2·0,2+10·0,5+26·0,3=13,2.

2. Пусть аргумент ξ - непрерывная случайная величина, заданная плотностью распределения f(x). Для отыскания математического ожидания функции η=φ(ξ) можно сначала найти плотность распределения g(y) величины η, а затем воспользоваться формулой

M(η)= g(y)dy.

Однако, если отыскание функции g(y) является затруднительным, то можно непосредственно найти математическое ожидание функции φ(ξ) по формуле

М[φ(ξ)]= f(x)dx.

В частности, если возможные значения ξ принадлежат интервалу (а, b), то

М[φ(ξ)]= f(x)dx.

Опуская доказательство, заметим, что оно аналогично дискретному случаю, если заменить суммирование интегрированием, а вероятность - элементом вероятности f (х)∆х.

Пример. Непрерывная случайная величина ξ задана плотностью распределения f(x)=sinx в интервале (0;π/2); вне этого интервала f(x)=0. Найти математическое ожидание функции η=φ(ξ)=ξ².

Решение. По условию, f(x)=sinx, φ(ξ)=х², а=0, b=π/2. Следовательно,

М[φ(ξ)]= sinxdx.

Интегрируя по частям, получим искомое математическое ожидание

М[ξ²]=π-2.

Функция двух случайных аргументов.

Определение. Если каждой паре возможных значений случайных величин ξ и η соответствует одно возможное значение случайной величины θ, то θ называют функцией двух случайных аргументов ξ и η:

θ=φ(ξ,η).

Необходимо найти распределение функции θ=ξ+η по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если ξ - погрешность показаний измерительного прибора (распределена нормально), η - погрешность округления показаний до ближайшего деления шкалы (распределена равномерно), то возникает задача - найти закон распределения суммы погрешностей θ=ξ+η.

1. Пусть ξ и η - дискретные независимые случайные величины. Для того, чтобы составить закон распределения функции θ=ξ+η, надо найти все возможные значения θ и их вероятности.

Пример. Дискретные независимые случайные величины заданы распределениями:

ξ	1	2		η	3	4
P	0,4	0,6		P	0,2	0,8

Составить распределение случайной величины θ=ξ+η.

Решение. Возможные значения θ есть суммы каждого возможного значения ξ со всеми возможными значениями η:

z₁=1+3=4; z₂=1+4=5; z₃=2+3=5; z₄=2+4=6.

Найдем вероятности этих возможных значений. Для того чтобы θ=4, достаточно, чтобы величина ξ приняла значение х₁=1 и величина η - значение y₁=3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,4 и 0,2.

Аргументы ξ и η независимы, поэтому события ξ=1 и η=3 независимы и, следовательно, вероятность их совместного наступления (то есть вероятность события θ=1+3=4) по теореме умножения равна 0,4·0,2=0,08.

Аналогично найдем:

P(θ=1+4=5)=0,4·0,8=0,32;

P(θ=2+3=5)=0,6·0,2=0,12;

P(θ=2+4=6)=0,6·0,8=0,48.

Напишем искомое распределение, сложив предварительно вероятности несовместных событий θ=z₂, θ=z₃, (0,32+0,12=0,44):

θ	4	5	6
P	0,08	0,44	0,48

Контроль: 0,08+0,44+0,48=1.

2. Пусть ξ и η - непрерывные случайные величины. Доказано: если ξ и η независимы, то плотность распределения g(z) суммы θ=ξ+η (при условии, что плотность хотя бы одного из аргументов задана на интервале (-∞,∞) одной формулой) может быть найдена с помощью равенства

g(z)= f₂(z-x)dx,

либо с помощью равносильного равенства

g(z)= f₂(y)dy,

где f₁, f₂ - плотности распределения аргументов.

Если возможные значения аргументов неотрицательны, то g(z) находят по формуле

g(z)= f₂(z-x)dx,

либо по равносильной формуле

g(z)=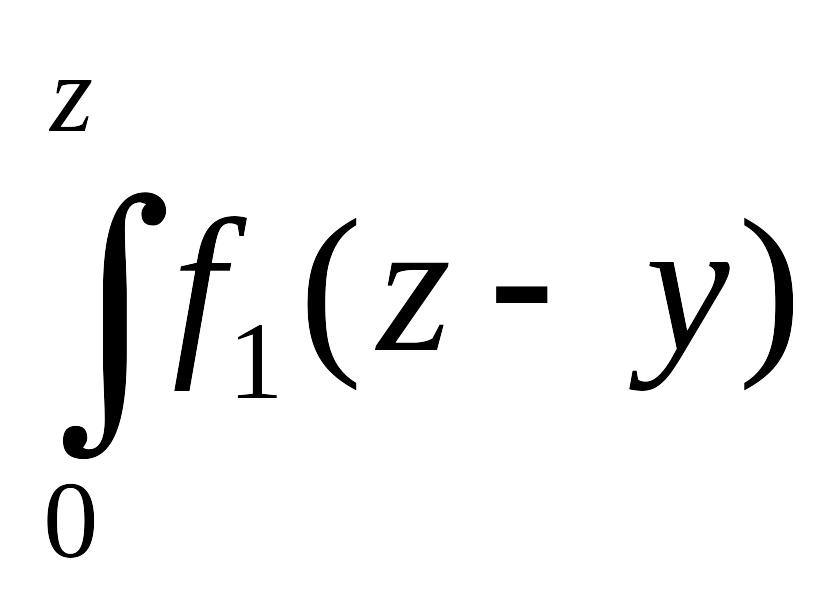 f₂(y)dy.

Определение. Плотность распределения суммы независимых случайных величин называют композицией.

Определение. Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся, вообще говоря, параметрами).

Нормальный закон обладает свойством устойчивости: композиция нормальных законов также имеет нормальное распределение (математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых). Например, если ξ и η - независимые случайные величины, распределенные нормально с математическими ожиданиями и дисперсиями, соответственно равными а₁=3, а₂=4, D₁=l, D₂=0,5, то композиция этих величин (то есть плотность вероятности суммы θ=ξ+η) также распределена нормально, причем математическое ожидание и дисперсия композиции соответственно равны а=3+4=7; D=l+0,5=1,5.

Пример. Независимые случайные величины ξ и η заданы плотностями распределений:

f(x)= e^-x/3 (0≤x<∞);

f(y)= e^-y/4 (0≤y<∞).

Найти композицию этих законов, то есть плотность распределения случайной величины θ=ξ+η.

Решение. Возможные значения аргументов неотрицательны, поэтому

g(z)= f₂(z-x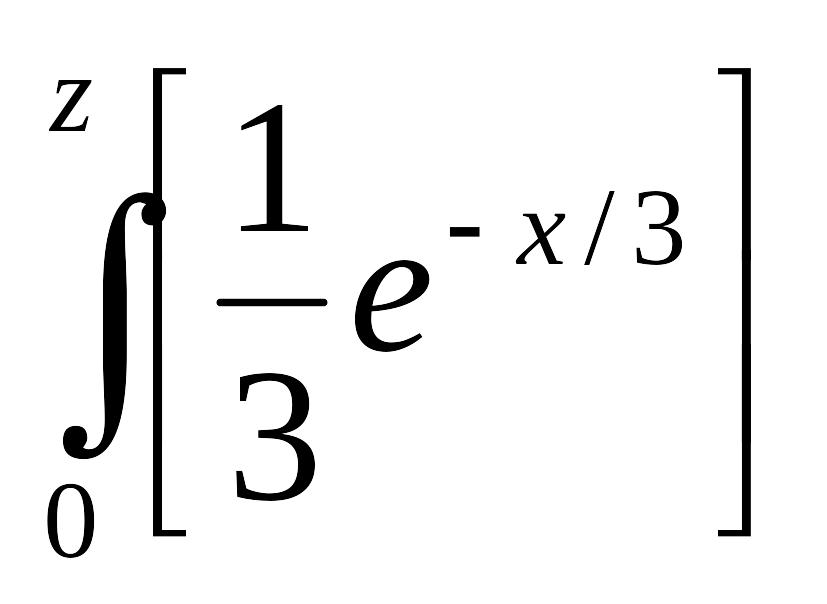)dx= dx= e^-z/4 dx=e^-z/4(1-e^-z/12).

Здесь z≥0, так как θ=ξ+η и, по условию, возможные значения ξ и η неотрицательны и имеет место равенство

dz=1.