§19. Двумерная плотность

Двумерная случайная величина задается с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Будем предполагать, что функция распределения F(х,у) всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка.

Определение. Плотностью совместного распределения вероятностей f(x,у) двумерной непрерывной случайной величины (ξ,η) называют вторую смешанную частную производную от функции распределения:

f(x,у)= .

Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.

Пример. Найти плотность совместного распределения f(x,у) системы случайных величин (ξ,η) по известной функции распределения

F(х,у)=sinх sinу (0≤х≤π/2, 0≤у≤π/2).

Решение. По определению плотности совместного распределения,

f(x,у)= .

Найдем частную производную по х от функции распределения:

=cosх sinу.

Найдем от полученного результата частную производную по у, в итоге получим искомую плотность совместного распределения:

f(x,у)= =cosх cosу (0≤х≤π/2, 0≤у≤π/2).

Нахождение функции распределения системы по известной плотности распределения.

Зная плотность совместного распределения f(x,у), можно найти функцию распределения F(х,у) по формуле

F(х,у)= dx dy,

что непосредственно следует из определения плотности распределения двумерной непрерывной случайной величины (ξ,η).

Пример. Найти функцию распределения двумерной случайной величины по данной плотности совместного распределения

f(x,у)= .

Решение. Воспользуемся формулой

F(х,у)= dx dy.

Положив f(x,у)= , получим

F(х,у)= dy= dy=

= = .

Вероятностный смысл двумерной плотности вероятности.

Вероятность попадания случайной точки (ξ,η) в прямоугольник ABCD равна

Р(х₁<ξ<х₂,y₁<η<y₂)=[F(х₂,y₂)-F(х₁,y₂)]–[F(х₂,y₁)-F(х₁,y₁)].

Обозначив для краткости левую часть равенства через Р_ABCD и применив к правой части теорему Лагранжа, получим

Р_ABCD = F (X,Y)∆x∆y,

где

х₁<X<x₂,∆x=x₂–x₁;у₁<Y<y₂,∆y=y₂–y₁.

Отсюда

F (X,Y)= ,

или

f(X,Y)= .

Приняв во внимание, что произведение ∆x∆y равно площади прямоугольника ABCD, заключаем: f(X,Y) есть отношение вероятности попадания случайной точки в прямоугольник ABCD к площади этого прямоугольника.

Перейдем теперь к пределу при ∆x→0 и ∆y→0. Тогда X→x, Y→y и, следовательно, f(X,Y)→ f(x,у).

Итак, функцию f(x,у) можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник (со сторонами ∆х и ∆у) к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к нулю.

Вероятность попадания случайной точки в произвольную область.

Запишем:

f(X,Y)∆x∆y=Р_ABCD.

Отсюда заключаем: произведение f(X,Y)∆x∆y есть вероятность попадания случайной точки в прямоугольник со сторонами ∆х и ∆у.

Пусть в плоскости XOY задана произвольная область D. Обозначим событие, состоящее в попадании случайной точки в эту область, так: (ξ,η) D.

Разобьем область D на п элементарных областей прямыми, параллельными оси OY, находящимися на расстоянии ∆х одна от другой, и прямыми, параллельными оси OX, находящимися на расстоянии ∆y одна от другой (для простоты предположим, что эти прямые пересекают контур области не более чем в двух точках). Так как события, состоящие в попадании случайной точки в элементарные области, несовместны, то вероятность попадания в область D приближенно (сумма элементарных областей приближенно равна области D) равна сумме вероятностей попаданий точки в элементарные области:

P((ξ,η) D)≈ ∆x∆y.

Переходя к пределу при ∆x→0 и ∆y→0, получим

P((ξ,η) D)= dx dy.

Итак, для того чтобы вычислить вероятность попадания случайной точки (ξ,η) в область D, достаточно найти двойной интеграл по области D от функции f(x,у).

Геометрически это равенство можно истолковать так: вероятность попадания случайной точки (ξ,η) в область D равна объему тела, ограниченного сверху поверхностью z=f(x,у), основанием которого служит проекция этой поверхности на плоскость XOY.

Пример. Плотность распределения двумерной случайной величины

f(x,у)= .

Найти вероятность попадания случайной точки в прямоугольник с вершинами К(1;1), L( ;l), M(1;0) и N( ;0).

Решение. Искомая вероятность

P((ξ,η) D)= dxdy= dy=

= arctg x = arctg y = = .

Свойства двумерной плотности вероятности.

Свойство 1. Двумерная плотность вероятности неотрицательна:

f(x,y)≥0.

Доказательство. Вероятность попадания случайной точки в прямоугольник со сторонами ∆х и ∆у есть неотрицательное число; площадь этого прямоугольника - положительное число. Следовательно, отношение этих двух чисел, а значит, и их предел (при ∆x→0 и ∆y→0), который равен f(x,y), есть неотрицательное число, т.е.

f(x,y)≥0.

Свойство непосредственно следует из того, что F(x,у) - неубывающая функция своих аргументов.

Свойство 2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:

dx dy=1.

Доказательство. Бесконечные пределы интегрирования указывают, что областью интегрирования служит вся плоскость х0у; поскольку событие, состоящее в том, что случайная точка попадет при испытании на плоскость х0у, достоверно, то вероятность этого события (она и определяется двойным несобственным интегралом от двумерной плотности) равна единице, т. е.

dx dy=1.

Пример. Задана плотность совместного распределения непрерывной двумерной случайной величины (ξ,η): f(х,у)=Сcosxcosу в квадрате (0≤х≤π/2, 0≤у≤π/2; вне этого квадрата f(х,у)=0). Найти постоянный параметр С.

Решение. Воспользуемся свойством 2, учитывая, что х и у изменяются от 0 до π/2:

C dx dy=1.

Отсюда

С= .

Выполнив интегрирование, получим искомое значение параметра С=1.

Отыскание плотностей вероятности составляющих двумерной случайной величины.

Пусть известна плотность совместного распределения вероятностей системы двух случайных величин. Найдем плотности распределения каждой из составляющих.

Найдем сначала плотность распределения составляющей ξ. Обозначим через F₁(x) функцию распределения составляющей ξ. По определению плотности распределения одномерной случайной величины,

f₁(х)= .

Приняв во внимание соотношения

F(x,у)= dx dy,

F₁(x)=F(x,∞),

найдем

F₁(x)= dx dy.

Продифференцировав обе части этого равенства по х, получим

= dу,

или

f₁(х)= dу.

Аналогично находится плотность распределения составляющей η:

f₂(у)= dх.

Итак, плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей.

Пример. Двумерная случайная величина (ξ,η) задана плотностью совместного распределения

f(x,у)=

Найти плотности распределения составляющих ξ и η.

Решение. Найдем плотность распределения составляющей ξ

f₁(х)= = = .

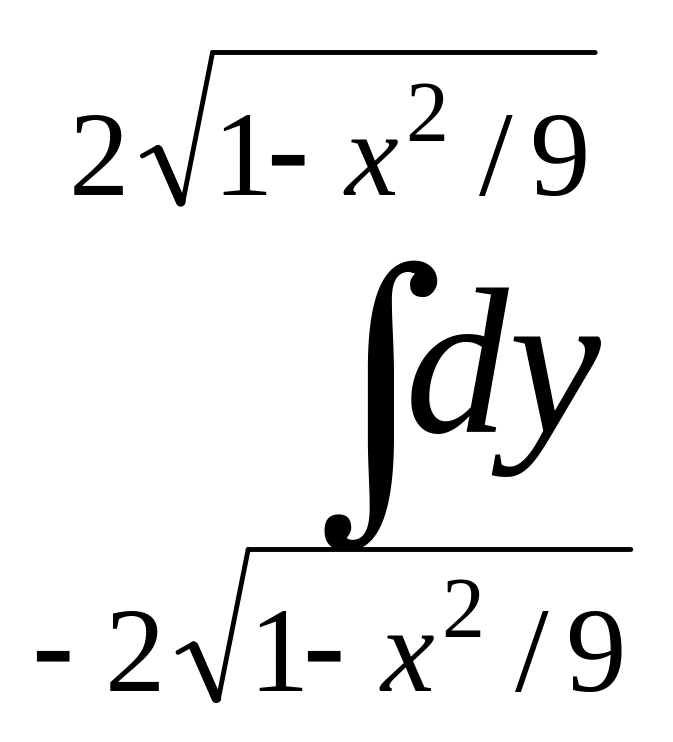Итак,

f₁(x)=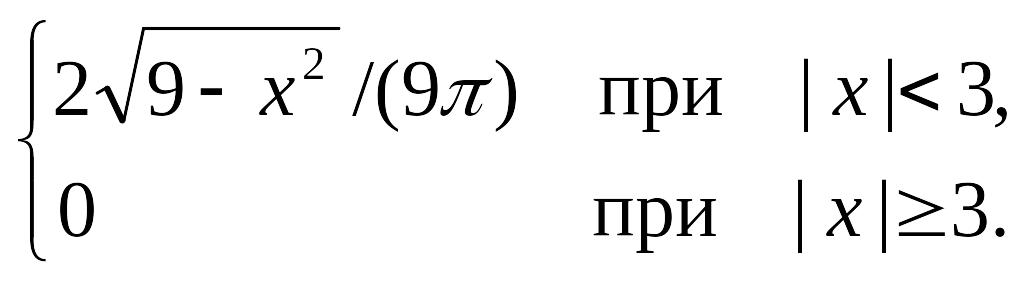

Аналогично найдем плотность распределения составляющей η:

f₂(у)=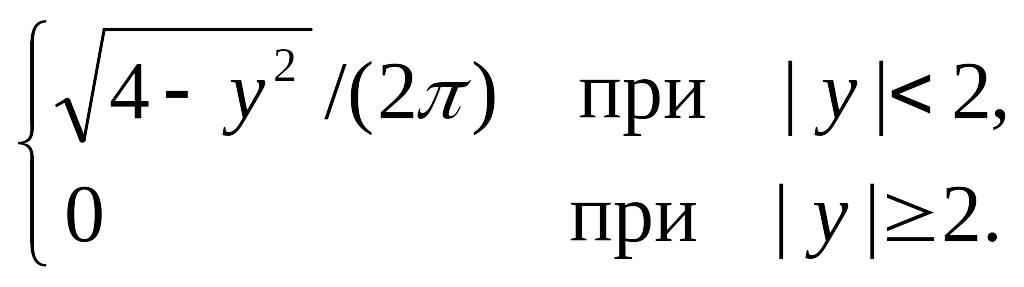

Найденные функции удовлетворяют соотношениям

dх=1 и dу=1.