§16. Примеры непрерывных распределений

Равномерное распределение.

При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений. Рассмотрим закон равномерного распределения вероятностей.

Определение. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Приведем пример равномерно распределенной непрерывной случайной величины.

Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину ξ, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, ξ имеет равномерное распределение.

Найдем плотность равномерного распределения f(x), считая, что все возможные значения случайной величины заключены в интервале (а,b), на котором функция f(х) сохраняет постоянные значения.

По условию, ξ не принимает значений вне интервала (а,b), поэтому f(х)=0 при х<а и х>b.

Найдем постоянную С. Так как все возможные значения случайной величины принадлежат интервалу (а,b), то должно выполняться соотношение

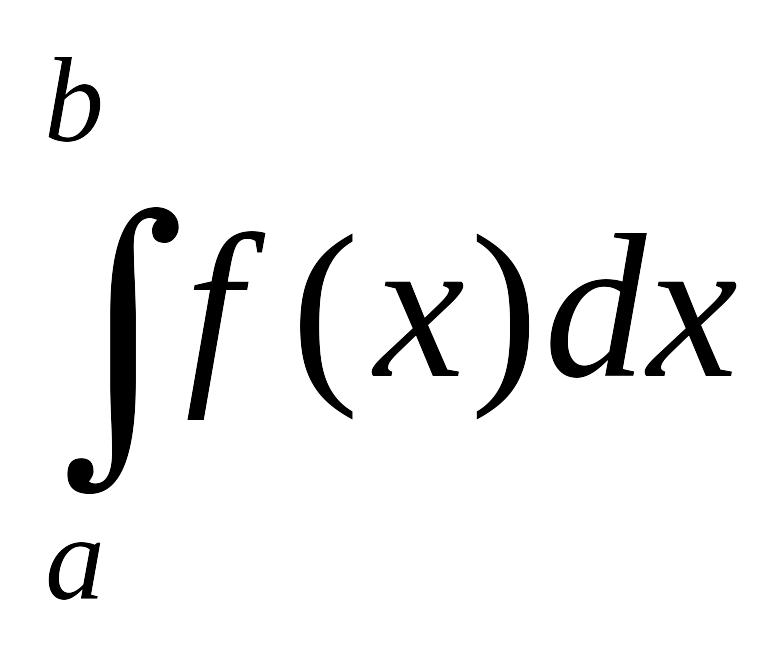=1, или =1.

Отсюда

C=1/ =1/(b-a).

Итак, искомая плотность вероятности равномерного распределения

f(х)=

Построим график плотности равномерного распределения:

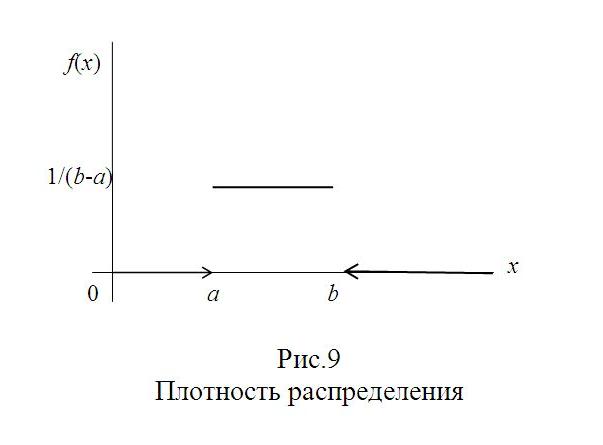
Замечание. Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале (0;1), а через r - ее возможные значения. Вероятность попадания величины R (в результате испытания) в интервал (с,d), принадлежащий интервалу (0;1), равна его длине:

Р(с<R<d)=d-c.

Действительно, плотность рассматриваемого равномерного распределения

f(r)=1/(1-0)=1.

Следовательно, вероятность попадания случайной величины R в интервал (с,d)

Р(с<R<d)= = =d–c.

Показательное распределение.

Определение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины ξ, которое описывается плотностью

f(x)=

где λ - постоянная положительная величина.

Показательное распределение определяется одним параметром λ. Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и так далее. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.

Найдем функцию распределения показательного закона

F(x)= = +λ =1-e^-λx.

Итак,

F(x)=

Мы определили показательный закон с помощью плотности распределения; ясно, что его можно определить, используя функцию распределения.

Изобразим графики плотности и функции распределения показательного закона.

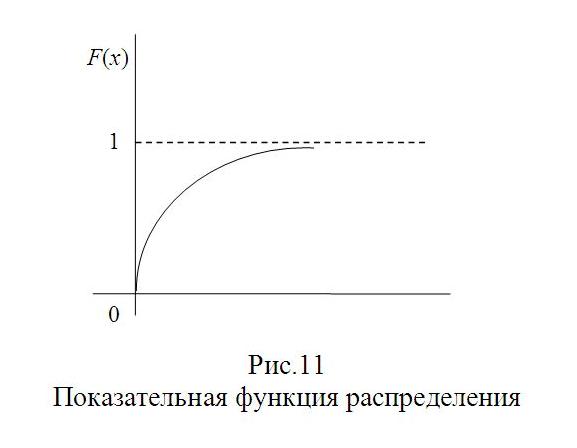
Пример. Написать плотность и функцию распределения показательного закона, если параметр λ=8.

Решение. Очевидно, искомая плотность распределения

f(x)=8e^-8x при х≥0; f(x)=0 при х<0.

Искомая функция распределения

F(x)=1-e^-8x при х≥0; F(x)=0 при x<0.

Вероятность попадания в заданный интервал показательно распределенной случайной величины.

Найдем вероятность попадания в интервал (а,b) непрерывной случайной величины ξ, которая распределена по показательному закону, заданному функцией распределения

F(x)=1-e ^{– λx} (х≥0).

Используем формулу

P(a<ξ<b)=F(b)-F(a).

Учитывая, что F(а)=1-e^–λa, F(b)=1-e^–λb, получим

Р(а<ξ<b)=е^-λa–е^-λb.

Значения функции е^-x находят по таблице.

Пример. Непрерывная случайная величина ξ распределена по показательному закону f(x)=2e^-2x при х≥0; f(x)=0 при х<0.

Найти вероятность того, что в результате испытания ξ попадает в интервал (0,3;1).

Решение. По условию, λ=2. Тогда:

Р(0,3<ξ<1)=е^-(2·0,3)-е^-(2·1)=е^-0,6-е^-2=0,54881-0,13534≈0,41.

Нормальное распределение.

Определение. Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

f(x)= e .

Нормальное распределение определяется двумя параметрами: a и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение. Более подробно рассмотрим нормальное распределение дальше.