§7. Условная вероятность, теорема умножения

Пример. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: Ω={4,5,6}, и событию А={выпало четное число очков} благоприятствуют 2 из них: А={4,6}. Поэтому Р(А)=2/3.

П осмотрим на этот вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Ω={1,2,3,4,5,6}. Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие В={4,5,6}. Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении В происходит и А. Вероятность события А, вычисленную в предположении, что нечто о результате эксперимента уже известно (событие В произошло), мы будем обозначать через Р(А|В).

Мы хотим вычислить отношение числа исходов, благоприятствующих А внутри В (то есть благоприятствующих одновременно А и В), к числу исходов, благоприятствующих В.

Р(А|В)= = = .

Определение. Условной вероятностью события А, при условии, что произошло событие В, называется число Р(А|В)=P_B(A)= .

Будем считать, что условная вероятность определена только в случае, когда Р(В)>0. Если Р(В)=0, то соответствующую условную вероятность будем считать также равной нулю.

Следующее свойство называется «теоремой умножения»:

Теорема. Будет верно соотношение Р(А В)=Р(В)Р(А|В)=Р(А)Р(В|А), если соответствующие условные вероятности определены.

Справедливость данной теоремы следует из определения условной вероятности.

Пример. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический.

Решение. Вероятность того, что первый валик окажется конусным (событие А),

Р(А)=3/10.

Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик – конусный, то есть условная вероятность

Р_А(В)=7/9.

По теореме умножения, искомая вероятность

Р(АВ)=Р(А)Р_А(В)=(3/10)(7/9)=7/30.

Заметим, что, сохранив обозначения, легко найдем: Р(В)=7/10, Р_В(А)=3/9, Р(В)Р_В(А)=7/30.

Теорема умножения для большего числа событий:

Теорема. Будет верно соотношение P(A₁ A₂ … A_n)=Р(А₁)Р(А₂|А₁)Р(А₃|А₁ А₂)∙…∙P(A_n|A₁ A₂ … A_n-1), если соответствующие условные вероятности определены.

Доказывается методом математической индукции.

§8. Независимость событий

Определение. События А и В называются независимыми, если

P(A B)=P(A)P(B).

Пример. Найти вероятность совместного появления герба при одном бросании двух монет.

Решение. Вероятность появления герба первой монеты (событие А)

Р(А)=1/2.

Вероятность появления герба второй монеты (событие В)

Р(В)=1/2.

События А и В независимые, поэтому искомая вероятность по теореме умножения равна

Р(АВ)=Р(А)Р(В)=1/2·1/2=1/4.

Пример. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым (событие В) – 0,7.

Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность

Р(АВ)=Р(А)Р(В)=0,7·0,8=0,56.

Пример.

1). Точка с координатами , бросается наудачу в квадрат со стороной 1. Доказать, что для любых x, у R события А={ <x} и В={ <у} независимы.

2). Точка с координатами , бросается наудачу в треугольник с вершинами (1,0), (0,0) и (0,1). Доказать, что события А={ <1/2} и В={ <1/2} зависимы.

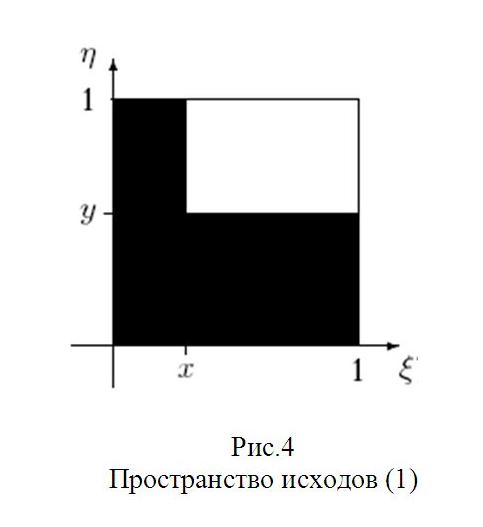
1. Рассмотрим х,у [0;1]. Видим, что Р(А)=х, Р(В)=у, Р(А В)=ху, так что события А={ <х} и В={ <у} независимы.

2. На рисунке событие А заштриховано вертикальными линиями, событие В - горизонтальными. Видим, что Р(А)=3/4, Р(В)=3/4, Р(А В)=1/2≠(3/4)², так что события А={ <1/2} и В={ <1/2} зависимы.

Отметим, что если события А и В несовместны, то они независимы, если и только если Р(А)=0 или Р(В)=0.

Из определения независимости и теоремы умножения следует справедливость следующих утверждений.

Если Р(В)>0, то события А и В независимы тогда и только тогда, когда Р(А|В)=Р(А).

Если Р(А)>0, то события А и В независимы тогда и только тогда, когда Р(В|А)=Р(В).

Лемма. Если события А и В независимы, то независимы и события А и , и В, и .

Доказательство. Так как А=A B А , и события A B и А несовместны, то Р(А)=Р(A B)+P(А ). Поэтому P(А )=Р(А)-Р(A B)= =Р(А)-Р(А)Р(В)=Р(А)(1-Р(В))=Р(А)P( ).

Определение. События А₁,...,А_п называются независимыми в совокупности, если для любого набора 1≤i₁,...,i_k≤n

Р( … )=Р( )·…·Р( ).

Замечание. Если события А₁,...,А_п независимы в совокупности, то они попарно независимы, то есть любые два события A_i,A_j независимы. Достаточно в равенстве определения взять k=2. Обратное, как показывает следующий пример, неверно.

Пример (С.Н. Бернштейна).

Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий, зеленый цвета, а четвертая грань содержит все три цвета. Событие А (В,С) означает, что выпала грань, содержащая красный (синий, зеленый) цвета.

Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность пересечения любых двух из них равна 1/4, так как только одна грань содержит два цвета. А так как 1/4=1/2·1/2, то все события попарно независимы.

Но вероятность пересечения всех трех тоже равна 1/4, а не 1/8, то есть события не являются независимыми в совокупности.

Получили, что равенство определения 3 выполнено для k=2, но не выполнено для k=3.