§31. Характеристические функции

Используем обозначения: i= - мнимая единица, t - вещественная переменная, e^it=cost+isint - формула Эйлера, M(η+iζ)=Mη+iMζ - способ вычисления математического ожидания комплекснозначной случайной величины η+iζ, если математические ожидания ее действительной (η) и мнимой (ζ) частей существуют.

Модулем комплексного числа z=х+iу называется |z|= , так что |e^it|=1.

Определение. Функция φ_ξ(t)=Me^itξ называется характеристической функцией случайной величины ξ.

Пример. Пусть случайная величина ξ имеет распределение Бернулли с параметром р. Ее характеристическая функция равна

φ_ξ(t)=Me^itξ=e^it∙0Р(ξ=0)+e^it∙1Р(ξ=1)=1–р+рe^it.

Пример. Пусть случайная величина ξ имеет биномиальное распределение с параметрами п и р. Ее характеристическая функция равна

φ_ξ(t)=Me^itξ= = = =(1-р+рe^it)ⁿ.

Последнее равенство является биномом Ньютона.

Пример. Пусть случайная величина ξ имеет распределение Пуассона с параметром λ. Ее характеристическая функция равна

φ_ξ(t)=Me^itξ= = =

= = exp{λ(e^it-1)}.

Пример. Пусть случайная величина ξ имеет показательное распределение с параметром α. Ее характеристическая функция равна

φ_ξ(t)=Me^itξ= = = =

= = ,

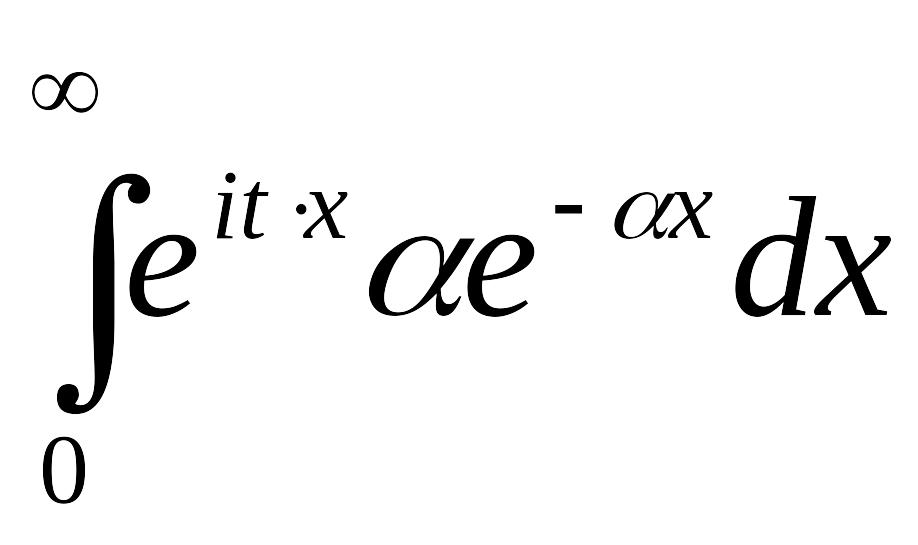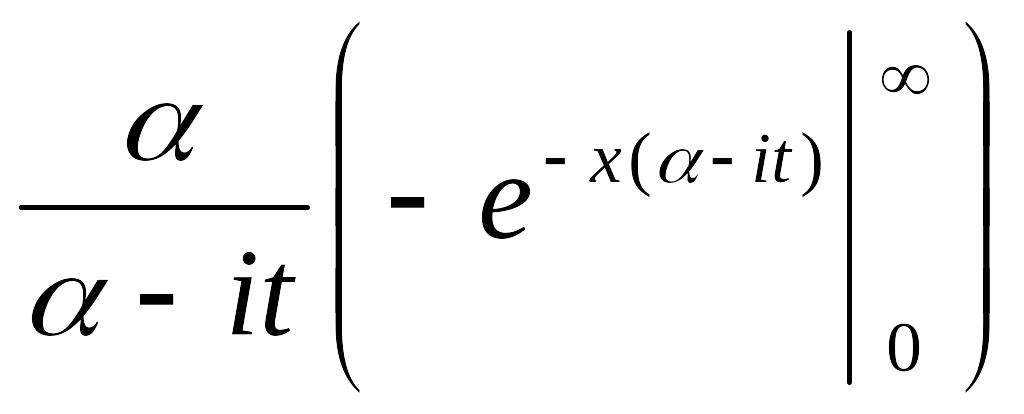поскольку при х→∞ модуль величины е^-х(α-it)=e^-αx·e^itx стремится к нулю: |е^-х(α-it)|=e^-αx→0.

Пример. Пусть случайная величина ξ имеет стандартное нормальное распределение. Ее характеристическая функция равна

φ_ξ(t)= = =

= = .

При интегрировании мы выделили полный квадрат в показателе экспоненты и учли, что интеграл по всей прямой от функции =1.

Свойства характеристических функций.

Свойство 1. Характеристическая функция всегда существует:

|φ_ξ(t)|=|Me^itξ|≤M|e^itξ|=M1=1

Обычные математические ожидания существуют не у всех распределений.

Свойство 2. По характеристической функции однозначно восстанавливается распределение (функция распределения, а также плотность или таблица распределения). То есть если две случайные величины имеют одинаковые характеристические функции, то и распределения этих случайных величин совпадают.

Формулы, с помощью которых это делается, в анализе называют формулами «обратного преобразования Фурье». Например, если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения, и она находится по формуле

f_ξ(x)= .

Ни одна из формул обратного преобразования Фурье нам не понадобится.

Свойство 3. Характеристическая функция случайной величины а+bξ связана с характеристической функцией случайной величины равенством

φ_а+bξ(t)=Me^{it (а+bξ)}=e^itа φ_ξ (tb).

Пример. Вычислим характеристическую функцию случайной величины ξ, имеющей нормальное распределение с параметрами а и σ². У стандартизованной случайной величины ζ= характеристическая функция равна φ_ζ(t)= . Тогда характеристическая функция случайной величины ξ=а+σζ равна

φ_ξ (t)=φ_{а +σζ} (t)=e^itа φ_ζ (tb)=e^itа =exp .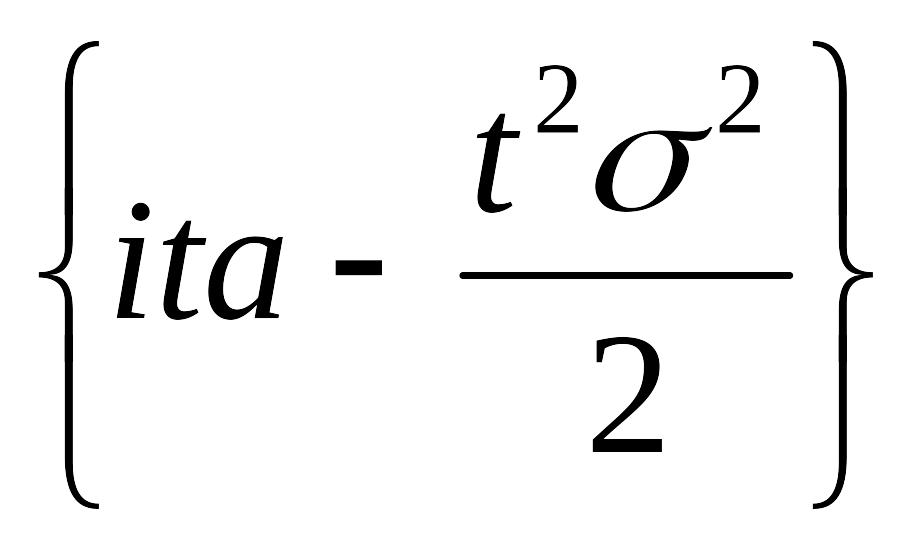

Свойство 4. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: если случайные величины ξ и η независимы, то, по свойству математических ожиданий

φ_ξ+η(t)=Me^it(ξ+η)=Me^itξMe^itη=φ_ξ(t)φ_η(t).

Этим свойством воспользуемся для доказательства леммы, утверждающей устойчивость нормального распределения относительно суммирования.

Лемма. Пусть случайные величины ξ и η независимы. Характеристическая функция суммы ξ+η равна

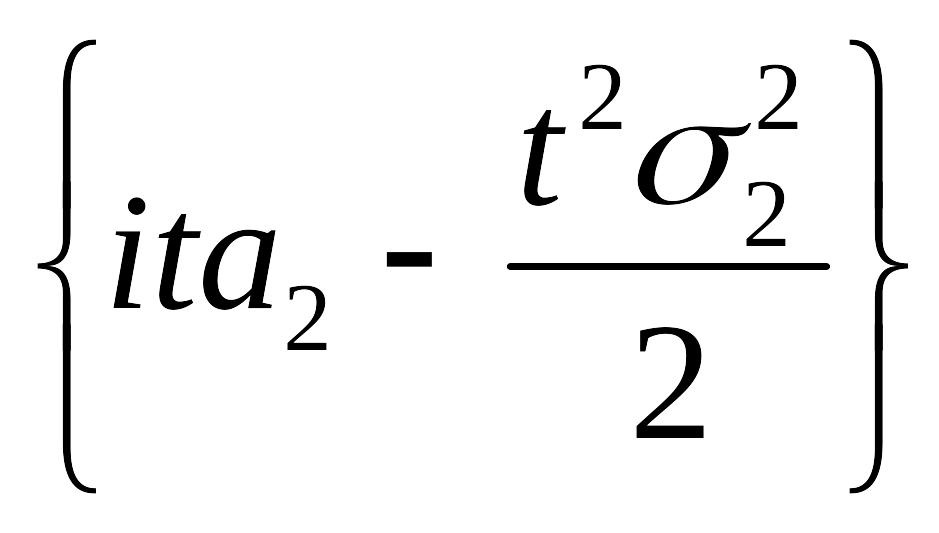φ_ξ+η(t)=φ_ξ(t)φ_η(t)=exp exp =exp .

То есть характеристическая функция суммы есть характеристическая функция нормального распределения с параметрами а₁+а₂, . Тогда ξ+η по свойству характеристической функции.

Пример. Докажем свойства устойчивости по суммированию биномиального распределения и распределения Пуассона, используя вычисленные в предыдущих примерах характеристические функции.

Для независимых случайных величин с распределениями Пуассона П_λ и П_μ характеристическая функция суммы

φ_ξ+η(t)=φ_ξ(t)φ_η(t)=ехр{λ(е^it-1)}ехр{μ(е^it-l)}=ехр{(λ+μ)(е^it-l)}

равна характеристической функции распределения Пуассона с параметром λ+μ.

Для независимых случайных величин с биномиальными распределениями В_п,р и В_т,р характеристическая функция суммы

φ_ξ+η(t)=φ_ξ(t)φ_η(t)=(1-р+рe^it)ⁿ(1-р+рe^it)^т=(1-р+рe^it)^n+т

равна характеристической функции биномиального распределения с параметрами п+m, p.

Свойство 5. Пусть существует момент порядка k=1,2,... случайной величины ξ, то есть M|ξ|^k<∞. Тогда ее характеристическая функция φ_ξ(t) непрерывно дифференцируема k раз, и ее k-я производная в нуле связана с моментом порядка k равенством:

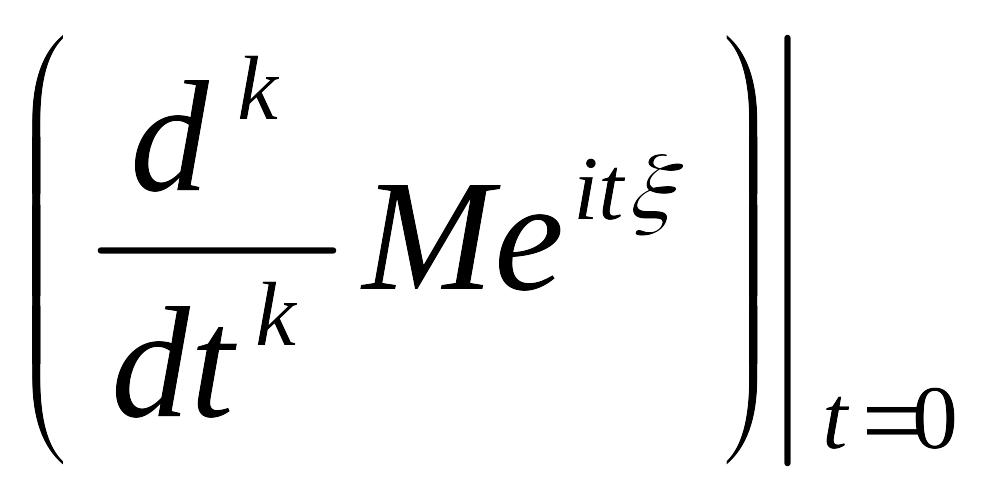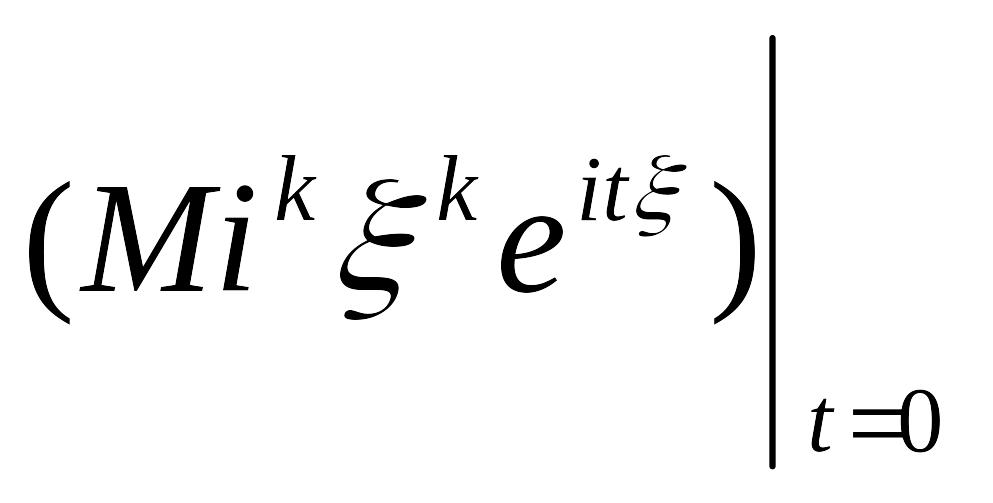= = =i^kMξ^k..

Существование и непрерывность k-й производной, равно как и законность переноса производной под знак математического ожидания мы доказывать не будем.

Свойство 6. Пусть существует момент порядка k=1,2,... случайной величины ξ, то есть M|ξ|^k<∞. Тогда ее характеристическая функция φ_ξ(t) в окрестности точки t=0 разлагается в ряд Тейлора

φ_ξ(t)=φ_ξ(0)+ +o(|t^k|)=1+ +o(|t^k|)=

=1+itMξ- Mξ²+…+ Mξ^k+o(|t^k|).

Ряды Тейлора, как правило, возникают при предельном переходе. Следующее основное свойство характеристических функций потребуется нам для доказательства предельных теорем.

Теорема (о непрерывном соответствии). Случайные величины ξ_п слабо сходятся к случайной величине ξ тогда и только тогда, когда для любого t характеристические функции сходятся к характеристической функции φ_ξ(t).

Слабая сходимость случайных величин имеет место, когда последовательность функций распределений случайных величин ξ_п сходится к функции распределения случайной величины  в точках непрерывности последней.

Сформулированная теорема устанавливает непрерывное соответствие между классами функций распределения со слабой сходимостью и характеристических функций со сходимостью в каждой точке. «Непрерывность» этого соответствия - в том, что пределу в одном классе относительно заданной в этом классе сходимости соответствует предел в другом классе относительно сходимости, заданной в этом классе.