§15. Непрерывные случайные величины

Непрерывную случайную величину можно задать с помощью функции распределения, а также, используя функцию, которую называют плотностью распределения или плотностью вероятности.

Определение Плотностью распределения вероятностей непрерывной случайной величины ξ называют функцию f(х) - первую производную от функции распределения F(х):

f(х)=F´(х).

Из этого определения следует, что функция распределения является первообразной для плотности распределения.

Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

Вероятность попадания непрерывной случайной величины в заданный интервал.

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Вычисление основано на следующей теореме.

Теорема. Вероятность того, что непрерывная случайная величина ξ примет значение, принадлежащее интервалу (а;b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

Р(a<ξ<b)= .

Доказательство. Воспользуемся соотношением Р(a≤ξ<b)=F(b)-F(a).

По формуле Ньютона - Лейбница,

F(b)-F(a)= = .

Таким образом,

Р(a≤ξ<b)= .

Так как Р(a≤ξ<b)=Р(a<ξ<b) то окончательно получим

Р(a<ξ<b)= .

Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а;b), равна площади криволинейной трапеции, ограниченной осью OX, кривой распределения f(х) и прямыми x=a и x=b.

В частности, если f(x) - четная функция и концы интервала симметричны относительно начала координат, то

Р(-а<ξ<а)=Р(|Х|<а)=2 .

Пример. Задана плотность вероятности случайной величины ξ

f(х)=

Найти вероятность того, что в результате испытания ξ примет значение, принадлежащее интервалу (0,5;1).

Решение. Искомая вероятность

Р(0,5<ξ<1)=2 =x²| =1-0,25=0,75.

Нахождение функции распределения по известной плотности распределения.

Зная плотность распределения f(x), можно найти функцию распределения F(х) по формуле

F(x)= .

Действительно, мы обозначили через F(х) вероятность того, что случайная величина примет значение, меньшее х, то есть

F(x)=P(ξ<x).

Очевидно, неравенство ξ<х можно записать в виде двойного неравенства - <ξ<х, следовательно,

F(x)=P(- <ξ<x).

Полагая в формуле Р(a<ξ<b)= а=- , b=х, имеем

Р(- <ξ<х)= .

Наконец, заменив Р(- <ξ<х) на F(x), окончательно получим

F(x)= .

Таким образом, зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения может быть найдена плотность распределения, а именно:

f(х)=F´(х).

Пример. Найти функцию распределения по данной плотности распределения:

f(х)=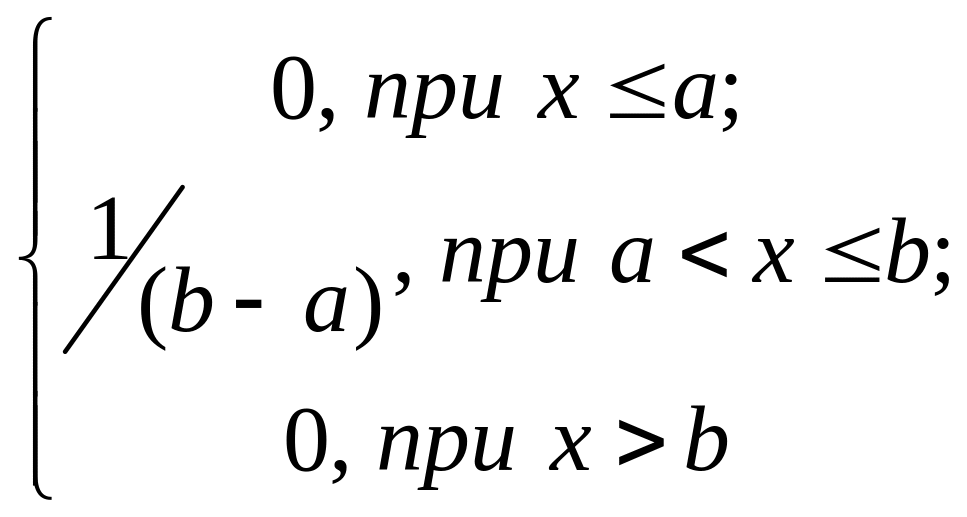

Построить график найденной функции.

Решение. Воспользуемся формулой F(x)= .

Если х≤а, то F(х)=0, следовательно, F(х)=0.

Если а<х≤b, то f(x)=l/(b-а), следовательно,

F(x)= = + = .

Если х>b, то

F(x)= + + = =1.

Итак, искомая функция распределения

F(х)=

Построим график этой функции.

Свойства плотности распределения.

Свойство 1. Плотность распределения - неотрицательная функция:

f(x)≥0.

Доказательство. Функция распределения - неубывающая функция, следовательно, ее производная F’(х)=f(х) - функция неотрицательная.

Геометрически это свойство означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью OX, либо на этой оси.

График плотности распределения называют кривой распределения.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - до равен единице:

=1.

Доказательство. Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу (- , ). Очевидно, такое событие достоверно, следовательно, вероятность его равна единице.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью OX и кривой распределения, равна единице.

В частности, если все возможные значения случайной величины принадлежат интервалу (а,b), то

=1.

Пример. Плотность распределения случайной величины ξ задана:

f(х)= .

Найти постоянный параметр а.

Решение. Плотность распределения должна удовлетворять условию =1, поэтому потребуем, чтобы выполнялось равенство

а =1.

Отсюда

а= .

Найдем неопределенный интеграл:

= =arctg e^x.

Вычислим несобственный интеграл:

= + = (-arctg e^b)+ (arctg e^c)=π/2.

Таким образом, искомый параметр

а= = .

Вероятностный смысл плотности распределения.

Пусть F(x) - функция распределения непрерывной случайной величины ξ. По определению плотности распределения, f(х)=F’(х), или в иной форме

f(х)= .

Разность F(x+∆x)-F(x) определяет вероятность того, что ξ примет значение, принадлежащее интервалу (х,х+∆х). Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу (х,х+∆х) к длине этого интервала (при ∆х→0) равен значению плотности распределения в точке х.

По аналогии с определением плотности массы в точке (если масса непрерывно распределена вдоль оси х по некоторому закону, например F(x), то плотностью ρ(х) массы в точке х называют предел отношения массы интервала (х,х+∆х) к длине интервала при ∆х→0, то есть ρ(х)= ) целесообразно рассматривать значение функции f(х) в точке x, как плотность вероятности в этой точке.

Итак, функция f(х) определяет плотность распределения вероятности для каждой точки х.

Из дифференциального исчисления известно, что приращение функции приближенно равно дифференциалу функции, то есть

F(х,х+∆х)-F(х)≈dF(х),

или

F(х,х+∆х)-F(х)≈F’(x)dx.

Так как F´(x)=f(x) и dx=∆x, то F(х,х+∆х)-F(х)≈f(x) ∆x.

Вероятностный смысл этого равенства таков: вероятность того, что случайная величина примет значение, принадлежащее интервалу (х,х+∆х), приближенно равна (с точностью до бесконечно малых высшего порядка относительно ∆х) произведению плотности вероятности в точке х на длину интервала ∆х.

Геометрически этот результат можно истолковать так: вероятность того, что случайная величина примет значение, принадлежащее интервалу (х,х+∆х), приближенно равна площади прямоугольника с основанием ∆х и высотой f(x).

На рисунке видно, что площадь заштрихованного прямоугольника, равная произведению f(x)∆x, лишь приближенно равна площади криволинейной трапеции (истинной вероятности, определяемой определенным интегралом ). Допущенная при этом погрешность равна площади криволинейного треугольника ABC.