§9. Формула полной вероятности. Формула Байеса

Пример. Есть 3 завода, производящие одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод - 35% и 3-й завод - 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода.

Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1-м заводом, если это изделие бракованное.

Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть 0,05∙0,25+0,03∙0,35+0,04∙0,4. Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть

.

Определение. Набор попарно несовместных событий H₁,H₂,...таких, что P(H_i)>0 для всех i и =Ω, называется полной группой событий или разбиением пространства Ω.

События H₁,H₂,... образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены Р(А|Hi) (вероятность событию А произойти при выполнении «гипотезы» H_i) и собственно Р(H_i) (вероятность выполнения «гипотезы» H_i). Как, используя эти данные, посчитать вероятность события А?

Теорема (Формула полной вероятности). Пусть H₁,H₂,... – полная группа событий. Тогда вероятность любого события А может быть вычислена по формуле:

Р(А)= .

Доказательство. Заметим, что А=А Ω=А = H_i, и события А H_i, А H₂,… попарно несовместны. Поэтому (используем в первом равенстве -аддитивность вероятностной меры, а во втором — теорему умножения)

Р(А)= = .

Теорема (Формула Байеса).

Пусть H₁,H₂,... - полная группа событий и А – некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие Н_k, если в результате эксперимента наблюдалось событие А, может быть вычислена по формуле:

Р(Н_k|А)= .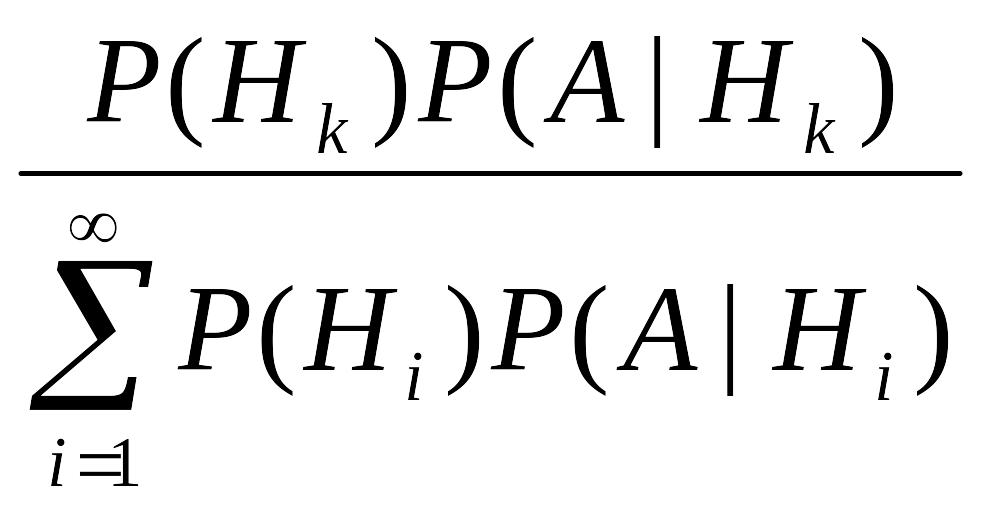

Доказательство. По определению условной вероятности,

Р(Н_k|А)= = .

Последнее равенство следует из теоремы умножения и формулы полной вероятности.

Пример. Вернемся к предыдущему примеру. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: H_i={изделие изготовлено i-м заводом}, i=1,2,3. Вероятности этих событий даны: P(H₁)=0,25, Р(H₂)=0,35, Р(H₃)=0,4. Пусть А={изделие оказалось бракованным}. Даны также условные вероятности Р(А|Н₁)=0,05, Р(А|Н₂)=0,03, Р(А|Н₃)=0,04.

Пример. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок - с вероятностью 0,00001. Можно сделать два предположения об эксперименте: H₁={стреляет 1-й стрелок} и H₂={стреляет 2-й стрелок}. Априорные (a’priori — «до опыта») вероятности этих гипотез одинаковы: Р(Н₁)=Р(H₂)=1/2.

Рассмотрим событие А={пуля попала в мишень}. Известно, что

Р(А|Н₁)=1, Р(А|H₂)=0,00001.

Поэтому вероятность пуле попасть в мишень Р(А)=1/2∙1+1/2∙0.00001. Предположим, что событие А произошло. Какова теперь апостериорная (a’posteriori - «после опыта») вероятность каждой из гипотез H_i? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 100000 раз). Действительно,

Р(А|Н₁)= = ;

Р(А|H₂)= = .