§32. Центральная предельная теорема

Известно, что нормально распределенные случайные величины широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А.М.Ляпуновым (центральная предельная теорема): если случайная величина ξ представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то ξ имеет распределение, близкое к нормальному.

Пример. Пусть производится измерение некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат измерения влияют очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов очень велико, их совокупное действие порождает уже заметную «суммарную ошибку».

Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок, можно заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.

Приведем формулировку центральной предельной теоремы, которая устанавливает условия, при которых сумма большого числа независимых слагаемых имеет распределение, близкое к нормальному.

Пусть ξ₁,ξ₂,...,ξ_п,... - последовательность независимых случайных величин, каждая из которых имеет конечные математическое ожидание и дисперсию: M(ξ_k)=a_k, D(ξ_k)=b .

Введем обозначения:

S_n=ξ₁+ξ₂+...+ξ_n, A_n= , B²= .

Обозначим функцию распределения нормированной суммы через

F_n(x)=P .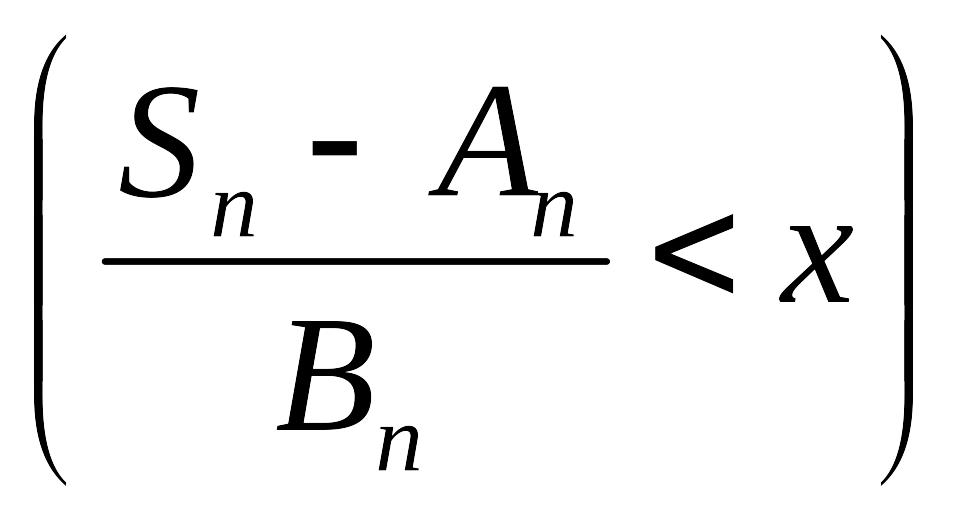

Говорят, что к последовательности ξ₁,ξ₂,... применима центральная предельная теорема, если при любом x функция распределения нормированной суммы при п стремится к нормальной функции распределения:

P = .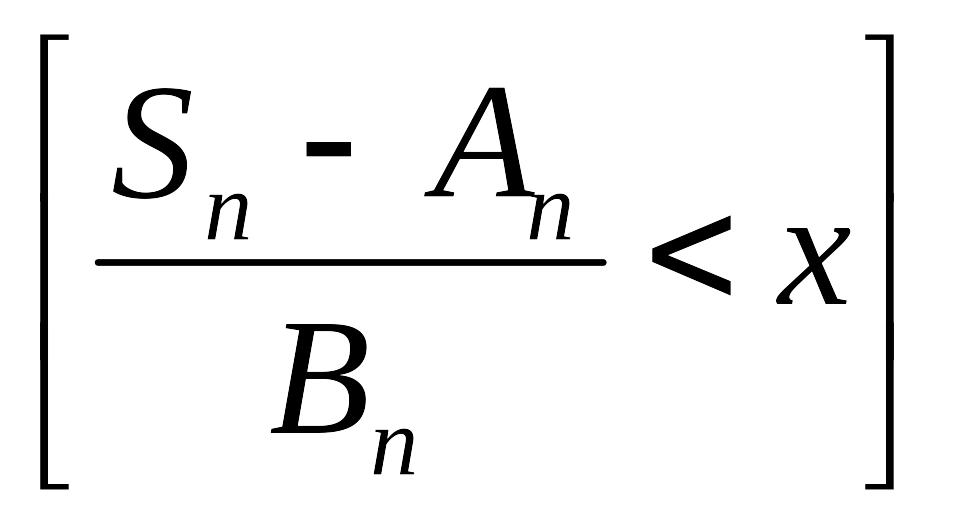

В частности, если все случайные величины ξ₁,ξ₂,... одинаково распределены, то к этой последовательности применима центральная предельная теорема, если дисперсии всех величин ξ_i (i=1,2,...) конечны и отличны от нуля. А.М.Ляпунов доказал, что если для δ>0 при п отношение Ляпунова

L_n=C_n/B , где C_n= |ξ_k–a_k|^2+δ,

стремится к нулю (условие Ляпунова), то к последовательности ξ₁, ξ₂, ... применима центральная предельная теорема.

Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы (S_n-А_п)/В_п оказывало на сумму ничтожное влияние.

Центральная предельная теорема для одинаково распределенных слагаемых.

Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых. Здесь мы сформулируем и докажем одну из самых простых форм центральной предельной теоремы, относящуюся к случаю одинаково распределенных слагаемых.

Теорема. Если ξ₁,ξ₂,...,ξ_п, ...- независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией σ², то при неограниченном увеличении п закон распределения суммы

(1)

неограниченно приближается к нормальному.

Доказательство.

Проведем доказательство для случая непрерывных случайных величин ξ₁,..., ξ_п (для прерывных оно будет аналогичным).

Согласно второму свойству характеристических функций характеристическая функция величины η_n представляет собой произведение характеристических функций слагаемых. Случайные величины ξ₁,...,ξ_п имеют один и тот же закон распределения с плотностью f(х) и, следовательно, одну и ту же характеристическую функцию

φ_ξ(t)= (2)

Следовательно, характеристическая функция случайной величины η_n будет

(t)=[φ_ξ(t)]ⁿ. (3)

Исследуем более подробно функцию φ_ξ(t). Представим ее в окрестности точки t=0 по формуле Маклорена с тремя членами:

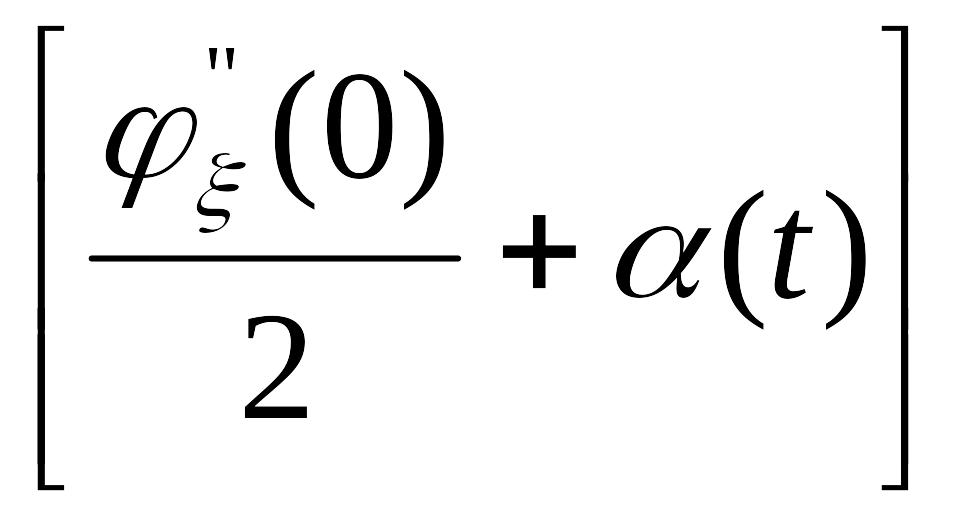φ_ξ(t)=φ_ξ(0)+ (0)t+ t², (4)

где α(t)→0 при t→0.

Найдем величины φ_ξ(0), (0), (0). Полагая в формуле (2) t=0, имеем:

φ_ξ(0)= =1. (5)

Продифференцируем (2) по t:

(0)= =i (6)

Полагая в (6) t=0, получим:

(0)=i =iM[ξ]=im. (7)

Очевидно, не ограничивая общности, можно положить т=0 (для этого достаточно перенести начало отсчета в точку т). Тогда

(0)=0.

Продифференцируем (6) еще раз:

(t)=- ,

отсюда

(0)=- . (8)

При m=0 интеграл в выражении (8) есть не что иное, как дисперсия величины ξ с плотностью f(х), следовательно

(0)=-σ² (9)

Подставляя в (4) φ_ξ(0)=1, (0)=0, (0)=-σ², получим:

φ_ξ(t)=1-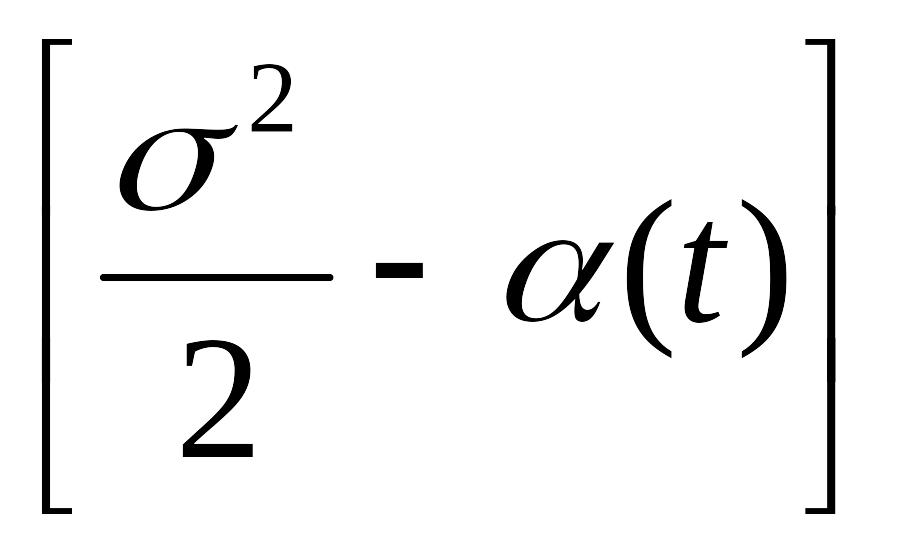 t². (10)

Обратимся к случайной величине η_n. Мы хотим доказать, что ее закон распределения при увеличении п приближается к нормальному. Для этого перейдем от величины η_n к другой («нормированной») случайной величине

θ_п= (11)

Эта величина удобна тем, что ее дисперсия не зависит от п и равна единице при любом п. В этом нетрудно убедиться, рассматривая величину θ_п как линейную функцию независимых случайных величин ξ₁,ξ₂,...,ξ_п, каждая из которых имеет дисперсию σ². Если мы докажем, что закон распределения величины θ_n приближается к нормальному, то, очевидно, это будет справедливо и для величины η_п, связанной с θ_n линейной зависимостью (11).

Вместо того чтобы доказывать, что закон распределения величины θ_n при увеличении п приближается к нормальному, покажем, что ее характеристическая функция приближается к характеристической функции нормального закона.

Найдем характеристическую функцию величины θ_n. Из соотношения (11), согласно первому свойству характеристических функций, получим

, (12)

где характеристическая функция случайной величины η_п.

Из формул (12) и (3) получим

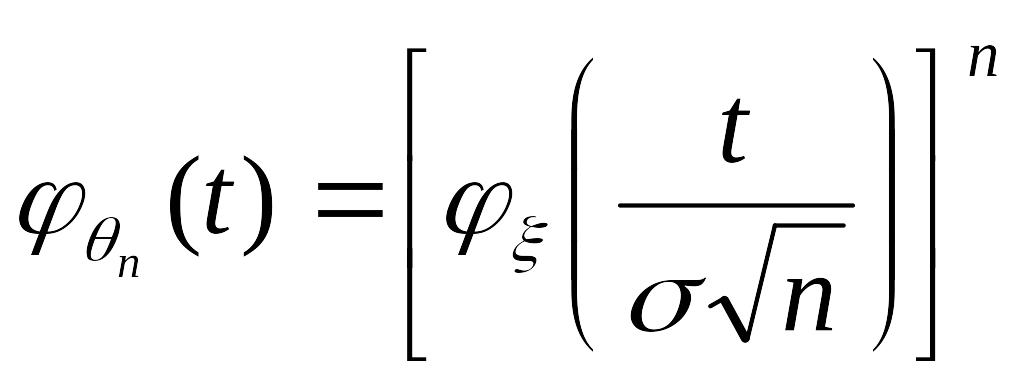(13)

или, пользуясь формулой (10),

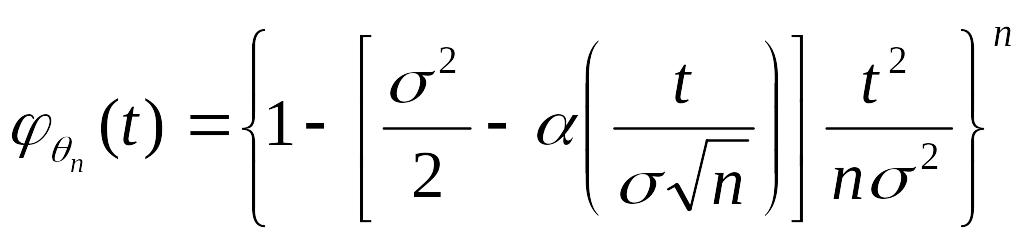. (14)

Прологарифмируем выражение (14):

ln .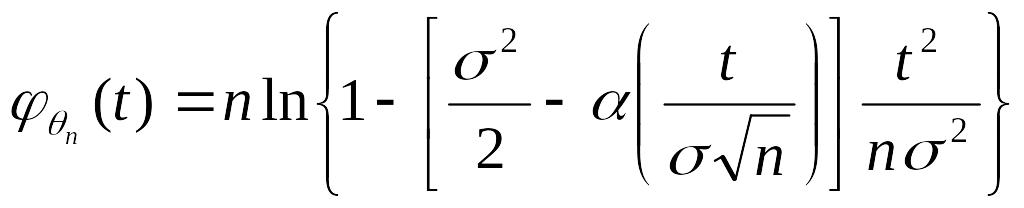

Введем обозначение

=x. (15)

Тогда

ln

Будем неограниченно увеличивать п. При этом величина x, согласно формуле (15), стремится к нулю. При значительном п ее можно считать весьма малой. Разложим ln{1-х} в ряд и ограничимся одним членом разложения (остальные при n→∞ станут пренебрежимо малыми):

ln{1-х}≈-х.

Тогда получим

(t)= n(-x)= =- + .

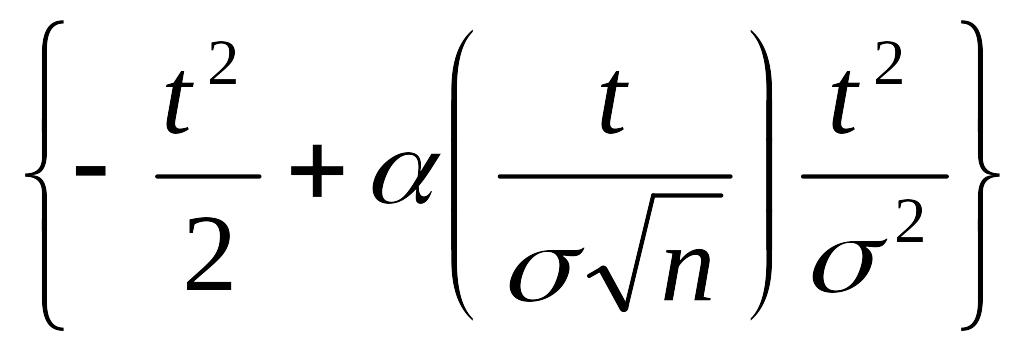По определению функция α(t) стремится к нулю при t→0; следовательно,

=0

и

(t)=- ,

откуда

(t)= . (16)

Это есть не что иное, как характеристическая функция нормального закона с параметрами т=0, σ=1.

Таким образом, доказано, что при увеличении п характеристическая функция случайной величины θ_n неограниченно приближается к характеристической функции нормального закона; отсюда заключаем, что и закон распределения величины θ_n (а значит и величины η_п) неограниченно приближается к нормальному закону. Теорема доказана.

Мы доказали центральную предельную теорему для частного, но важного случая одинаково распределенных слагаемых. Однако в достаточно широком классе условий она справедлива и для неодинаково распределенных слагаемых. Например, А.М.Ляпунов доказал центральную предельную теорему для следующих условий:

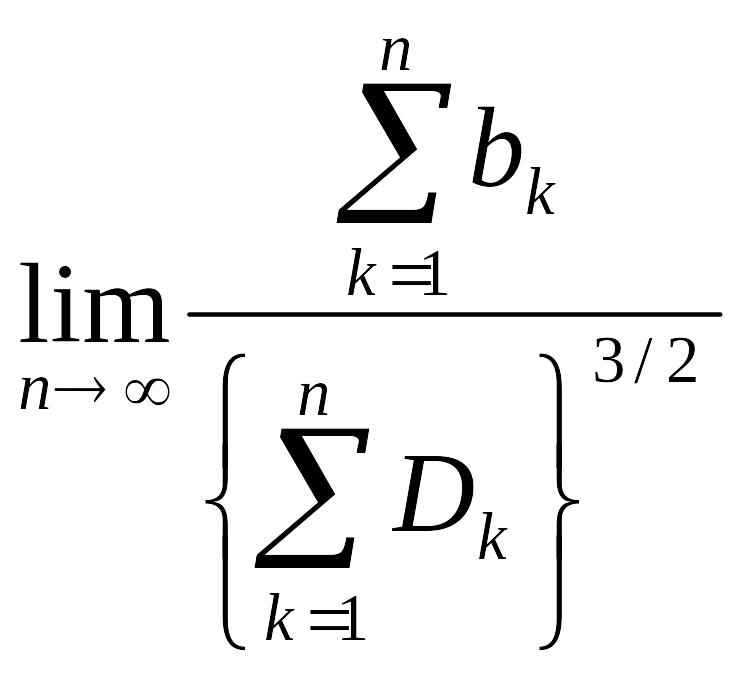=0,

где b_k - третий абсолютный центральный момент величины ξ_k: b_k=ν₃[ξ_k]=M[| |³] (k=1,…,n), D_k - дисперсия величины ξ_k.

Наиболее общим (необходимым и достаточным) условием справедливости центральной предельной теоремы является условие Линдеберга: при любом τ>0

=0,

где m_k - математическое ожидание, f_k(х) - плотность распределения случайной величины ξ_k, B_n= .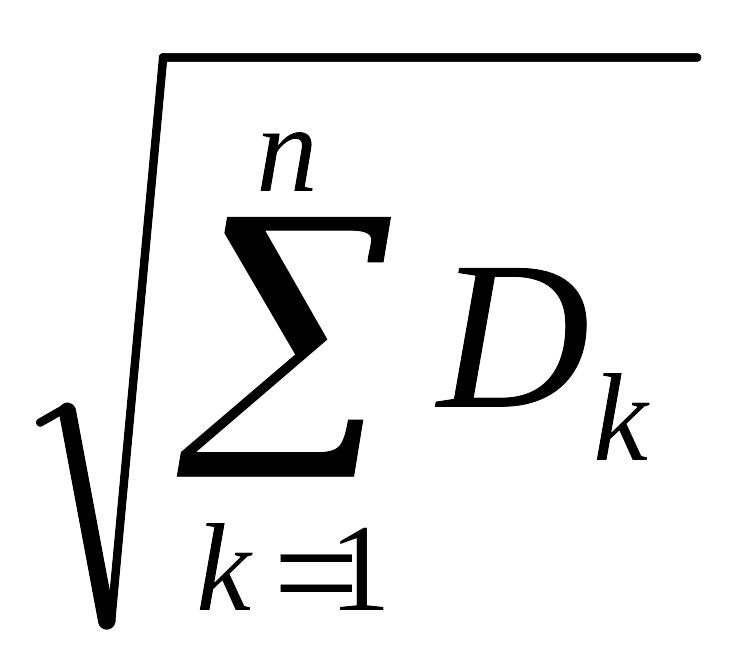

Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении.

Согласно центральной предельной теореме, закон распределения суммы достаточно большого числа независимых случайных величин (при соблюдении некоторых нежестких ограничений) сколь угодно близок к нормальному.

Практически центральной предельной теоремой можно пользоваться и тогда, когда речь идет о сумме сравнительно небольшого числа случайных величин. При суммировании независимых случайных величин, сравнимых по своему рассеиванию, с увеличением числа слагаемых закон распределения суммы очень скоро становится приблизительно нормальным. На практике вообще широко применяется приближенная замена одних законов распределения другими; при той сравнительно малой точности, которая требуется от вероятностных расчетов, такая замена тоже может быть сделана крайне приближенно. Опыт показывает, что когда число слагаемых порядка десяти (а часто и меньше), закон распределения суммы обычно может быть заменен нормальным.

В практических задачах часто применяют центральную предельную теорему для вычисления вероятности того, что сумма нескольких случайных величин окажется в заданных пределах.

Пусть ξ₁,ξ₂,...,ξ_п - независимые случайные величины с математическими ожиданиями

т₁,т₂,...,т_п

и дисперсиями

D₁,D₂,...,D_п.

Предположим что условия центральной предельной теоремы выполнены (величины ξ₁,ξ₂,...,ξ_п сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых п достаточно для того, чтобы закон распределения величины

η=

можно было считать приближенно нормальным.

Тогда вероятность того, что случайная величина η попадает в пределы участка (α,β), выражается формулой

P(α<η<β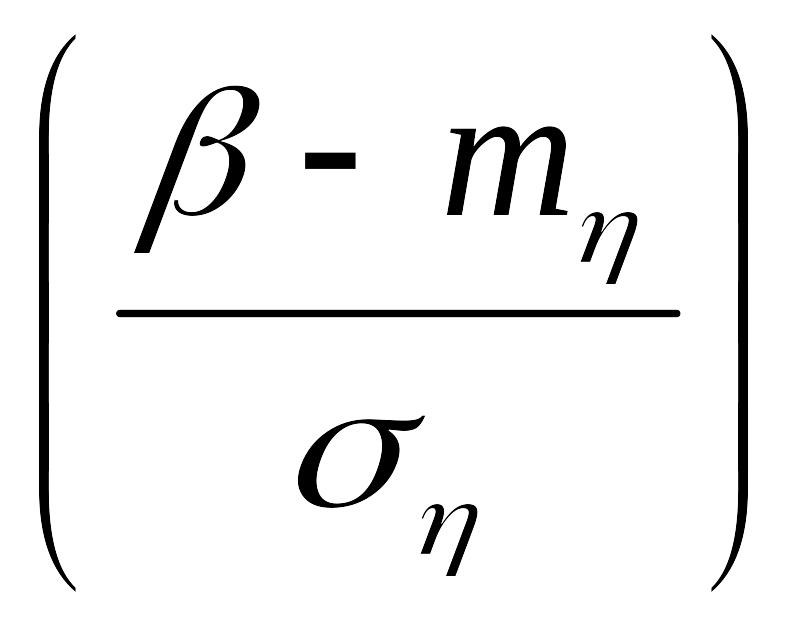)=Ф -Ф ,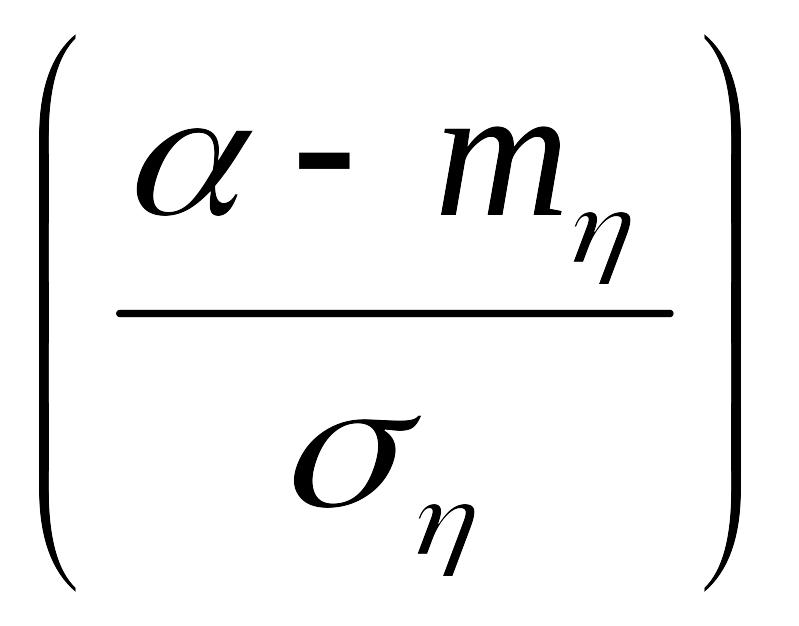

где т_η, σ_η - математическое ожидание и среднее квадратическое отклонение величины η, Ф - нормальная функция распределения. Согласно теоремам сложения математических ожиданий и дисперсий

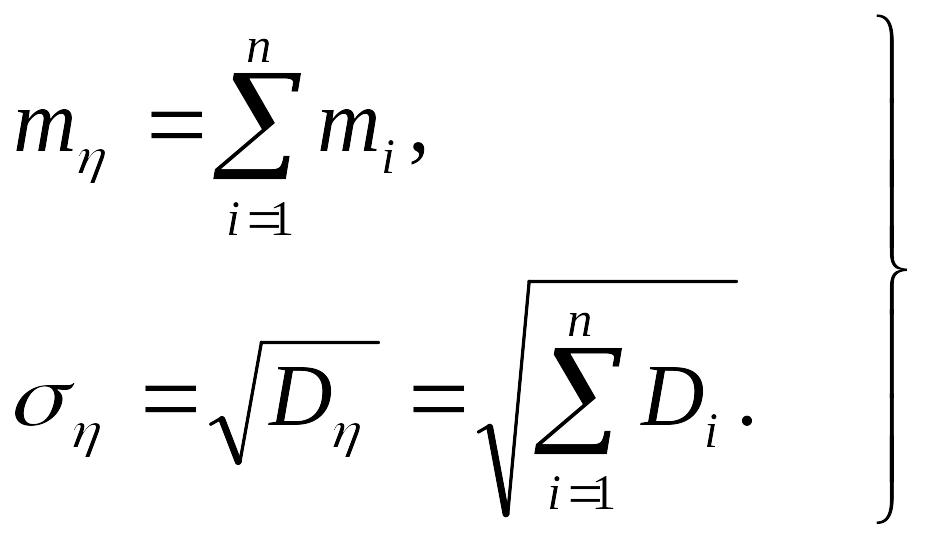
Таким образом, для того чтобы приближенно найти вероятность попадания суммы большого числа случайных величин на заданный участок, не требуется знать законы распределения этих величин; достаточно знать лишь их характеристики. Разумеется, это относится только к случаю, когда выполнено основное условие центральной предельной теоремы - равномерно малое влияние слагаемых на рассеивание суммы.

На практике часто применяются формулы, в которых вместо суммы случайных величин ξ_i фигурирует их нормированная сумма

θ= = .

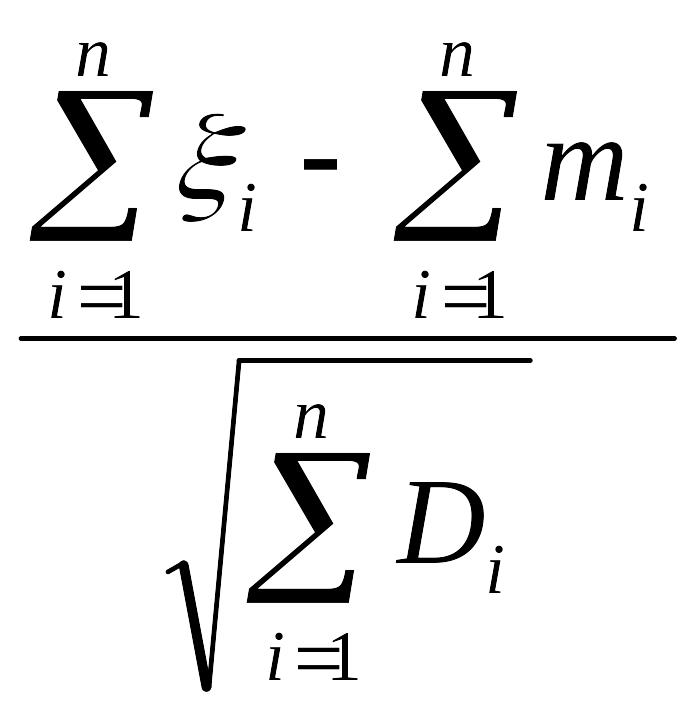Очевидно,

M[θ]=0; D[θ]=σ_θ=1.

И в этом случае закон распределения величины θ близок к нормальному с параметрами m_θ=0, σ_θ=1. Отсюда

P(α<θ<β)=Ф(β)-Ф(α).

Заметим, что центральная предельная теорема может применяться не только к непрерывным, но и к дискретным случайным величинам при условии, что мы будем оперировать не плотностями, а функциями распределения. Действительно, если величины ξ₁,ξ₂,...,ξ_п дискретны, то их сумма ξ - также дискретная случайная величина и поэтому, строго говоря, не может подчиняться нормальному закону. Однако все соотношения остаются в силе, так как в них фигурируют не плотности, а функции распределения. Можно доказать, что если дискретные случайные величины удовлетворяют условиям центральной предельной теоремы, то функция распределения их нормированной суммы θ при увеличении п неограниченно приближается к нормальной функции распределения с параметрами m_θ=0, σ_θ=1.

Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема Лапласа.

Теорема. Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение

P(α< <β)=Ф(β)-Ф(α).

где η - число появлений события А в п опытах, q=1-р.

Доказательство. Пусть производится п независимых опытов, в каждом из которых с вероятностью р может появиться событие А. Представим случайную величину η - общее число появлений события в п опытах - в виде суммы

η=

где ξ_i - число появлений события А в i-м опыте.

Согласно центральной предельной теореме, закон распределения суммы одинаково распределенных слагаемых при увеличении их числа приближается к нормальному закону. Следовательно, при достаточно большом п справедлива формула

P(α<θ<β)=Ф(β)-Ф(α),

где θ= .

Математическое ожидание и дисперсия числа появлений события в п независимых опытах равны:

т_η=пр, D_η=npq (q=1-р).

С учетом этого получим

θ= ,

и окончательно можно записать:

P(α< <β)=Ф(β)-Ф(α).

Теорема доказана.