2.5. Установление существенности связи на основе теории статистической проверки гипотез

Прежде чем перейти к статистической проверке гипотез, напомним некоторые сведения из теории вероятностей о необходимых для дальнейшего анализа распределениях случайных величин.

2.5.1. Распределения случайных величин Нормальное распределение (Гаусса)

Случайная величина Х называется нормальной, если её плотность вероятности описывается законом Гаусса

, (2.43)

где m_x = M[X] – математическое ожидание,

_x² =D[X] – дисперсия случайной величины Х.

Таким образом, распределение нормальной случайной величины (НСВ) полностью определяется двумя параметрами – средним значением и дисперсией. Для НСВ принято обозначение: Х  N(m_x,_x²). Нормальная случайная величина называется стандартной, если она имеет нулевое среднее и единичную дисперсию: Z  N(0,1). Любая нормальная случайная величина может быть приведена к стандартной преобразованием

,

так как Плотность вероятности стандартной НСВ имеет вид

.

Распределение (2.43) при показано на рис.2.11.

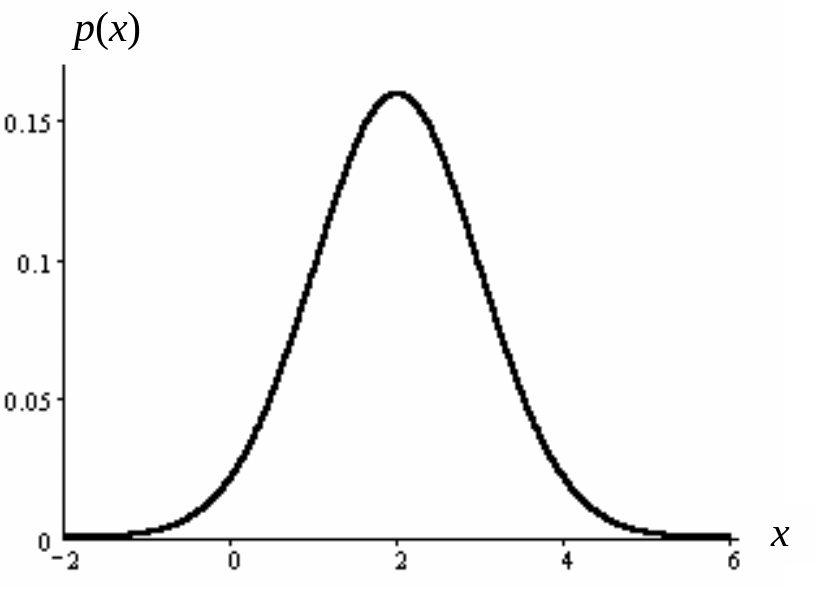
Рис.2.11

Некоторые важные свойства нормальной случайной величины:

• сумма (разность) двух и более нормальных случайных величин является нормальной случайной величиной;

• линейные преобразования нормальной случайной величины дают нормальную случайную величину.

Отсюда, в частности, следует, что если МЛР является нормальной (ошибки моделирования _i – НСВ), то оценки её параметров – тоже нормальные случайные величины. Например, из (2.27) следует, что

и при этом оценка коэффициента регрессии является линейной комбинацией (взвешенной суммой) нормальных случайных величин у_i, и, следовательно, является нормальной случайной величиной. Аналогично можно показать, что оценка параметра а модели также является НСВ.

Распределение Пирсона (2-распределение)

Пусть {₁, ₂, ₃,…, _n} – независимые стандартные нормальные случайные величины (_i  N(0, 1)). Тогда сумма их квадратов образует случайную величину

, (2.44)

имеющую ²-распределение (хи-квадрат) с n степенями свободы

р(х) = 2^–n/2Г^-1(n/2) x ^{n/2 – 1}exp{– x/2}, x > 0, (2.45)

В частности, для целых чисел Г(n) = (n – 1)!. Распределение (2.45) показано на рис. 2.12. Оно имеет одинаковые значения математического ожидания и дисперсии .

Рис.2.12

С ростом n это распределение сдвигается вправо. При достаточно больших значениях n оно приближается к нормальному распределению. На графике рис.2.12 кривая слева соответствует значению n = 4, а справа – значению n = 10.

Распределение Фишера

Пусть две совокупности {₁, ₂, ₃,…, _m} и {₁, ₂, ₃,…, _n} – независимые стандартные нормальные случайные величины (_i  N(0, 1), _i  N(0, 1)). Тогда случайная величина

(2.46)

имеет распределение Фишера (рис.2.13) с (m, n) степенями свободы

Здесь Г(q) – гамма-функция. Параметр m называют степенью свободы числителя случайной величины (2.46), а n – степенью свободы знаменателя.

Рис.2.13

Математическое ожидание этого распределения при n > 4

M[F(m, n)] = n/(n – 2) > 1.

С ростом n это распределение сдвигается влево, но при больших n > 20 практически не меняется.

Распределение Стьюдента (t-распределение)

Пусть {₀, ₁, ₂,…, _n} – независимые стандартные нормальные СВ (_i  N(0, 1)). Тогда распределение случайной величины

(2.47)

называется распределением Стьюдента или t-распределением с n степенями свободы. Так как распределение независимых случайных величин определяется произведением их одномерных распределений, то в силу нормальности величины ₀ с нулевым средним распределение величины t также описывается четной функцией

, –  < t < .

Оно имеет вид (рис.2.14), подобный стандартному нормальному распределению (т.е. симметрично относительно сечения t = 0). Его математическое ожидание и дисперсия при n > 2 соответственно равны:

М[t] = 0, D[t] = n/(n – 2).

При n = 1 распределение Стьюдента называется распределением Коши.

Рис.2.14

F-статистика для двухмерной МЛР

Будем полагать, что модель линейной регрессии является нормальной, т.е. её ошибки имеют нормальное распределение с нулевым средним и дисперсией ². Линейное уравнение модели

имеет параметры a, b, являющиеся нормальными случайными величинами с дисперсиями

и оценкой дисперсии ошибок регрессии

.

Статистическая связь показателя у и фактора х определяется коэффициентом регрессии b и не зависит от a. Приведем оценки b и s² к стандартным распределениям. Так как оценка b несмещенная (М[b] = ), то

. (2.48)

Оценку дисперсии ошибок нормируем к её математическому ожиданию М[e_i²]=  ², тогда нормированная случайная величина выражается как

(2.49)

Сформируем F-статистику (2.46) как отношение

(2.50)

С учетом (2.36), (2.48), (2.49) её можно выразить через выборочные данные

. (2.51)

Эта величина используется при статистической проверке гипотезы о существенности (значимости) связи между Х и Y.