2.2. Матричная форма записи при определении параметров млр

Сначала дадим векторную интерпретацию при решении системы уравнений для параметров a и b , полученных с помощью МНК. Введем обозначения для n-мерных вектор-строк:

X₁ = (1, 1, 1,……, 1),

Х₂ = (х₁, х₂, х₃,…, х_n),

E = (e₁, e₂, e₃,…, e_n).

Обозначая штрихом Х транспонирование строки (или матрицы) Х (при котором строки преобразуются в столбцы и наоборот), система уравнений (2.4), (2.5) в векторной форме примет вид

, (2.13)

. (2.14)

Равенство нулю векторного произведения двух векторов определяется как свойство ортогональности этих векторов. Отсюда следует, что вектор остатков регрессии Е минимальной длины ( ) ортогонален векторам Х₁ (с единичными проекциями) и Х₂ (с проекциями х_i). Включая строки Х₁ и Х₂ в матрицу Х размерности 2  n

,

систему уравнений (2.13), (2.14) можно заменить одним матричным уравнением

. (2.15)

Здесь 0 – двухмерный вектор-строка с нулевыми проекциями. Вектор остатков регрессии теперь запишем в виде

, (2.16)

где Y = (y₁, y₂, y₃,…, y_n),

Y^* = (a + bx₁, a + bx₂, a + bx₃,…, a + bx_n ) = ВХ,

В = (a, b).

Вектор В является двухмерным вектором оценок параметров двухмерной МЛР.

С учетом (2.16) и последних соотношений уравнение (2.15) примет вид

.

Отсюда решение для вектора В оценок параметров модели имеет вид

. (2.17)

Здесь []^–1 обозначена обратная матрица. Можно показать, что это решение тождественно решениям (2.9), (2.10) системы двух уравнений для оценок параметров двухмерной МЛР. Отметим, что в (2.17) В и – векторы-строки размерности 2, а – квадратная матрица размерности [22].

Решение (2.17) существует, если матрица невырождена, т.е. её определитель не равен 0 (условие существования обратной матрицы). Так как

,

то определитель этой матрицы равен 0 тогда и только тогда, когда все элементы выборки – одинаковые константы: x_i = c. Это вырожденный случай, так как область значений фактора вырождается в точку и регрессия отсутствует. Выборочная дисперсия (2.10) фактора в этом случае равна 0, и в формуле (2.12) появляется неопределенность 0/0 (К_ху = 0, так как ). В практических задачах моделирования регрессий или трендов такие ситуации нереальны или не представляют интереса.

Матричная форма записи (2.17) для вектора В оценок параметров линейной модели парной регрессии полезна при обобщении двухмерной модели в модель множественной регрессии (см. главу 3, формула (3.9)).

2.3. Корреляционный анализ млр

Корреляционный анализ имеет целью установление существенности (статистической значимости) корреляционной связи между фактором и результатом (показателем). Основным и достаточно удобным параметром для этого является коэффициент детерминации.

Пользуясь обозначениями п.2.1, разложим выборочную дисперсию показателя на две некоррелированные составляющие:

.

Из (2.4), (2.5) следует, что последняя сумма в этом разложении равна 0, и, следовательно, случайные величины e_i и некоррелированы. Поэтому

, (2.18)

где , (2.19)

. (2.20)

Таким образом, общая дисперсия (2.18) показателя (TSS – total sum of squares – общая сумма квадратов) складывается из двух составляющих, характеризующих разные свойства корреляционного поля данных. Составляющая (2.20) (ESS – error sum of squares – сумма квадратов ошибок) характеризует степень разброса точек у_i относительно теоретической прямой и, следовательно, выражает свойство случайности выборочной совокупности. Составляющая (2.19) (RSS – regression sum of squares – сумма квадратов отклонений регрессии), напротив, пропорциональна квадрату разности между линией регрессии и постоянной средней, т.е. характеризует свойство закономерности связи. её доля в общей дисперсии, определяемая как коэффициент детерминации

, (2.21)

является параметром, определяющим значимость линейной статистической связи между фактором и показателем. Из (2.18) – (2.20) следует, что

. (2.22)

Эта формула удобна при расчетах, если по результатам моделирования вычислены остатки регрессии e_i и их квадраты.

Коэффициент детерминации можно также выразить через коэффициент регрессии b, если учесть, что возведение в квадрат (2.7) и усреднение дает

.

Тогда

, (2.23)

или, учитывая (2.12),

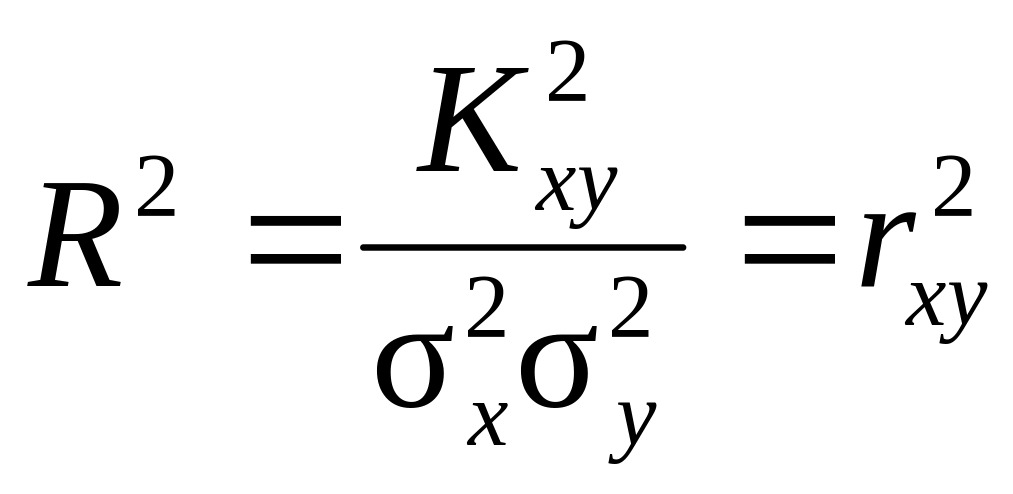. (2.24)

Таким образом, коэффициент детерминации равен квадрату коэффициента корреляции

. (2.25)

Согласно (2.23) коэффициент корреляции можно выразить через коэффициент регрессии как

.

Таким образом, знак коэффициента корреляции совпадает со знаком коэффициента регрессии b. Последний, однако, отличается тем, что может иметь размерность [y/x], тогда как коэффициент корреляции r_xy – величина безразмерная.

Коэффициент корреляции характеризует степень линейной статистической связи. Он принимает значения в интервале

– 1  r_xy  1. (2.26)

В крайних точках r_xy =  1 статистическая связь становится линейной функциональной, положительной (r_xy = 1) или отрицательной (r_xy = – 1). В области r_xy (0, 1] регрессия положительна (b  0), а в области r_xy  [– 1, 0) – отрицательна (b  0). При r_xy = 0 говорят, что величины X и Y некоррелированы. В теории вероятности доказано, что независимые случайные величины всегда некоррелированы (обратное утверждение верно лишь в частных случаях, например, для нормальных случайных величин X и Y). Обычно полагают, что при |r_xy| < 0,3 корреляционная связь слабая, при |r_xy| = (0,30,7) – средняя, а при |r_xy| > 0,7 – сильная.

Коэффициент корреляции является более информативным параметром по сравнению с коэффициентом детерминации, так как его знак позволяет судить о положительной или отрицательной корреляции (и, тем самым, регрессии). В соответствии с (2.22) или (2.26) область значений коэффициента детерминации

0  R²  1.

Важным свойством коэффициентов корреляции и детерминации является их независимость от изменения размерности величин Х и (или) Y, а также от их пропорционального изменения. Скажем, мы изучаем зависимость товарооборота Y торгового предприятия от торговой площади X [м²]. Коэффициент регрессии b при этом измеряется в ден.ед./м², например, грн./м² или евро/м². Переход от одной единицы к другой сопровождается пропорциональным изменением коэффициента регрессии b (а также и постоянной составляющей а, если изменяется показатель Y). Вместе с тем, на коэффициенты R² и r_xy такие пересчеты не влияют, они являются безразмерными относительными показателями (коэффициент R² можно, например, выразить в %). Как следует из формул (2.24), (2.25), изменение всех значений x_i в k₁ раз и (или) y_i в k₂ раза оставляет неизменными коэффициенты корреляции и детерминации.

Коэффициент детерминации (или связанный с ним F-критерий Фишера) является определяющим показателем при установлении существенности (статистической значимости) связи между фактором и показателем (см.п.2.5).