2.4.3. Оптимальность оценок мнк Теорема Гаусса-Маркова.

П ри выполнении гипотез 1 – 4 параграфа 2.4.1 оценки а, b параметров МЛР, полученные методом наименьших квадратов, имеют минимальную дисперсию в классе линейных несмещенных оценок.

Д окажем эту теорему для дисперсии оценки коэффициента регрессии

.

Пусть

(2.38)

любая другая несмещенная оценка коэффициента регрессии. Положим

. (2.39)

Тогда из условия несмещенности оценок

следует, что

. (2.40)

Следовательно, дисперсия оценки (2.38) с учетом (2.39), (2.40) равна

.

Таким образом, любая другая несмещенная оценка параметра b дает дисперсию не меньшую, чем дисперсия оценки МНК. Это доказывает утверждение теоремы и оптимальность оценок МНК в классе линейных оценок.

2.4.4. Оценка прогноза показателя и ошибок прогнозирования

Всегда следует помнить, что одной из основных задач моделирования является в конечном итоге получить результат прогноза показателя Y для какого-то интересующего экономиста значения фактора х_р (в точке прогноза). Скажем, при построении модели семейных расходов на питание в зависимости от числа членов семьи в выборку вошли семьи до 5 человек, а мы хотим спрогнозировать эти расходы для семьи из 7 человек (х_р = 7). Среднее значение прогноза показателя в точке прогноза х_р легко определяется из уравнения модели

.

После нахождения среднего значения прогноза всегда возникает традиционный вопрос: какова точность прогноза, какова степень его надежности. Обычно для этого привлекаются интервальные оценки ошибок моделирования (доверительный интервал вместе с доверительной вероятностью). Для каждого значения прогноза ошибки оказываются различными. Это естественно, если вспомнить, что ошибки, например, в прогнозе погоды, растут с увеличением времени до точки прогноза (прогноз на завтра более точен, чем на неделю вперед).

Определим дисперсию и среднеквадратичную ошибку прогноза показателя у_р. В спецификации модели (2.28) для отклонений заменим точку наблюдения x_i на прогнозную точку x_p:

.

Входящие в последнее выражение случайные величины некоррелированны, поэтому дисперсия показателя складывается из дисперсий слагаемых и равна

.

Здесь были использованы выражения для дисперсий среднего значения показателя и коэффициента регрессии, полученные в п.2.4.2. Как и ранее, вместо точного значения дисперсии ошибок ² (которое неизвестно в рамках выборочного наблюдения) следует подставить её оценку (2.35), тогда СКО прогноза показателя становится равной

. (2.41)

Эта среднеквадратичная ошибка, как и следовало ожидать, пропорциональна СКО остатков регрессии s и растет с увеличением разности между прогнозным и средним значениями фактора . Граничная ошибка для определения доверительного интервала равна

, (2.42)

а границы доверительного интервала прогнозируемого показателя расширяются пропорционально

коэффициенту доверия t. Напомним, что для нормальной модели значение t = 1 соответствует доверительной вероятности Р = 0,68, t = 2 – доверительной вероятности Р = 0,954 и t = 3 – доверительной вероятности Р = 0,997.

Очевидно, с удалением точки прогнозного фактора х_р от среднего зона доверительного интервала расширяется (рис.2.6). Это отвечает интуитивному восприятию ошибок прогноза, обычно возрастающих при удалении от средних показателей. Максимальная точность прогноза, как это следует из (2.41), достигается в точке .

Рис.2.6

Пример 2.3. Пусть известны данные для 10 торговых предприятий по товарообороту Y (тыс. грн) и величине торговой площади Х (м²), которые приведены в первых двух колонках таблицы 2.4. Требуется построить модель линейной регрессии на фоне выборочных точек (диаграммы рассеяния), а также определить среднее значение прогноза товарооборота при торговой площади х_р = 1150м² и доверительный интервал этого прогноза с вероятностью 0,68.

Расчеты, необходимые для определения параметров модели, среднего значения прогноза и СКО прогноза, сведем в таблицу 2.2. Они легко выполняются с помощью электронных таблиц EXCEL. В верхней ячейке каждой колонки создается формула расчета, после чего нажатием левой кнопки мыши на крестике в правом нижнем углу ячейки эта формула протаскивается по всем 10 ячейкам каждого столбца. В последней строке таблицы рассчитаны суммы чисел каждого столбца. Убеждаемся, что суммы отклонений показателя, фактора и сумма остатков регрессии равны 0.

Согласно (2.12), (2.9) определяем оценки параметров модели:

Уравнение модели, следовательно, имеет вид

y^* = – 60,4723 + 0,1744x.

Таблица 2.2

i	yi, тыс. грн.	xi, м2						y*(xi)	ei	ei2
1	124	1090	24	170	4080	28900	576	129,652	5,65249	31,9506
2	110	995	10	75	750	5625	100	113,082	3,08198	9,49860
3	114	1020	24	100	2400	10000	576	117,443	-6,5574	42,9990
4	112	960	12	30	360	900	144	105,233	-6,7672	45,7951
5	98	880	-2	-40	80	1600	4	93,0229	-4,9771	24,7711
6	105	940	5	20	100	400	25	103,488	-1,5115	2,28455
7	86	850	-14	-70	980	4900	196	87,7902	1,79015	3,20464
8	102	900	-8	-20	160	400	64	96,5115	4,51147	20,3534
9	73	815	-27	-105	2835	11025	729	81,6852	8,68523	75,4332
10	76	770	-24	-160	3840	25600	576	72,0918	-3,9082	15,2742
	1000	9220	0	0	15585	89350	2990	999,9996	0	271,5644

График поля выборочных точек вместе с прямой y^*(х) представлен на рис.2.7. Прямая линия МЛР проходит через точку средних значений ( = 920, = 100). Этот график (как и график на рис.2.1) можно получить в EXCEL с помощью функций «ДИАГРАММА – Точечная – Добавить линию тренда – Линейная». После активизации точечной диаграммы в меню «ДИАГРАММА» выбирается команда «Добавить линию тренда» и появляется окно, рис.2.8. С помощью вкладки «Параметры» (для аппроксимирующих функций, общее число которых равно 6) можно вывести в области графика уравнение функции (в нашем примере – прямой линии) и значение коэффициента детерминации R².

Среди встроенных функций EXCEL для регрессионного анализа особый интерес представляют функции «ЛИНЕЙН» (LINEAR) и «ТЕНДЕНЦИЯ» (TREND). Первая предназначена для определения параметров МЛР (как парной, так и множественной регрессии), а вторая – для вывода любой точки или множества точек, принадлежащих уравнению модели y^*(х_i) (также в общем случае для множественной регрессии). Эти функции относятся к категории «Статистические», после их активизации появляются диалоговые окна, приведенные на рис.2.9 и 2.10. Ввод исходных данных для этих функций одинаков: в окне «Известные значения у» помечается диапазон входных данных показателя (например, b2:b11 – ввод данных, записанных в 10 ячеек столбца В с номерами строк от 2-й по 11-ю), после чего в окне «Известные значения х» аналогично помечается диапазон входных данных фактора (например, с2:с11).

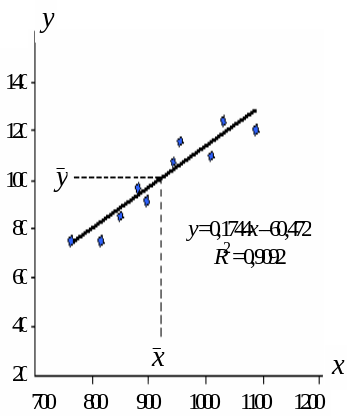
Рис.2.7

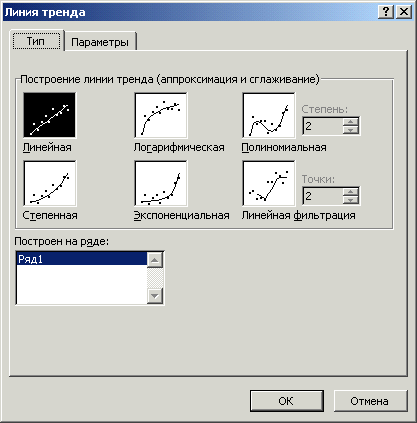
Рис.2.8

Если до ввода (и вызова функций) на рабочем листе электронной таблицы выделить поле выходных данных (результат решения одной из задач) и нажать клавишу «=» (в левой ячейке появится знак «=»), то после ввода данных и одновременного нажатия клавиш Shift – Ctrl – Enter выделенное поле будет заполнено результатами расчетов. Например, при использовании функции «ЛИНЕЙН» при парной регрессии помечается строка из двух ячеек, ввод формулы инициируется нажатием клавиши «=», вызывается функция «ЛИНЕЙН», вводятся данные, после чего нажимаются три клавиши Shift – Ctrl – Enter, и в нашем примере получим значения параметров модели

0,174426

– 60,4723.

Подчеркнем, что параметры модели функции «ЛИНЕЙН» выводятся в обратном порядке, справа налево: b₁ = а = – 60,4723, b₂ = b = 0,174426 (при множественной регрессии далее выводятся b₃, b₄ и т.д.).

Функция «ТЕНДЕНЦИЯ» может использоваться для расчета значений y^*(х_i) = y^*_i , необходимых для вычисления остатков регрессии e_i = y^*_i – y_i, а также для прогноза показателя у_р = y^*(х_р) в новой задаваемой точке прогноза х_р. В первом случае в электронной таблице помечается поле выходных данных (скажем, столбец из 10 ячеек h2:h11), нажимается клавиша «=», вызывается функция «ТЕНДЕНЦИЯ» и вводятся данные, после этого при нажатии клавиш Shift – Ctrl – Enter в помеченном столбце появляются результаты расчета y^*_i (в нашем примере – колонка y^*(х_i) таблицы 2.2). Если необходимо найти прогноз у_р = y^*(х_р = 1150м²), то в третье окно функции «ТЕНДЕНЦИЯ» («Новые значения х») вводим точку прогноза 1150, и за чертой входных данных читаем результат прогноза показателя {140, 11807498601}. Этот же результат можно получить по формуле у_р = y^*(1150) = – 60,4723 + 0,1744·1150 (с малой ошибкой за счет округления). Если задать несколько точек прогноза, то в результате выводится вектор средних значений показателя в этих точках y^*(х_рk).

В примере 2.3 нам осталось определить доверительный интервал прогноза с вероятностью 0,68 (t = 1). Оценка СКО ошибок модели согласно (2.35) и расчетных значений таблицы 2.2 равна

Тогда в соответствии с (2.41 – 2.42) граничная ошибка прогноза показателя

и доверительный интервал этого прогноза определяется границами

у_р [140,12 – 7,58; 140,12 + 7,58] = [132,54; 147,7].

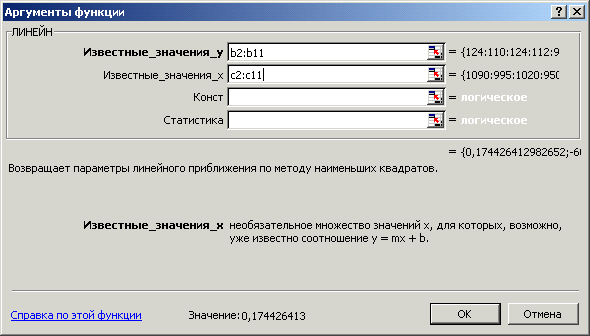
Рис.2.9

Рис.2.10

Итак, с вероятностью 0,68 при торговой площади 1150м² прогнозируемые значения товарооборота фирмы лежат в пределах приблизительно от 133 до 148 тыс. грн. Относительная точность этого прогноза составляет величину 7,58/140,12  0,05 или около 5%. При доверительной вероятности 0,95 интервал расширится вдвое и относительная точность снизится до приблизительно 10%. Можно лишь условно доверять данному прогнозу, так как небольшая выборка не дает достаточных оснований для нормального распределения оценок и ошибок.