Контрольные вопросы

1. Для какого типа моделей наиболее характерно свойство автокорреляции? Почему?

2. Приведите типовые графики зависимостей остатков регрессии, для которых характерна положительная и отрицательная автокорреляция (первого порядка).

3. Что можно предпринять для уменьшения автокорреляции?

4. Что такое автокорреляционная функция остатков? Как определяется выборочный коэффициент автокорреляции первого порядка?

5. Опишите случайный регрессионный процесс первого порядка. Какие параметры необходимо знать для задания процесса?

6. В чем специфика обобщенного метода наименьших квадратов по сравнению с МНК? Что необходимо знать для применения ОМНК?

7. Как определяется вектор оптимальных ОМНК оценок параметров модели линейной регрессии? Докажите, что при выполнении свойств гомоскедастичности и некоррелированности ошибок ОМНК оценки параметров модели превращаются в МНК оценки.

8. В чем суть итерационной процедуры Кохрейна-Оркотта определения параметра регрессионного процесса первого порядка?

9. Какие параметры используются при проверке гипотезы о наличии автокорреляции методом Дарбина-Уотсона?

10. Опишите процедуру тестирования Дарбина-Уотсона на наличие автокорреляции в модели линейной регрессии.

6. Двухмерная модель нелинейной регрессии

В ряде случаев линейные модели не могут достаточно точно отображать реальные взаимосвязи между показателем и факторами. При расширении области определения факторов обычно наблюдаются переходы в экстремальные точки, области насыщения показателя и другие нелинейные явления. Хорошей иллюстрацией этого могут служить сезонные колебания спроса на различные товары (прохладительные напитки, купальники, лыжи, шубы и пр.). В таких случаях приходится обращаться к нелинейным моделям, которые оказываются более точными по сравнению с линейными. При этом говорят, что такая модель более адекватно отображает реальные взаимосвязи явлений. Правда, большей точности можно достичь лишь при правильном выборе типа нелинейной функции. Другими словами, возникает новая задача подбора аппроксимирующей функции, при которой функционал ошибок минимален (среди известных или протестированных функций).

Для простоты иллюстраций мы здесь рассмотрим лишь парную регрессию. В общем случае спецификация двухмерной модели (с одним фактором Х) имеет вид

y_i =  (, x_i) + _i, i = 1, 2,…, n, (6.1)

где  = (₁, ₂,..., _m) – m-мерный вектор параметров модели;

у^* = (, x) – модель (как правило, одна из элементарных математических функций);

_i – случайная ошибка моделирования.

При m = 2 имеем двухмерную двухпараметрическую модель, для которой удается применить метод линеаризации (сведение нелинейной модели к линейной с помощью замены переменной – функции от фактора). При m > 2 линеаризация при парной регрессии невозможна и построение модели существенно усложняется. Для иллюстрации этого рассмотрим трехпараметрическую модель, описываемую параболой.

6.1. Трехпараметрическая парабола

Одной из распространенных аппроксимирующих функций является степенной многочлен (полином) (m–1)-й степени

(, х) = ₀ + ₁х + ₂х² + ₃х³ +…+ _m-1х^{m – 1}, _{m – 1}  0,

определяемый m параметрами. В частности, линейная модель описывается полиномом 1-й степени и двумя параметрами: ₀ и ₁ (или а и b). Полином второй степени дает трехпараметрическую параболу, которую запишем в виде

(, х)= ₀ + ₁х + ₂х²,  = (₀, ₁, ₂). (6.2)

Здесь параметр ₀ является постоянной составляющей модели, ₁ – коэффициент линейной регрессии, ₂ – коэффициент квадратичной регрессии. Определим оценки параметров  модели с остатками регрессии

e_i = y_i^*– y_i= ₀ + ₁х_i + ₂х_i² – y_i, (6.3)

используя метод наименьших квадратов (МНК). Дифференцируя функционал ошибок по оптимизируемым параметрам ₀, ₁, и ₂ получим

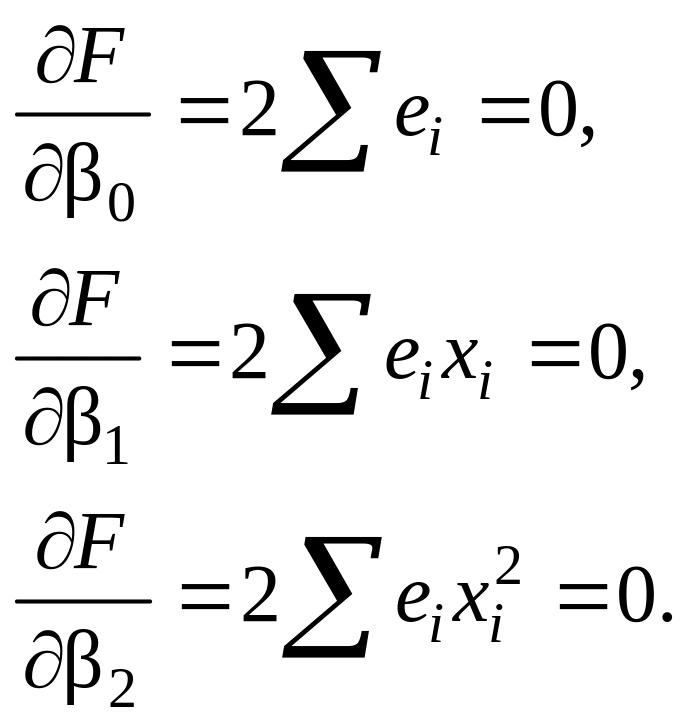
Выразим уравнения системы через выборочные данные и параметры (6.3), обозначая решения системы уравнений как оценки МНК :

(6.4)

Умножим первое уравнение системы на , второе – на n и вычтем из второго первое, тогда

(6.5)

Аналогичные преобразования первого и третьего уравнений (с умножением первого на ) дают

(6.6)

Исключив, таким образом, постоянную составляющую а, получили систему из двух уравнений относительно неизвестных параметров b и c, которая легко решается. Обозначим

(6.7)

В матричной форме (6.5), (6.6) теперь можно переписать

Отсюда методом обращения матрицы получаем оценки МНК параметров

(6.8)

После определения коэффициентов линейной и квадратичной регрессии находим постоянную составляющую из (6.4)

(6.9)

Из (6.8) следует, что МНК оценки параметров параметрической модели существуют при выполнении (АС – В²)  0. Вырожденный случай (АС – В²) = 0 возникает, в частности, при выборке с одинаковыми элементами x_i = g = const, что не представляет практического интереса.

Пример 6.1. Пусть объем продаж Y (у.е.) сезонной обуви в последнем и первом кварталах года по месяцам (Х = 1, 2,…,6) описывается данными таблицы 6.1 (1 – октябрь, 2 – ноябрь и т.д.). Требуется определить МНК оценки параметров трехпараметрической параболической модели тренда сезонной продажи зимней обуви.

Таблица 6.1

i	1	2	3	4	5	6	
Y	4	6	6	5	2	2	25
X	1	2	3	4	5	6	21
X2	1	4	9	16	25	36	91
X3	1	8	27	64	125	216	441
X4	1	16	81	256	625	1296	2275
YX	4	12	18	20	10	12	76
YX2	4	24	54	80	50	72	284

Определим сначала вспомогательные величины (6.7)

Так как детерминант матрицы АС – В² = 23520, то коэффициенты регрессии (6.8) равны

Постоянную составляющую определяем с помощью (6.9)

Следовательно, уравнение модели описывается параболой

y^* = 2,8 + 2,09286x – 0,39286x².

Эта зависимость приведена на рис. 6.1 (сплошная линия). Она гораздо точнее отображает тенденцию (тренд) объема продаж сезонной обуви по сравнению с линейным трендом (штриховая линия). На рис.6.1 также представлены точки выборки (x_i, y_i).

Рис.6.1

Определим остатки регрессии (ошибки) квадратичной модели:

Суммарная ошибка близка к 0 (она равна – 2·10 ^{– 4} в связи с ошибками округления для параметров модели). Функционал ошибок (или сумма квадратов ошибок)

Cравним эти результаты с ошибками для МЛР. Её параметры согласно (3.8), (3.6)

Для этой модели, представленной штриховой линией на рис.6.1, ошибки равны:

е₁ = 6,466667 – 0,657143x₁ – у₁ = 1,809524,

е₂ = 6,466667 – 0,657143x₂ – у₂ = –0,847619,

е₃ = 6,466667 – 0,657143x₃ – у₃ = –1,504762,

е₄ = 6,466667 – 0,657143x₄ – у₄ = –1,161905,

е₅ = 6,466667 – 0,657143x₅ – у₅ = 1,180952,

е₆ = 6,466667 – 0,657143x₆ – у₆ = 0,523810.

Функционал ошибок равен

Таким образом, квадратичная модель позволяет уменьшить СКО в данном примере в 1,625 раз по сравнению с МЛР. Хотя это убедительный результат, нельзя считать решенной задачу выбора модели (возможно, существует трехпараметрическая модель с меньшей СКО). Можно лишь утверждать, что параболическая модель значительно точнее аппроксимирует выборочные данные примера 6.1, чем простая линейная модель.

Оценки МНК параметров трехпараметрической параболы легко определяются с помощью научного калькулятора CASIO (типа fx-82TL, fx-82W) в режиме вычисления регрессии REG – QUAD (квадратическая регрессия). После очистки памяти и ввода данных они сразу выводятся на дисплей нажатием клавиш SHIFT-A, SHIFT-B, SHIFT-C (см. руководство по пользованию). Кроме того, можно найти прогнозное значение показателя заданием точки прогноза х_р и последовательным нажатием клавиш SHIFT- , после чего на дисплее отображается значение прогноза. Можно также вывести все промежуточные результаты расчетов (y_i, x_{i ,}x_i², x_i³, x_i⁴ y_ix_i, y_ix_i² и др.), средние значения и среднеквадратичные отклонения величин.