4.1. Выражение для оценки параметров млр в стандартизованной форме

Вспомним, что многие распределения в математической статистике опираются на понятие стандартной нормальной случайной величины Z  N(0,1) c нулевым средним и единичной дисперсией, что обеспечивается центрированием и нормировкой любой нормальной величины Х:

z = (x – M[X])/_x.

Для выборочных данных стандартизацию следует осуществлять с использованием выборочных средних показателя и факторов

и выборочных дисперсий

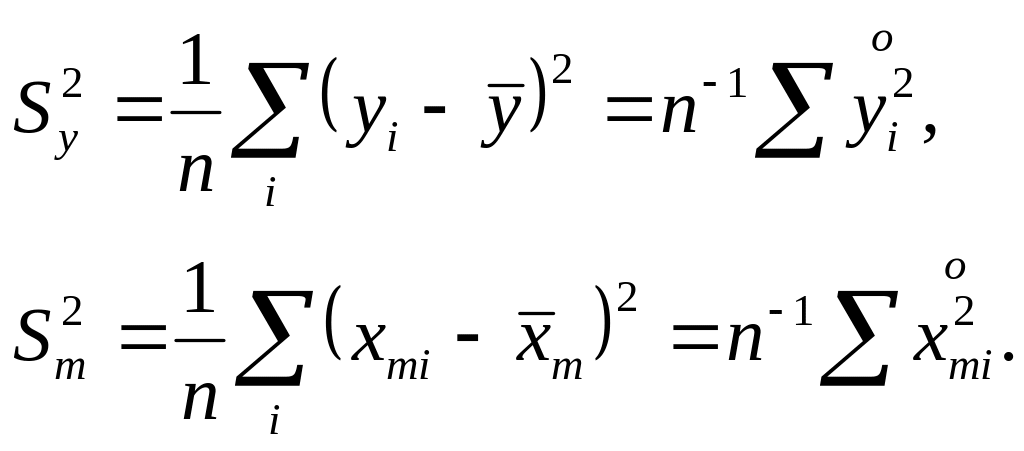(4.1)

Перепишем систему уравнений (3.15) для отклонений

Разделим каждое уравнение на после чего каждое слагаемое правой части умножим и разделим на S_m, m = 2, 3,…, k, так что

(4.2)

Введем обозначения для входящих сюда величин

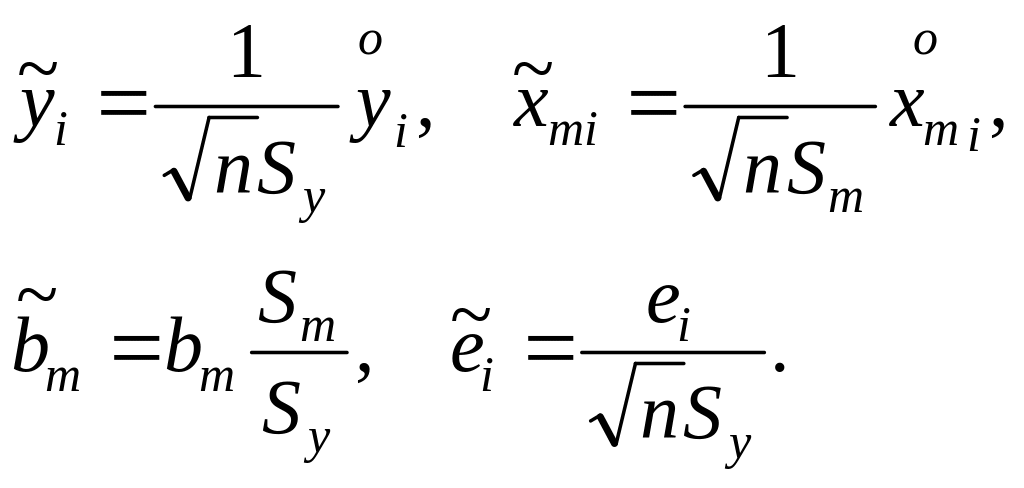(4.3)

Запишем теперь (4.2) в матричной форме

аналогичной соотношению (3.15) для ненормированных отклонений. С помощью метода наименьших квадратов нетрудно теперь получить подобную (3.16) оценку МНК нормированных (безразмерных) параметров модели

(4.4)

Входящие в правую часть векторы и матрицы имеют безразмерные элементы, нормированные к максимальным значениям. В частности, множитель

= (r_yx2, r_yx3, …, r_yxk) (4.5)

является (k – 1)-мерным вектором-строкой коэффициентов корреляции между показателем Y и факторами Х₂, Х₃, …, Х_k. Из (4.3), (4.4) нетрудно получить

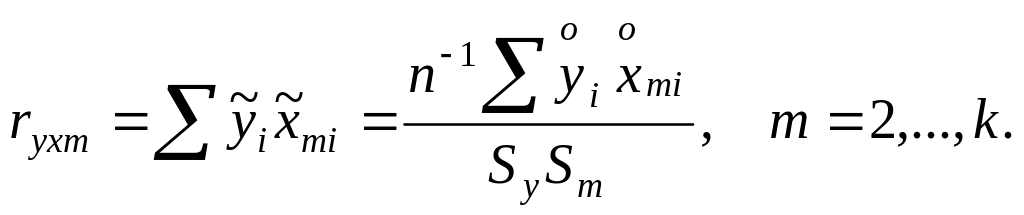(4.6)

Матрица справа в (4.4) является обратной по отношению к корреляционной матрице факторов размерности (k – 1)(k – 1)

(4.7)

Её элементами являются коэффициенты корреляции между факторами, равные согласно (4.3)

(4.8)

Напомним, что коэффициенты корреляции между случайными величинами принимают значения от –1 до 1. В частности, диагональные элементы матрицы (4.7) r_ii = 1. С учетом введенных обозначений оценка (4.4) параметров модели выражается через вектор коэффициентов корреляции между показателем и факторами (5.5) и корреляционную матрицу факторов (4.7) как

(4.9)

После определения оценок нормированных параметров денормировка согласно (4.3) осуществляется с помощью преобразования

(4.10)

Пример 4.1. Рассмотрим трехмерную модель для выборки из 5 точек, в которой уровень годовой инфляции Y (%) в 5 странах рассматривается в зависимости от уровня годового валового национального продукта (ВНП) на душу населения Х₂ (у.е.) и природных ресурсов страны Х₃ (оценивается в баллах по 10-балльной шкале) согласно таблице 4.1.

Согласно (4.6) с учетом (4.1) получим коэффициенты корреляции между показателем и факторами

Таблица 4.1

i	1	2	3	4	5	/n
Y, %	4	7	7	8	9	7
X2, y.e.	8	4	3	3	2	4
X3, баллы	5	5	4	1	5	4
	-3	0	0	1	2	0
	4	0	-1	-1	-2	0
	1	1	0	-3	1	0
	9	0	0	1	4	14/5
	16	0	1	1	4	22/5
	1	1	0	9	1	12/5

В данном случае трехмерной модели достаточно рассчитать один элемент корреляционной матрицы между факторами Х₂ и Х₃. Согласно (4.8)

Корреляционная матрица факторов при этом имеет вид

.

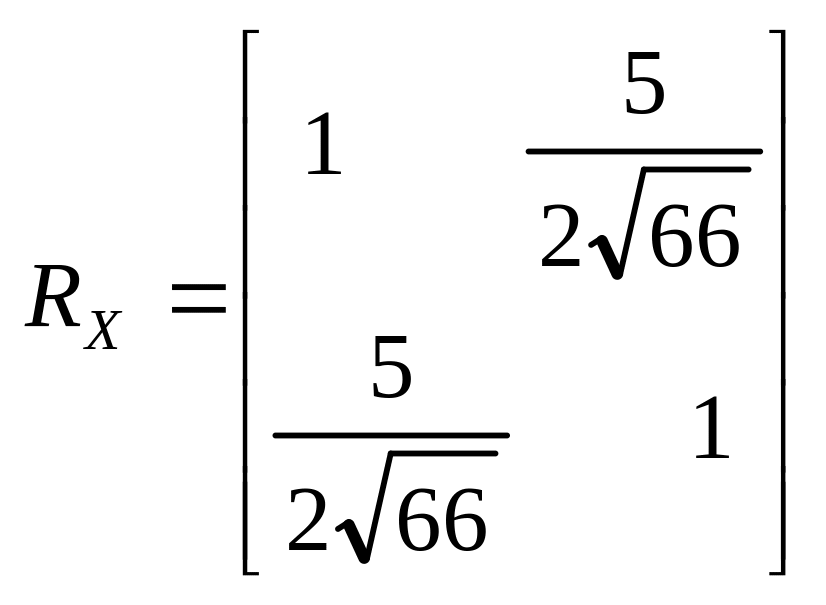Определитель корреляционной матрицы равен

Итак, обратная к R_Х матрица имеет вид

Нормированные параметры (4.9) модели равны

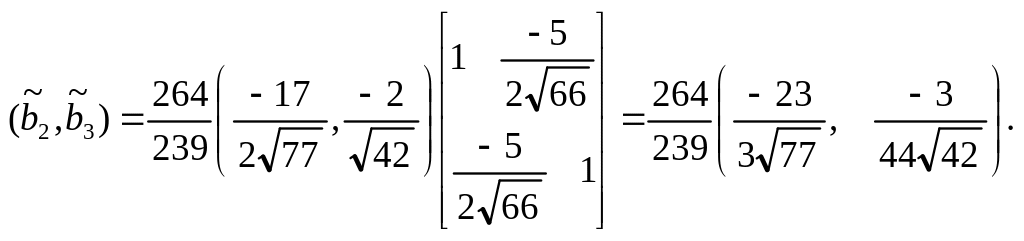
Денормировка согласно (4.10) дает

Далее находим постоянную составляющую модели

Эти же результаты можно получить с помощью формулы (3.16), выраженной через отклонения. Действительно,

Как видим, коэффициенты регрессии совпадают с предыдущим расчетом. Достоинством расчета в стандартизованной форме является наличие информации о коэффициентах корреляции как между факторами, так и между показателем и факторами. В частности, Это сравнительно невысокая корреляция, поэтому нет оснований для проверки на мультиколлинеарность. В других случаях следует пользоваться более строгими методами статистической проверки гипотез.