8.8. Движение одиночных капель и пузырьков

8.8.1. Методы подобия и размерностей

В механике двухфазных систем числа подобия могут быть представлены как мера отношения сил, действующих на единицу площади поверхности:

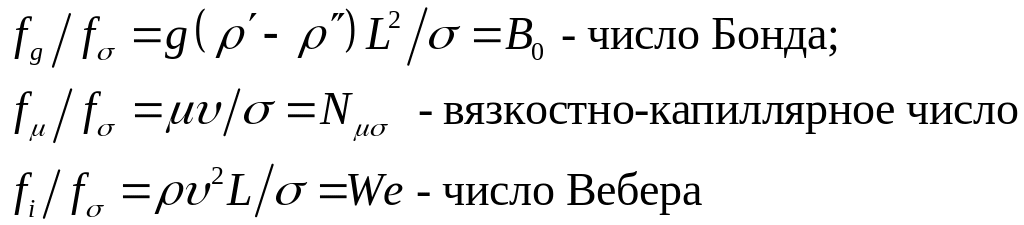( 8.80)

(8.81)

(8.82)

где , , , – соответственно силы поверхностного натяжения, гравитационные (архимедовы), инерции и вязкости;

– характерный размер системы;

– динамическая вязкость жидкости;

– коэффициент поверхностного натяжения;

и – плотность жидкости и газа;

– характерная скорость;

– ускорение силы тяжести.

Число Рейнольдса можно представить как отношение сил – инерции и вязкости . Число Фруда можно представить, как отношение силы инерции к силе тяжести

– для двухфазных систем, если в жидкости движется газовый пузырек.

– если капля движется в газе.

При анализе движения дискретной капли (частицы) в сплошной среде коэффициент сопротивления используется как число подобия в виде:

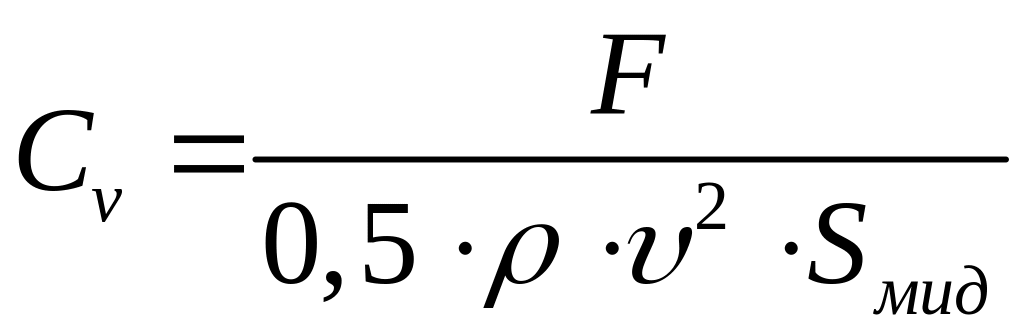(8.83)

где – сила вызывающая движение;

– площадь миделевого сечения частицы. Например, при движении в жидкости сферического пузырька коэффициент сопротивления аналогичен по физическому смыслу числу Фруда

(8.84)

При анализе двухфазных систем часто используется безразмерное число, содержащее лишь свойства фаз и ускорение свободного падения:

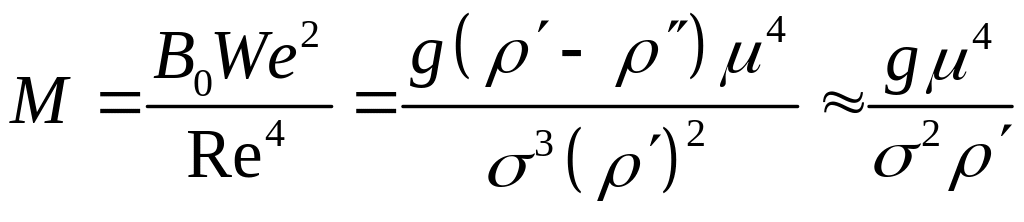(8.85)

С помощью чисел подобия процесс движения пузырьков можно описать уравнением вида:

(8.86)

или

(8.87)

Причем, во многих случаях движение дискретной фазы (внутри пузырька или капли) оказывается несущественным, так что симплексы , в анализе не учитываются.

Конкретный вид уравнения подобия может быть получен на основе опытных результатов, а в отдельных случаях и теоретически.

Силы поверхностного натяжения стремятся придать пузырьку (капле) сферическую форму, а остальные силы стремятся его деформировать.

Первое условие характерно для задач гидростатики, последнее – для движущихся капель и пузырьков (достаточное условие сферичности).

При анализе размерностей всегда следует думать о физической полноте набора независимых параметров и переменных процесса. Иначе можно получить формально верный, но физически ошибочный результат.

В качестве примера приведем эмпирическую формулу для скорости свободного всплытия газового пузыря в жидкости, когда эта скорость снижается с увеличением радиуса пузыря:

(8.88)

где – скорость всплытия пузыря, м/с;

– коэффициент поверхностного натяжения, Н/м;

– плотность жидкости, кг/м³;

– радиус эквивалентной по объему сферы, м.

В формуле (8.88) размерности согласованы:

.

Однако в ней отсутствует подъемная сила – единственный источник движения пузыря. Следовательно, независимо от действия гравитации пузырь по этой формуле всегда будет всплывать с одной и той же скоростью, даже в невесомости.

В рамках анализа размерностей можно предположить, что:

а) определяемым критерием подобия является отношение масштаба динамического сопротивления подъему пузыря в жидкости к масштабу силы Архимеда:

где – ускорение свободного падения, м/с²;

– плотность газа, кг/м³;

б) коэффициент гидравлического сопротивления представляет собой функцию деформации пузыря, характеризуемого отношением силы поверхностного натяжения и той же силы Архимеда. Безразмерное соотношение этих воздействий можно записать в форме:

где – мера давления, создаваемая поверхностным натяжением, Н/м².

8.8.2. Скорость движения капли и пузырька при Re<1

При малых числах Рейнольдса уравнение Навье–Стокса для несжимаемой жидкости упрощается, ибо в нем можно опустить инерционный член .

В таком приближении было получено решении задачи о движении сферической капли в вязкой жидкости при .

Решение дает поля скоростей во внешней области и внутри капли, а также значения нормальных и касательных напряжений на границе капли. Интеграл от проекций этих напряжений на направление движения можно рассматривать как силу сопротивления:

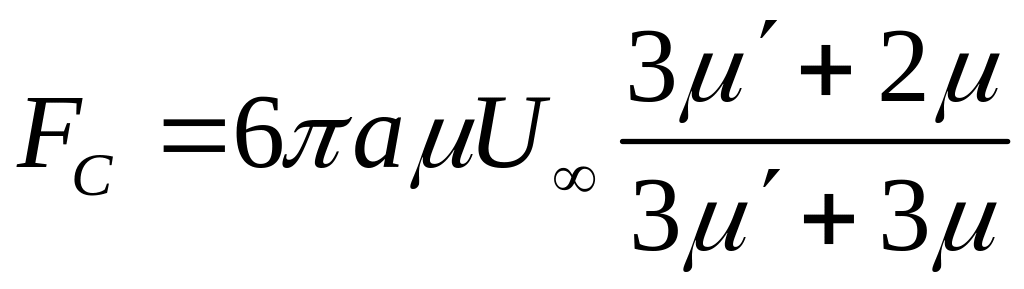(8.89)

где – радиус капли;

– скорость движения;

, – динамическая вязкость жидкости вне и внутри капли соответственно.

Если , то (8.86) переходит в формулу Стокса для обтекания твердой сферы при :

(8.90)

Для капли, движущейся в жидкости под действием Архимедовой силы , равенство дает скорость её установившегося падения (всплытия):

(8.91)

Для твердой сферы и скорость падения равна:

(8.92)

где – плотность твердой фазы.

В маловязких жидкостях (вода, керосин, спирты и т.п.) в газах условию подчиняется движение очень малых твердых частиц (диаметром не более 0,1 мм). Для газовых пузырьков в жидкости , так что:

(8.93)