3.5. Расход и средняя скорость потока

Поток представляет собой совокупность элементарных струек (рис. 3.6).

Рис. 3.6

Из рис. 3.6 видно, что скорость в отдельных струйках различна.

Расход потока Q равен сумме расходов элементарных струек, т.е.

. (3.2)

Скорость движения потока характеризуется средней скоростью в данном поперечном сечении:

(3.3)

или уравнение расхода . (3.4)

3.6. Условие неразрывности, или сплошности движения жидкости

Для двух сечений 1–1 и 2–2 элементарной струйки в устано­вив­шемся движении (рис. 3.7) можно записать:

.

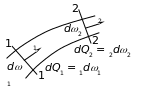
Рис. 3.7

Видно, что dQ₁ > dQ₂ по условию несжимаемости и dQ₁ < dQ₂ по условию сплошности движения.

Следовательно, условие неразрывности имеет вид dQ₁ = dQ₂ или u₁d₁ = u₂d₂.

Очевидно, что для всего потока имеем

_{1 1} = _{2 2}

или

.

Таким образом, при установившемся движении жидкости расход в любом сечении потока остается неизменным.

3.7. Методы исследования движения жидкости

Существует два метода изучения движения жидкости: метод Ла­гранжа и метод Эйлера.

Метод Лагранжа изучает изменение положения в пространстве отдельных частиц жидкости, т.е. траектории их движения.

Метод Эйлера изучает поле скоростей, т.е. картину движения частиц жидкости в отдельных точках пространства в данный момент времени.

Метод Лагранжа в гидродинамике используется редко, ввиду его сложности. Обычно изучение движения основано на методе Эйлера, суть которого заключается в следующем.

Метод основан на понятии местной скорости или скорости в точке в данный момент времени.

В общем случае местные скорости различны в один и тот же момент времени (рис. 3.8) в разных точках. Они могут изменяться во времени в каждой точке.

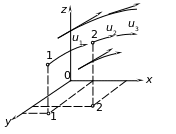
Рис. 3.8

Проекции скорости на оси координат можно записать в виде функций:

(3.5)

Функция (3.5) характеризует поле скоростей движущейся жид­кости.

Используя метод Эйлера, можно выразить ускорение а жидкой частицы в соответствии с физическим смыслом:

.

Если учесть, что для движущейся частицы ее координаты яв­ляются функциями времени:

,

то проекции скорости будут сложными функциями времени:

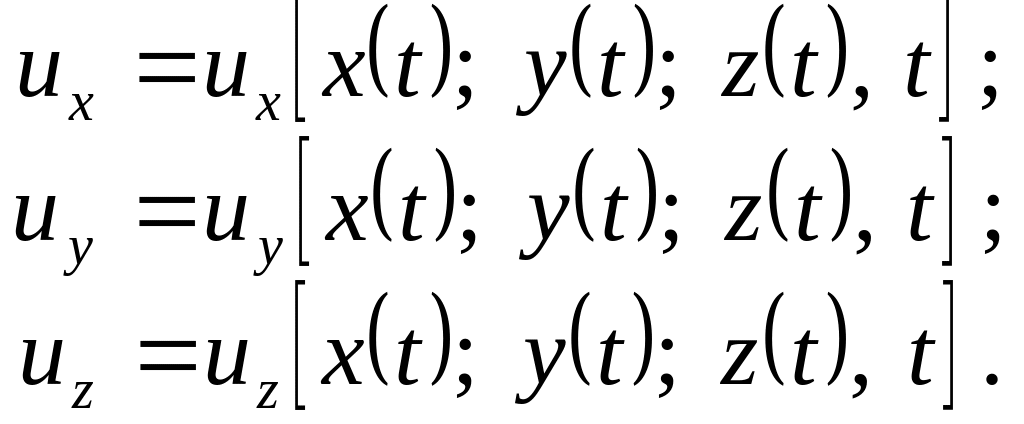
Используя правило дифференцирования сложных функций, для проекций полного ускорения получим:

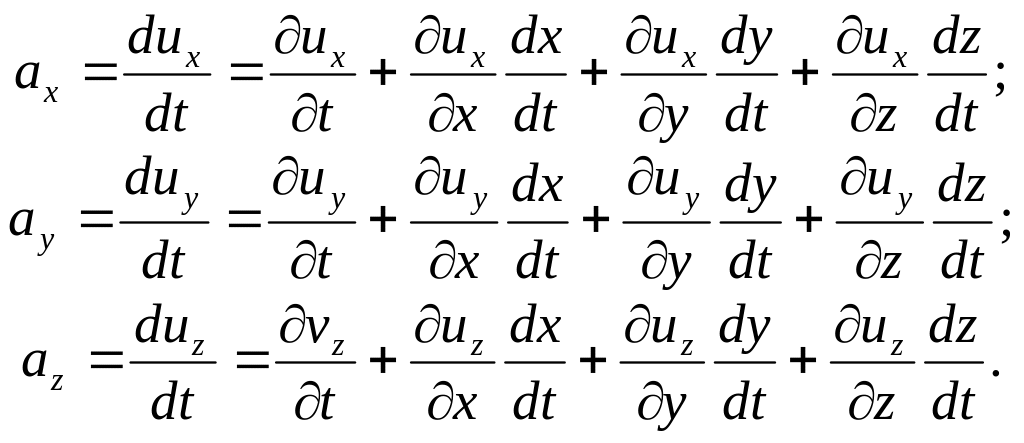(3.6)

Учитывая, что для движущейся жидкости

,

преобразуем функции (3.6) к виду:

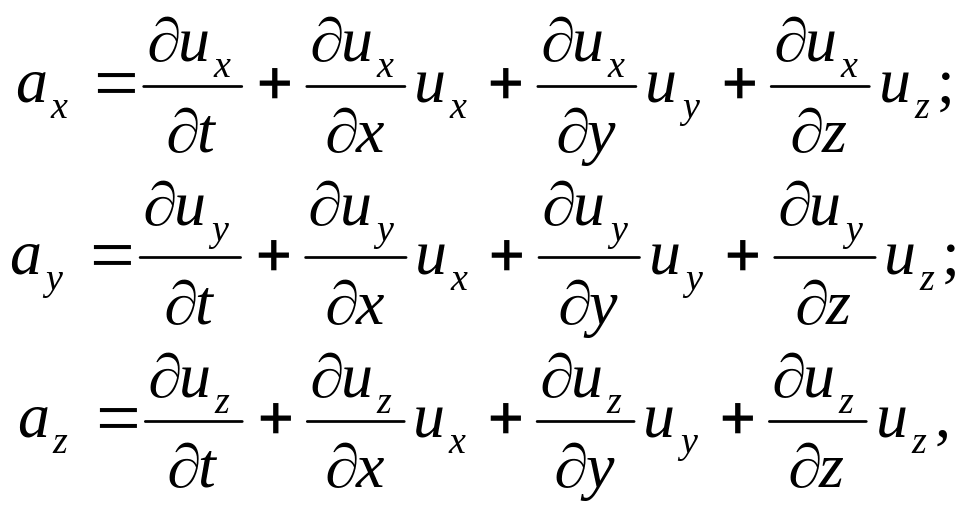(3.7)

где ; ; – индивидуальные или субстанциональные производные;

; ; – локальные производные, выражающие из­­менение во времени вектора u в фик­си­рованной точке пространства;

– конвективная производная вектора u. Эта величина выражает изменение ско­рос­ти в пространстве в данный момент вре­мени. При установившемся движении локальные ускорения равны нулю.

3.8. Уравнение Эйлера

По основному закону механики равнодействующая всех внешних сил, действующих на данное тело, равна массе тела, умноженной на ускорение, с которым движется это тело:

. (3.8)

Выделим в потоке жидкости элементарный объем в форме па­рал­ле­лепипеда (рис. 3.9) и запишем основное уравнение (3.8) в про­екциях по осям:

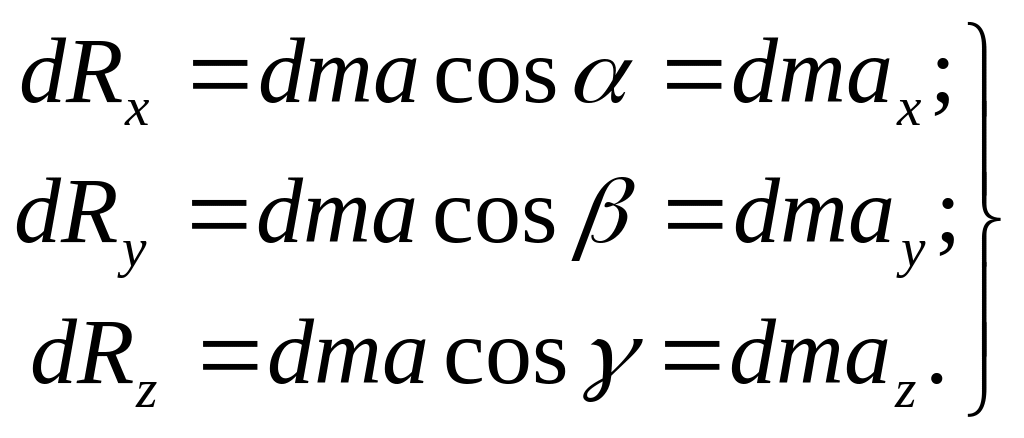(3.9)

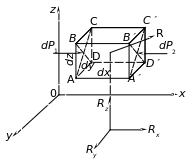
Рис. 3.9

Для первого уравнения (3.9) найдем массу

.

Ускорение вдоль оси Ох равно первой производной скорости по времени t, т.е. :

.

Учитывая, что ,

где ,

получим

. (3.9а)

На выделенную элементарную массу действуют поверхностные силы давления и объемные силы (или массовые), т.е. в силу dR_x включаются эти силы.

Рассмотрим проекцию силы давления на боковую грань АВСD и А¢В¢С¢D¢:

,

где р и р –

среднее гидростатическое давление для указанных граней:

.

Тогда . Сила dP₂ войдет в основ­ное уравнение со знаком «минус», т.е. в сумму проекций сил дав­ления на боковые грани:

. (3.10)

Проекция объемной силы dFx определяется выражением:

, (3.11)

где Х – проекция ускорения объемной силы;

 – плотность жидкости;

dxdydz = dV – объем параллелепипеда.

Проекция равнодействующей с учетом выражений (3.10) и (3.11) имеет вид:

. (3.12)

Подставляя выражение (3.9а) в уравнение (3.12), получим:

.

После сокращения на , т.е. отнеся уравнение к единице массы, получим:

. (3.13)

Аналогично составив выражения для сил dRy и dRz и для dma_y и dma_z, получим три уравнения Эйлера:

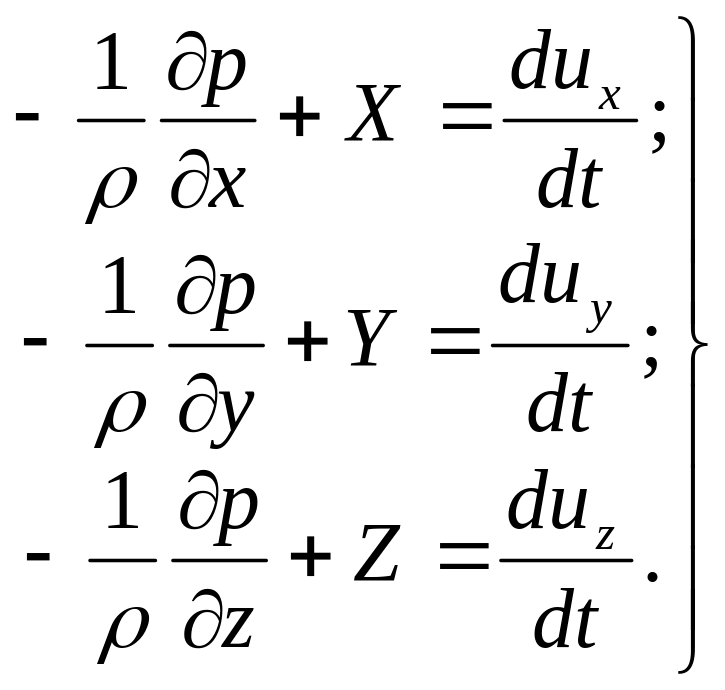(3.14)

Система (3.14) описывает движение как капельной, так и га­зообразной жидкости. В системе 3-х уравнений пять неизвестных u_х, u_у, u_z, p и , поэтому необходимо иметь еще два уравнения. Такими уравнениями являются уравнения неразрывности и ха­рактеристическое уравнение.

При (для капельной жидкости) достаточно уравнения неразрывности:

.