3.13. Потери напора при равномерном движении

Рассмотрим равномерное движение в трубопроводе при следую­щих условиях:

1. Ускорение потока равно нулю, следовательно, силы инерции отсутствуют.

2. Средние скорости во всех поперечных сечениях одинаковы.

3. Местные сопротивления отсутствуют. Существуют сопротив­ле­ния по длине, вызывающие соответствующие потери напора на трение (рис. 3.16).

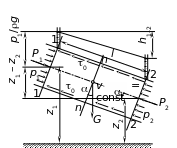
Рис. 3.16

4. Закон распределения давления между сечениями 1–1 и 2–2 подчиняется гидростатическому, т.е.

.

5. На объём жидкости между сечениями 1–1 и 2–2 действуют силы внешнего давления Р₁ и Р₂ (Р = р), сила тяжести и сила сопротивления движению .

Пользуясь принципом Д’Аламбера, напишем уравнение дина­ми­ческого равновесия для массы жидкости, заключённой между сече­ниями 1–1 и 2–2 на оси х:

. (3.29)

В состав активных сил входят:

1. Сила земного притяжения , проекция которой на ось х равна:

.

Так как , то получаем

. (3.30)

2. С учётом допущения п. 4, равнодействующие сил давления Р₁ и Р₂ приложены в центрах тяжести сечений 1–1 и 2–2 и равны:

и .

Тогда сумма проекций на ось х

. (3.31^)

3. Нормальные силы к оси х равны и противоположно направ-ле­ны, поэтому проекции сил N...N равны нулю.

Очевидно, что левая часть уравнения (3.30) составляет две силы, а именно:

. (3.32)

Силы сопротивления F_сопр определяются по касательным напря­жениям на стенке канала. Эти силы направлены параллельно оси потока в сторону, обратную движению жидкости.

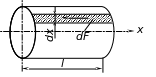
Рис. 3.17

Обозначим силу сопротивления на элементарную площадку d через dF, тогда для участка трубы имеем:

. (3.33)

После интегрирования, принимая ( может изме-няться по периметру) в выражении (3.33), получим

, (3.34)

где 0 –

среднее значение касательного напряжения на стенке.

С учётом уравнений (3.32) и (3.34) запишем уравнение динами­чес­кого равновесия в виде

. (3.35)

Разделив члены уравнения (3.35) на , получим

. (3.36)

Обозначим отношение , после преобразования выражения (3.36), имеем

. (3.37)

Сравним уравнение Бернулли, записанное для сечений 1–1 и 2–2:

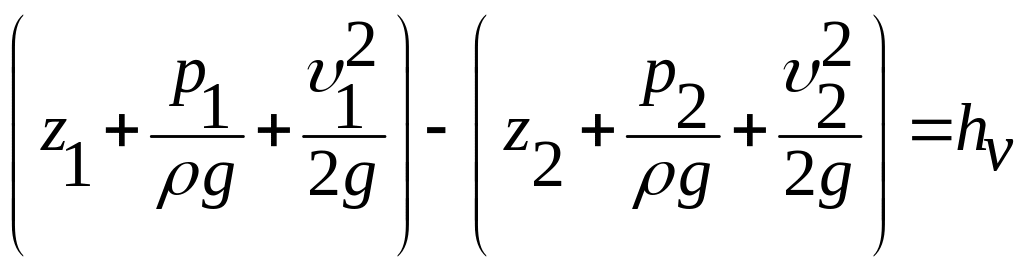. (3.38)

Так как при равномерном движении , то из сопоставления уравнений (3.37) и (3.38) находим

. (3.39)

Учитывая, что (где i – гидравлический уклон), преоб­ра­зуем выражение (3.39) к виду

или . (3.40)

Это уравнение академик Н.Н. Павловский назвал основным урав­нением равномерного движения.

Опытным путём Шези установлено, что величина пропор­цио­нальна квадрату скорости, т.е.

, (3.41)

где  –

коэффициент пропорциональности, в общем случае вели­чи­на переменная.

Подставим равенство (3.41) в выражение (3.39), получим фор­мулу Вейсбаха

.

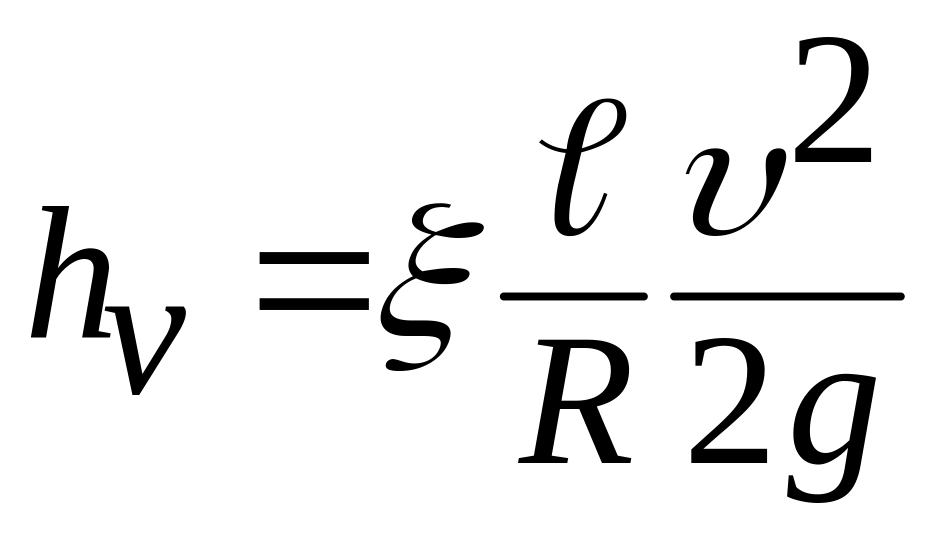Учитывая, что , преобразуем формулу Вейсбаха к виду

.

Обозначим , получим

, (3.42)

где  –

коэффициент гидравлического трения.

Формула (3.42) именуется формулой Дарси-Вейсбаха. Она ис­поль­зуется для расчёта трубопроводов.

Учитывая, что и 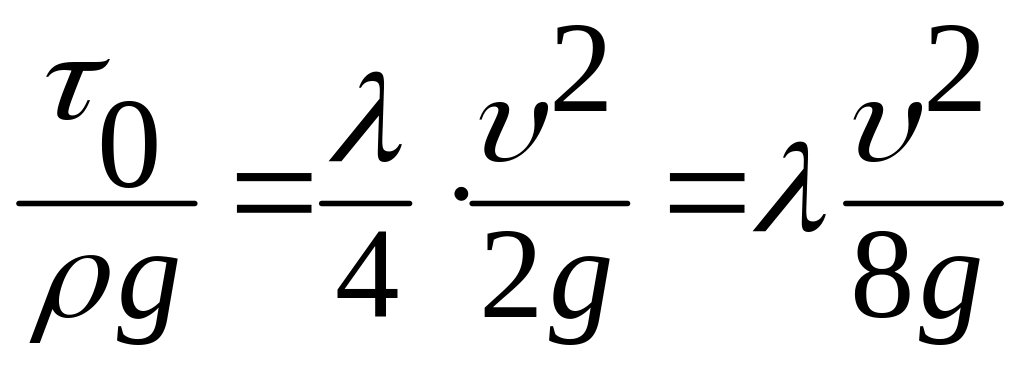, получим

.

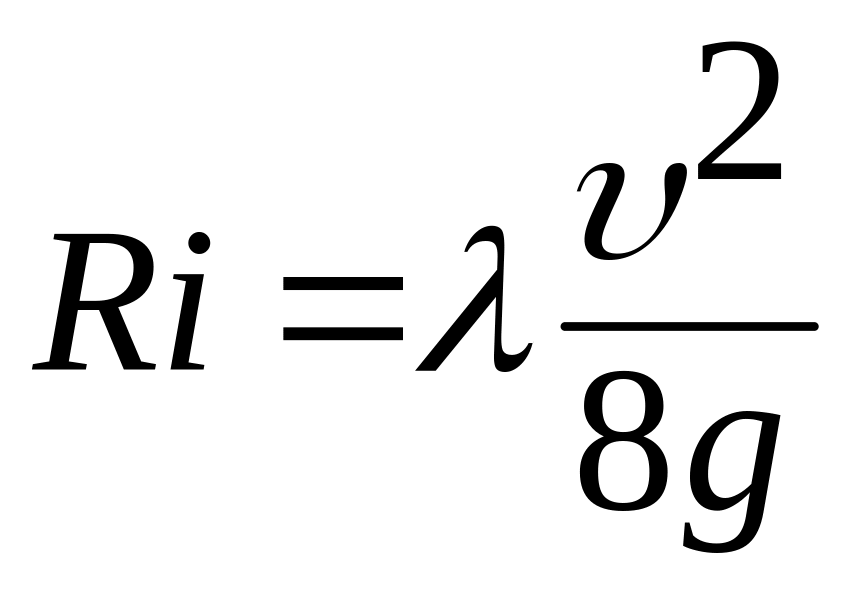Отсюда

.

Обозначив , м/с, получим формулу Шези

,

где С – коэффициент Шези.

Формула Шези получила широкое применение в расчётах от­крытых потоков.

Анализ формулы (3.42) показывает, что потери пропор­цио­наль­ны квадрату скорости, а закон сопротивления называется законом квадратичного сопротивления.

В то же время установлено, что потери напора, помимо скорос­ти, зависят от характера режима, формы и размеров сечения, вяз­кос­ти жидкости, материала и состояния стенок.

Это не учитывается формулами Шези и Дарси-Вейсбаха.

На графике (рис. 3.18) показана зависимость потерь на трение в зависимости от скорости движения жидкости . Однако квад­ратичные формулы Шези и Дарси-Вейсбаха очень удобны для практических целей и обычно применяются как для турбулентного, как и для ламинарного режимов течения жидкости.

Рис. 3.18

Отклонения от квадратичного закона учитываются тем, что коэффициенты  и С ставятся в косвенную зависимость от скорости. Поэтому основная задача при определении потерь на трение при равномерном движении жидкости сводится к определению коэф­фи­циентов  и С при известной скорости движения жидкости.