Коэффициент скорости при совершенном сжатии

8.3. Коэффициенты:ε, ζ, φ, μ

В уравнении Бернулли для идеальной жидкости из-за отсутствия вязкости нет потерь на трение, и коэффициенты сопротивления равен ξ = 0, при α = 1, φ = 1. Скорость истечения идеальной жидкости из отверстия с острой кромкой

.

Коэффициент скорости φ для реальной вязкой жидкости можно определить, поделив скорость истечения реальной жидкости в сжатом сечении на скорость истечения идеальной жидкости.

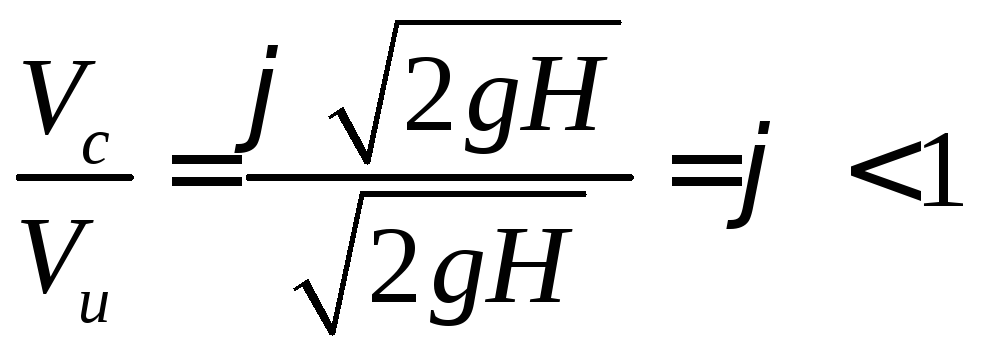, (8.5)

Коэффициент φ равен отношению скорости истечения реальной жидкости к скорости истечения идеальной жидкости.Коэффициент φ < 1 из-за наличия вязкости у реальной жидкости.

Умножив площадь сечения сжатой струиSc = εSона скорость струи в сжатом сечении, получим выражение для расхода жидкости через отверстие с острой кромкой при совершенном сжатии

(8.6)

Коэффициентом расхода при истечении из отверстия μ называется произведение коэффициента сжатия ε на коэффициент скорости φ

μ = ε * φ. (8.7)

Расхода через отверстие с острой кромкой при совершенном сжатии

(8.8) или(8.9)

где Н- напор истечения или расчетный напор, а ΔР=(р1-Р2)/ρg— расчетная разность давлений, под действием которой происходит истечение.

По этим формулам определяется расход истечения из отверстия с острой кромкой и через насадки различных форм.

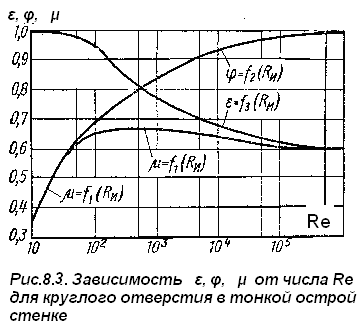
На рис. 8.4 показаны составленные А.Д. Альтшулем зависимости для коэффициентов ε, φ иμ для круглого отверстия в функции числаRе.

1.Увеличение числа означает уменьшение сил вязкости, влияние трения становится меньше, поэтому коэффициент сопротивленияζ уменьшается, и коэффициент скоростивозрастает.

2. Коэффициент εуменьшается из-за уменьшения торможения жидкости у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую часть. ПриRе→∞значения коэффициентов приближаются кφ→1 иε→0,6.

3 Коэффициент расхода равный произведению μ = ε * φс увеличениемReсначала растет, что связано с ростомφ, а затем уменьшается в связи со значительным падениемε, при большихRе_иравенμ= 0,60÷0,62.

4. В области малых Re(Rе_и< 25) роль вязкости велика, торможение жидкости у кромки значительно, сжатие струи почти отсутствует иε = 1, φ = μ.

При числах Re<23 для определенияμможно пользоваться формулой:

(8.11)

5.При увеличении скорости и числах Рейнольдса Re> 10⁵ , Re почти не влияет на ко­эффициенты истечения (квадратичная зона истечения), для рас­четов можно пользоваться средними значениями: φ = 0,97; ε= 0,62; μ = 0,60.

При турбулентном режиме движения неравномерность средних скоростей в сжатом сечении струи невелика, α_т = 1, при φ = 0,97 можно принимать в среднем для круглого отверстия с острой кромкой при несовершенном сжатии

(8.12)

6.Коэффициент полезного действия отверстия - отношение удельной кинетической энергии струи к напору истечения:

где (8.13)

7. При больших Re α=1, КПД равен (8.14)

8. Для малых отверстий некруглой формы при больших Re значения коэффициента расхода в формуле для определения расхода можно принимать равны­ми μ= 0,6.