4.4.1 Ограничивающий прямоугольник

Теперь рассмотрим функцию Arc, которая рисует эллиптическую кривую. Рассмотрение функции Arc не имеет смысла без предварительного рассмотрения функции Ellipse, рассмотрение функции Ellipse не имеет смысла без рассмотрения функции Rectangle. Если рассматривать функции Ellipse и Rectangle, то следует разобраться также с функциями RoundRect, Chord и Pie.

Проблема в том, что функции Rectangle, Ellipse, RoundRect, Chord и Pie предназначены не только для рисования линий. Да, эти функции рисуют линии, но они также закрашивают ограниченную этими линиями область, используя текущую кисть. По умолчанию эта кисть сплошная и белая, поэтому, начиная экспериментировать с этими функциями, вы могли не заметить, что они делают еще что-то, кроме рисования линий. Строго говоря, эти функции относятся к следующему разделу "Рисование закрашенных областей", но, тем не менее, рассмотрим их здесь.

Все функции, которые были указаны выше, схожи в том, что все они строятся с использованием "ограничивающего прямоугольника" (bounding box). Вы определяете координаты прямоугольника, ограничивающего объект, и Windows рисует объект, используя этот прямоугольник.

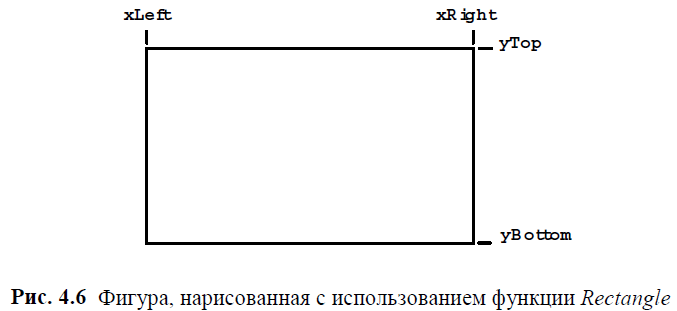
Простейшей из этих функций является функция рисования прямоугольника:

Rectangle(hdc, xLeft, yTop, xRight, yBottom);

Точка с координатами (xLeft, yTop) — это левый верхний угол прямоугольника, а точка (xRight, yBottom) — правый нижний угол. Фигура, нарисованная с использованием функции Rectangle, приведена на рис. 4.6. Стороны прямоугольника всегда параллельны горизонтальной и вертикальной сторонам экрана.

Программисты, ранее работавшие с графикой, привыкли к проблеме одного пикселя. Некоторые графические системы изображают фигуры, включающие правую и нижнюю координаты, а некоторые — рисуют фигуры до правой и нижней координаты, не включая их.

Windows использует последний подход. Есть простой путь для иллюстрации сказанного. Предположим, вызывается функция:

Rectangle(hdc, 1, 1, 5, 4);

Как уже говорилось, Windows использует для рисования ограничивающий прямоугольник. Вы можете представить себе дисплей как сетку, каждая ячейка которой представляет один пиксель. Воображаемый ограничивающий прямоугольник рисуется по сетке, а выводимый прямоугольник рисуется с использованием ограничивающего. Это выглядит так:

Ширина полос, отделяющих прямоугольник от верхней и левой границ рабочей области окна равна 1 пикселю. Windows использует текущую кисть для зарисовки 2-х пикселей внутри прямоугольника. Вы уже знаете, как нарисовать прямоугольник, теперь надо выяснить, как нарисовать эллипс, поскольку для этого необходимы те же параметры:

Ellipse(hdc, xLeft, yTop, xRight, yBottom);

Фигура, отображаемая функцией Ellipse (вместе с ограничивающим прямоугольником) приведена на рис. 4.7.

Функция для рисования прямоугольника со скругленными углами применяет тот же ограничивающий прямоугольник, что и функции Rectangle и Ellipse, но с двумя дополнительными параметрами:

RoundRect(hdc, xLeft, yTop, xRight, yBottom, xCornerEllipse, yCornerEllipse);

Фигура, отображаемая этой функцией приведена на рис. 4.8.

Windows использует маленький эллипс для рисования скругленных углов. Ширина этого эллипса равна xCornerEllipse, а высота равна yCornerEllipse. Представьте себе, что Windows делит этот маленький эллипс на четыре квадранта по одному на каждый из четырех углов. Округлость углов более заметна при больших значениях xCornerEllipse и yCornerEllipse. Если значение xCornerEllipse равно разности между xLeft и xRight, а yCornerEllipse — разности между yTop и yBottom, то функция RoundRect будет отображать эллипс. Скругленные углы, показанные на рис. 4.8, были нарисованы с использованием размеров углового эллипса, вычисленных по формулам:

xCornerEllipse =(xRight — xLeft) / 4;

yCornerEllipse =(yBottom — yTop) / 4;

Это простое приближение, но результаты, скорее всего, будут выглядеть не совсем правильно, потому что округлость углов более заметна при больших размерах прямоугольника. Для решения этой проблемы, вы, вероятно, захотите сделать равными реальные размеры xCornerEllipse и yCornerEllipse.

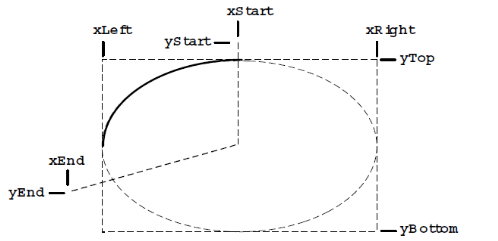
В функции Arc, Chord и Pie передаются одинаковые параметры:

Arc(hdc, xLeft, yTop, xRight, yBottom, xStart, yStart, xEnd, yEnd);

Chord(hdc, xLeft, yTop, xRight, yBottom, xStart, yStart, xEnd, yEnd);

Pie(hdc, xLeft, yTop, xRight, yBottom, xStart, yStart, xEnd, yEnd);

Линия, рисуемая функцией Arc приведена на рис. 4.9; фигуры, отображаемые функциями Chord и Pie, приведены на рис. 4.10 и 4.11. Windows использует воображаемую линию для соединения точки (xStart, yStart) с центром эллипса. В точке, где эта линия пересекается с ограничивающим прямоугольником, Windows начинает рисовать дугу эллипса в направлении против часовой стрелки. Windows также использует воображаемую линию для соединения точки (xEnd, yEnd) с центром эллипса. В точке, где эта линия пересекается с ограничивающим прямоугольником, Windows завершает рисование дуги.

В случае функции Arc действия Windows на этом заканчиваются, поскольку дуга — эллиптическая кривая, не ограничивающая замкнутую область. В случае функции Chord Windows соединяет конечные точки дуги. В случае функции Pie Windows соединяет начальную и конечную точки дуги с центром эллипса. Внутренняя область фигур, образуемых функциями Chord и Pie, закрашивается текущей кистью.

Вас может удивить использование начальной и конечной позиций в функциях Arc, Chord и Pie. Почему бы просто не указать начальную и конечную точки на кривой эллипса? Хорошо, вы можете сделать так, но вам придется численно описать, что это за точки. Метод, применяемый в Windows, работает, не требуя этих уточнений.

Программа LINEDEMO рисует прямоугольник, эллипс, прямоугольник с скругленными углами и два отрезка, но в другом порядке. Эта программа показывает, что функции, определяющие области, закрашивают их. Поэтому отрезки не видны там, где нарисован эллипс.

См. Лабораторная работа 4.