2. Механика

   1. Движение материальной точки

      1. Кинематика материальной точки

В кинематике движение тел рассматривают формально, без объяснения причин и характера изменения движения и, следовательно, не используют ни понятие силы , ни понятие массы т тела.

Простейшей физической системой является либо одна материальная точка, либо их относительно небольшая совокупность.

Положение материальной точки относительно какой-либо системы отсчета в произвольный момент времени t определяется радиус-вектором (рис.2.1). Если ввести единичные векторы (орты) , направленные по соответствующим осям (OX, OY, OZ), то радиус-вектор можно представить в таком виде:

, (2.1)

где x(t), y(t), z(t) – компоненты радиус-вектора .

Одновременное задание трех функций x(t), y(t) и z(t) эквивалентно заданию одной векторной функции от скалярного аргумента t. Уравнение (2.1) называют законом движения материальной точки. Таким образом, закон движения (2.1) определяет положение материальной точки в любой момент времени.

Вектор скорости и вектор ускорения определяются через соответствующие производные:

, (2.2)

. (2.3)

Закон движения (2.1) является фундаментальным в кинематике. Зная закон движения, можно определить другие физические величины, характеризующие движение материальной точки, например компоненты вектора скорости , ускорения и т.д.:

; (2.4)

. (2.5)

Следовательно, с законом движения (2.1) связана основная задача кинематики. Формально этих задач две: прямая и обратная. Прямая основная задача кинематики заключается в нахождении любого параметра движения по известному закону движения. Она решается путем последовательного применения основных законов кинематики (2.1) – (2.3). Обратная задача кинематики состоит в определении закона движения по какому-либо известному параметру движения (вектора скорости или ускорения ). Обратная задача значительно труднее прямой. Рассмотрим примеры прямой и обратной задач кинематики.

1. Определить модуль скорости материальной точки в момент времени t=2 c, если точка движется по закону 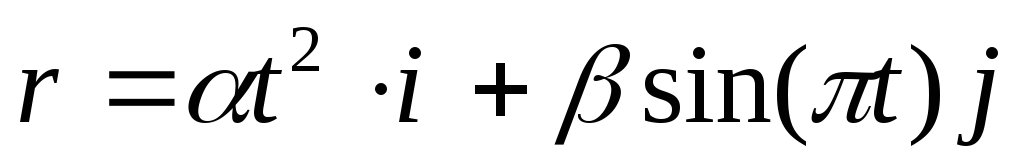, где 2 м/с², 3 м.

Решение. Физический анализ⁴. Физическая система состоит из одного идеального объекта – материальной точки. Задан формально закон ее движения. Следовательно, наша задача – прямая задача кинематики (по известному закону движения определить один из параметров движения – в данном случае модуль вектора скорости). Используя известный закон движения, находим, что компоненты радиус-вектора

, (2.6)

, (2.7)

. (2.8)

Таким образом, материальная точка движется в плоскости XOY, поэтому каждый из векторов , и имеет две компоненты. По определению вектора скорости из уравнений (2.2), (2.4), (2.6) и (2.7) получаем компоненты вектора скорости:

.

Отсюда находим искомый модуль вектора скорости:

.

Подставив численные значения, получим v12,4 м/с.

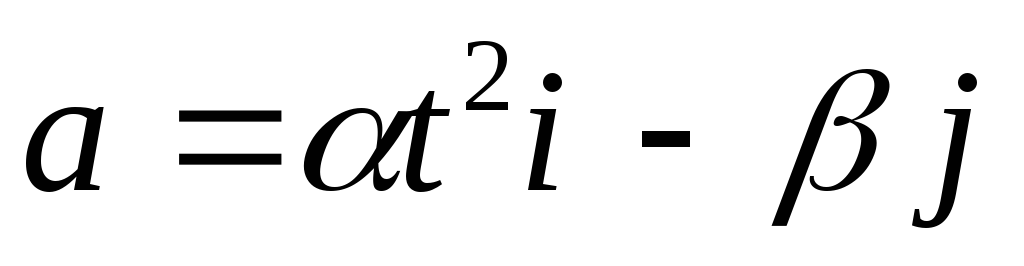2. Ускорение материальной точки изменяется по закону , где 3 м/с⁴, 3 м/с². Найти, на каком расстоянии от начала координат она будет в момент времени t=1 с, если и при t=0.

Решение. Из условия задачи видно, что материальная точка движется в плоскости XOY. Для того, чтобы определить, на каком расстоянии от начала координат она находилась в момент времени t=1 с, необходимо знать закон ее движения. Таким образом, перед нами обратная задача кинематики: дан какой-то параметр движения (в данном случае ускорение ), надо определить закон движения и далее найти модуль радиус-вектора в момент времени t=1 с.

Сначала определим вектор скорости из уравнения (2.3):

или .

Это векторное дифференциальное уравнение эквивалентно двум дифференциальным уравнениям:

.

Разделяя переменные и интегрируя, получим компоненты вектора скорости:

.

Учитывая начальные условия ( при t=0) находим значения произвольных постоянных с₁=0 и с₂=0.

Далее из системы дифференциальных уравнений

определяем компоненты x(t) и у(t) радиус-вектора :

, (2.9)

где с₃ и с₄ – произвольные постоянные.

Учитывая начальные условия (х=0, у=0 при t=0), из уравнений (2.9) находим, что с₃=с₄=0. Закон движения найден:

. (2.10)

По формуле для модуля радиус-вектора определяем искомое расстояние материальной точки от начала координат в момент времени t=1 с:

1,52 м.

Анализ решения. Зная закон движения, можно найти любой параметр, характеризующий движение материальной точки, и, следовательно, поставить и решить множество других кинематических задач. Сформулируем, например, задачу о нахождении траектории данной материальной точки: по заданному ускорению и тем же начальным условиям (их можно изменить) определить траекторию материальной точки. После того как будет получен закон движения (2.10), траектория определиться из системы уравнений

.

Исключив из этой системы время t, можно найти уравнение траектории.

Совокупность методов решения прямой и обратной задач кинематики составляет сущность кинематического метода, о котором упоминалось в подразделе 1.2.3.