§ 5. «Парадоксы бесконечного» б. Больцано

Кроме, собственно, Лейбница в истории европейской философии у Кантора было мало авторитетных союзников, однозначно поддерживавших тезис о существовании актуальной бесконечности в тварном мире и постижимости ее человеческим разумом. Тем дороже была для создателя теории множеств позиция Бернарда Больцано (1781–1848), чешского философа и математика, также пытавшегося построить некоторое исчисление бесконечностей. Кантор невысоко оценивал позитивно-научный вклад Больцано в учение о бесконечном, однако философские позиции последнего были чрезвычайно симпатичны автору теории множеств. «Ре­ши­тельного защитника собственно бесконечное, —писал Кантор,—...нашло в одном в высшей степени остроумном философе и математике нашего столетия, в Бернарде Больцано, который развил свои взгляды на этот вопрос в прекрасном и содержательном сочинении «Pa­radoxien des Unendlichen»¹, Leipzig, 1851, имеющем целью показать, как противоречия, отыскивавшиеся в бесконечном скептиками и перипатетикамивсех времен, вовсе не оказываются в нем, лишь только берут на себя, правда, не совсем легкий труд рассматривать понятия о бесконечности со всей серьезностью в их истинном значении»¹. Действительно, в начале своей небольшой книжечки «Парадоксы бесконечного» Больцано объявляет о ее главной цели: показать, что так называемые парадоксы, связанные с понятием бесконечности, являются лишь «кажущимися противоречиями». В книге рассматриваются некоторые общефилософские вопросы, касающиеся бесконечного, математическое применение этого понятия, а также роль бесконечности в рамках того варианта спекулятивного атомизма, который развивал сам Больцано. Для нашей книги важны именно две первые темы.

Из всех представлений о бесконечном главным является, по Больцано, именно количественноепонимание бесконечного. Даже когда мы говорим о бесконечности Бога, мы имеем в виду, «что Он владеет силами более чем одного рода, имеющими бесконечную величину»². Но количеством (и величиной) занимается имен­но математика. Поэтому именно математические конструкции с бесконечностью имеют принципиальное значение. Интересно, что Больцано дает определениемножества, в целом тождественное с канторовским употреблением этого термина: «Совокупность, определяемую таким понятием, при котором расположение частей безразлично (в которой, следовательно, не происходит никаких существенных изменений, если меняется только расположение частей),—такую совокупность я называюмногообразием; а такое многообразие, все части которого будут рассматриваться какединицыизвестного рода А, т.е. как предметы, содержащиеся в понятии А, называетсямножествомпредметов А»¹. Однако Больцано не строит на этом основании никакой новойтеориимножеств. Он, как мы увидим, пытался получить исчисление бесконечностей другим путем.

Бесконечное количество определяется Больцано следующим образом: «Я буду называть бесконечным количеством количество большее, чем каждое конечное, т.е. количество такого рода, что каждое конечное многообразие представляет только часть его»². В этом определении были важны два момента. С одной стороны, говоря о бесконечном как о бесконечномколичестве, Больцано тем самым полагает, что речь идет обактуально данномколичестве. Поэтому потенциальная бесконечность сразу исключается из рассмотрения как лишь некий несобственный модус бесконечного. С другой стороны, предложенное определение достаточно широко, чтобы не сводиться к слишком частному, по мнению Больцано, пониманию бесконечного у Спинозы: бесконечно то, что неспособно к дальнейшему увеличению. Для чешского математика существуют различные градации бесконечного. Впрочем, понимание их не имеет ничего общего с будущими конструкциями Кантора: если к точкам отрезка добавить одну точку, то, по Больцано, получится большее множество точек, и, уж конечно, количество точек плоскости больше, чем точек прямой³.

Обладает ли понятие бесконечности предметным смыслом, т.е. существуют ли действительно актуально бесконечные множества? Больцано решительно настаивает на положительном ответе. Прежде всего, актуально бесконечное существует в мысли. «Мно­го­образие предложений и истин самих в себе — бесконечно», — утверждает философ. Доказательство этого тезиса выглядит так: частью многообразия истин самих в себе является множество, которое строится следующим образом: берем какую-нибудь истину А, например, что истины вообще существуют, затем строим новое предложение — «А — истинно» — и обозначаем его через В. Аналогично строим предложение «В — истинно», обозначаем его через С и так далее, до бесконечности. Все полученные истинные предложения различны (они имеют различные подлежащие), и их бесконечное количество. Поэтому и многообразие истин в себе также бесконечно.

Больцано отрицает правомочность возражения, что так построенное многообразие истин мы не можем представитьцеликом, т.е. имея, так сказать, «наличным» представление о каждом отдельном члене этого ряда. Точно таким же образом, подчеркивает он, мы не можем представить себе население Праги или Пекина (т.е. располагая точным знанием о каждом жителе), и тем не менее мы считаем, что имеет смысл говорить о количестве жителей этих городов. Вообще, утверждал Больцано, мы можем рассматривать любую совокупность предметов, обладающих некоторым родовым признаком А, безразлично, конечна или бесконечна эта совокупность. Тем самым в свете открывшихся в дальнейшем парадоксов теории множеств (парадокс Рассела, «множество всех множеств» и т.д.) настойчивость Больцано в этом пункте была не слишком глубокомысленной...

Что же касается, так сказать, «онтологического доказательства» существования актуальной бесконечности, то оно у Больцано опирается на тезис, что бесконечно могущественный Бог должен был де сотворить актуально бесконечное и в мире. Этот же постулат будет использовать потом и Кантор ¹ в своем «онто­ло­ги­чес­ком доказательстве», однако отнюдь не обязательно, что создатель теории множеств воспринял это навязчиво соблазнительное соображение непосредственно от Больцано ². Бог у Больцано «беско­неч­но много знает (совокупность всех истин), бесконечно много желает (сумму всего в себе возможного добра) и все, чего только хочет, силою внешнего воздействия осуществляет в действительности»¹. С первым и последним можно, безусловно, согласиться, однако почему Бог обязательно бесконечно много желает — непонятно. И ссылка на «все возможное в себе добро» мало что здесь проясняет... Но, если все-таки принять эти больцановские постулаты, то тогда действительно становится более или менее правдоподобным, что «бес­ко­неч­но много желающий Бог» создает бесконечное многообразие существ... Мы думаем, что традиционное христианское богословие понимало этуактуально бесконечную явленностьБога в мире, скорее, совсем в ином смысле. Но об этом будет сказано ниже, когда мы будем говорить о теологических взглядах самого Кантора².

Свое исчисление бесконечностиБольцано понимает в особом смысле. Речь идет не о «вычислении бесконечности», так как бесконечность неопределима никаким числом, а об определенииотношения«одной бесконечности к другой», что, по Больцано, иногда возможно эффективно осуществить. Что здесь имеется в виду—лучше обсудить на примерах. Больцано рассматривает сумму ряда натуральных чисел:

1 + 2 + 3+ 4 +...+ n+ (n+ 1) + ... in inf.,³,

затем вводит символ :

1⁰+ 2⁰+ 3⁰+ 4⁰+...+n⁰+ (n+ 1)⁰+ ... in inf. =. (1)

Нулевые степени натуральных чисел все равны единице, так что , собственно, равно сумме

1 + 1 + 1 + 1 + ... до бесконечности.

Потом вводится символ :

(n+ 1)⁰+ (n+ 2)⁰+ (n+ 3)⁰+ ... in inf. =. (2)

После из равенства (1) вычитается равенство (2) (левые и правые части соответственно) и получается

1⁰+ 2⁰+ 3⁰+ ...n⁰=n=—. (3)

Причем Больцано подчеркивает, что равенства (1) и (2) суть «чис­­то символические равенства», а равенство (3) уже «со­вер­шен­но безупречноеравенство, из которого мы видим, как иногда две бесконечные величиныиимеют совершенно определенную конечную разность»¹[выделено мной.—В.К.] Однако логика этого вывода «хромает», и «бе­зуп­реч­ность» равенства (3) довльно сомнительна. Ведь если (1) и (2)—просто символические равенства, так как никто не знает, как можно суммировать бесконечные ряды слева, то отнюдь не очевидно, что эти бесконечные ряды можно как-то «вычитать» один из другого, например так, как это делает сам автор. Как, впрочем, и непонятно, как можно вычитать символ одной бесконечности из другого...

Применяя подобную же, не обоснованную в случае бесконечных сумм технику, Больцано аналогично получает (ум­но­жая обе части на ):

1⁰× + 2⁰× + 3⁰×+ ... in inf. = ()²,

1⁰×()²+ 2⁰×()²+ 3⁰×()²+ ... in inf. = ()³и т.д.

«Из этого мы видим, —заключает автор,—что существуют бесконечные величины так называемыхвысших порядков, из которых одна превосходит другую в бесконечное число раз. Существование бесконечных величин, имеющих рациональное, так же как и иррациональное отношениеa:b, вытекает уже из того, что, посколькуозначает неизменную бесконечную величину, постолькуa×иb×представляют пару бесконечных величин, находящихся в отношенииa:b»¹.

Бесконечное количество точек на отрезке Больцано хочет связать с длиной этого отрезка: «Не менее ясным окажется и то, что все многообразие(множество) величин, находящихся между двумя данными величинами, например между 7 и 8, хотя оно ибесконечнои не может быть вследствие этого определено никаким числом, как бы велико последнее ни было, зависит, однако, единственно от величины расстояния этих двух крайних величин, т.е. зависит от величины 8—7, и должно быть вследствие этого одинаковым, как только это расстояние одинаково. В этом предположении, если обозначить количество всех величин, лежащих между a и b через Mult. (b—a), то получаются бесчисленные равенства следующего вида:

Mult. (8—7) = Mult. (13—12),

а также и следующего:

Mult. (b—a) : Mult. (d—c) = (b—a) : (d—c),

против правильности которых нельзя возразить ничего основательного»². Требуя логической «презумпции невиновности» для своих утверждений, Больцано как бы забывает о необходимости «пре­зумпции их доказанности»: еслипротивэтих утверждений нельзя возразить «ничего основательного», то в то же время иза нихнельзя привести достаточно убедительных доводов...

Анализируя эти и другие примеры построения этого своеобразного «исчисления бесконечности» у Больцано, нетрудно догадаться, на какую методологическую парадигму он здесь ориентируется. Больцано хочет получить соотношения для бесконечных множеств, используя их «участие» в уже известных математических конструкциях и опираясь на известные свойства и формулы последних. Такой прием в математике называется методом идеальных элементов ¹.Именно таким способом, например, исторически утвердилось в математике комплексное число. Никто не знал, что такое. Более того, было понятно, что такого действительного числа не существует. Однако для нужд вычислений с действительными числами оказалосьполезнымвведение этого символаi=, про который по определению можно было сказать только, чтоi² =-1. Но этот чисто условный символ, «идеальный элемент», позволил значительно расширить границы теории функции, найти новые методы решения старых классических задач, найти новые, более общие подходы. Больцано был прекрасно осведомлен обо всем этом. И он пытается ввестибесконечностькак такой новый идеальный элемент (например, символ Mult. (a—b)), ввести его каким-нибудь образом в уже известные теории и формулы и получить на этот элемент новые соотношения. Другими словами, он стремится как бычисто техническиовладеть бесконечностью, без встречи с ней, так сказать, непосредственно, «лицом к лицу», без прямого обсуждения ее свойств...

Хотя Больцано и утверждал, что количество точек на отрезках разной длины различно (Mult. (b—a) : Mult. (d—c) = (b—a) : (d—c)) и что будто бы против этого «нельзя возразить ничего основательного», однако на самом деле эти возражения были уже давно известны. Не были они новостью и для самого Больцано. Речь идет о взаимно однозначном соответствии между точками любых отрезков:

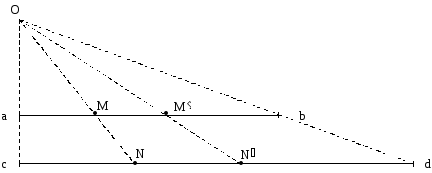
Рис. 1

С помощью такой, например, проективной конструкции можно любой точке М отрезка [a;b] поставить в соответствие точку N отрезка [c;d] так, что соответствие будет взаимно однозначным и лишних точек не останется. Этот прием —классический пример парадоксальных свойств бесконечных множеств: количество точек на отрезках разной длины одинаково. Однако особенность позиции Больцано в том и состояла, что онне хотел соглашаться с этим выводом. Впрочем, он не может привести каких-то решающих доводов и против всей фундаментальной очевидности взаимно однозначного соответствия точек двух отрезков. Больцано лишь многословно объясняет, что для равенства двух многообразий (как множеств) они должны быть равны «во всех отношениях» (т.е., по существу, тождественны, что, собственно, достаточно банально). И по этой логике поскольку, например, в нашем проективном соответствии NN' > MM', то «отсюда естественно следует, что в промежутке каждых двух величин в B содержится другое (боль­шее [???—В.К.]) количество величин, чем это имеет место в A; таким образом, нет ничего удивительного, что и все количество величин в B другое (больше), чем в A»¹. Другими словами, по Больцано, количество точек в большем отрезке больше.

Аналогично «длина прямой, простирающейся безгранично в направлении аR, бесконечна, но... прямая bR,

S b а R

Рис. 2

из точки b идущая в том же направлении, больше, чем aR, на отрезок ba... и прямая, идущая неограниченно в обоих направлениях aR и aS, должна быть названа большей на величину, которая сама бесконечна...»¹. Не хочет Больцано признавать взаимно-однозначного соответствия и в аналитических выражениях. Поэтому в сумме

1 + е + e²+ ... + eⁿ+ eⁿ⁺¹+ ... in inf.

членов на n больше, чем в сумме

eⁿ+ eⁿ⁺¹+ ... in inf.,

несмотря на то, что вторая сумма, по признанию самого же Больцано, равна

eⁿ(1 + е + e²+ ... + eⁿ+ eⁿ⁺¹+ ... in inf.)².

Больцано хочет уйти от парадоксов, сохранив, так сказать, наивнуюточку зрения. Эта деланная наивность, однако, дается не без некоторого труда, как показывает последний пример. Таким же духом соединения тщательности и бесплодности отмечены попытки ввести «единицы бесконечности» разных размерностей. Так, если количество точек, лежащих на единичном отрезке (вместе с концами), мы обозначим через Е, то количество точек на отрезке длины n будет

nE—(n—1),

так как nединичных отрезков будут пересекаться в (n—1) точке. Аналогично, если количество точек в квадрате со стороной 1, включая и точки на границе, мы обозначим через E², то количество точек в прямоугольнике со сторонами m и n будет

mnE²—[n(m—1) +m(n—1) ] E + (m—1) (n—1).

Аналогичные формулы пишутся и для параллелепипеда.

На фоне этих достаточно бесплодных вычислений еще ярче выступает интеллектуальная дерзость Кантора, принявшего все известные парадоксы бесконечности как ее характерные свойства и начавшего последовательно строить на этих необычных основаниях новую теорию. Больцано пытается, так сказать, «косвенно» овладеть бесконечностью, через метод идеальных элементов. Поэтому ему нужно связать вводимые символы бесконечности (E, E², Mult. (b— a) и т.д.) с метрическими¹свойствами фигур. Однако попытка не удается. Существенно новых свойств из чисто технического оперирования с символами бесконечности не получается. Нет новой идеи. Кантор же прямо кладет в основание своей теории в качестве определения равенства мощностей множеств процедуру взаимно однозначного соответствия элементов множеств. Правда, тем самым разрываются связи теоретико-множественных построений не только с метрическими свойствами фигур, но даже и с топологическими. Отрезок и куб любой размерности оказываются как множества точек равномощными, однако взаимно од­но­знач­ное соответствие между ними осуществляется функцией разрывной и в высшей степени искусственной... Но это не останавливает Кантора, и он последовательно идет по выбранному пути.

Больцановская попытка, так сказать, «с бокового входа» войти в сферу бесконечного не удалась. При всей симпатии к философским установкам Больцано в отношении бесконечного Кантор ясно осознавал стерильность больцановских построений для «ариф­метики бесконечного». «Больцано, быть может, единственный автор, —писал Кантор,—который до некоторой степени оперирует собственно бесконечными числами; по крайней мере у него о них неоднократно идет речь. Однако я никак не могу согласиться с тем способом, каким он трактует их, не будучи в состоянии дать им правильное определение, и, например, § 29–33 его книги я считаю необоснованными и ошибочными. Для действительного выражения в понятиях определенно бесконечных чисел у этого автора не хватает как общегопонятия мощности, так и точногопонятия количества. Правда, в отдельных местах оба последние встречаются у него в зародышевом виде в форме специализаций, но, как мне кажется, при этом он не может достигнуть полной ясности и определенности, чем и объясняются многие непоследовательности и даже ошибки этой замечательной книги.Безвышеупомянутых двух понятий невозможно, по моему мнению, продвинуться вперед в учении о многообразиях»¹.

В обсуждаемой работе Больцано попытался также дать и свою конструкциюконтинуума. Как и Кантор, автор «Пара­док­сов» был убежден, что континуум можно (и должно) построить из точек: «Следует настаивать на том, что каждый континуум не может произойти в конце концов ни из чего другого, кроме точек, и только точек»². Больцано предложил, однако, неправильную конструкцию континуума: «Континуум существует там, и только там, где имеется совокупность простых предметов (точек во времени или в пространстве, или субстанций), расположенных таким образом, что каждый из них на каждом, сколь угодно малом расстоянии имеет, по крайней мере, один соседний с ним предмет»³. Подобным свойством обладает, например, множество рациональных чисел отрезка [0; 1], которое, однако, не исчерпывает всего континуума [0; 1], так как в нем имеются и иррациональные числа. Кантор, предлагая свою модель континуума как «совершенного и связного множества», отметил также и несостоятельность больцановской конструкции⁴.

В целом, заключая этот параграф, можно констатировать: несмотря на общность философских интенций Кантора и Больцано, последнему не удалось построить какие-то новые положительно-научные математические конструкции, оперирующие с актуально бесконечным. В бесконечное Больцано надеялся войти «по непрерывности», используя соотношения бесконечного с конечным, опираясь на логическую непрерывностьсвойств финитных и бесконечных объектов, в духе метода «идеальных элементов». То же, что суждено было предложить в скором будущем Кантору, представляло собой именно нарушение логической непрерывности—скачокв трансфинитное.