
- •Введение
- •Глава 2. Параллактический треугольник светила и его решение
- •§4. Параллактический треугольник и его решение по основным формулам
- •§5. Вычисление высоты и азимута светила по системам формул
- •§7. Разложение высоты и азимута в ряд Тейлора. Теория таблиц численного типа
- •§1. Небесная сфера
- •§2. Системы сферических координат
- •§3. Графическое решение задач на небесной сфере
- •Глава 3. Видимое суточное движение светил. Изменение координат светил
- •§9. Характеристика суточного движения светил
- •§10. Явления, связанные с суточным движением светил
- •§11. Изменение координат светил вследствие видимого суточного движения
- •Глава 4. Обращение Земли вокруг Солнца. Видимое движение Солнца и изменение его координат
- •§13. Обращение Земли по орбите и видимое годовое движение Солнца
- •§14. Изменение экваториальных координат Солнца в течение года
- •Глава 5. Орбитальное и видимое движение планет, Луны и искусственных спутников
- •§18. Фазы и возраст Луны
- •§21. Орбитальное движение искусственных спутников
- •Глава 6. Измерение времени
- •§22. Основы измерения времени
- •§23. Звездные сутки. Звездное время. Основная формула времени
- •§26. Поясное, декретное, летнее, московское и стандартное времена, их связь с местной системой
- •§28. Понятие о точных шкалах времени
- •Глава 7. Вычисление видимых координат светил. МАЕ
- •§31. Понятие о вычислении видимых координат светил на ЭВМ
- •§32. Устройство таблиц МАЕ для расчета часовых углов и склонений светил
- •§33. Определение времени кульминации светил
- •§34. Обоснование расчета времени видимого восхода (захода) Солнца и Луны и времени сумерек
- •§35. Определение времени восхода и захода Солнца и Луны и времени сумерек по МАЕ
- •Глава 8. Измерители времени. Судовая служба времени
- •Глава 9. Звездное небо. Звездный глобус
- •§42. Устройство звездного глобуса, его установка. Понятие о других пособиях
- •§43. Решение задач с помощью звездного глобуса
- •Глава 10. Секстан
- •§44. Основы теории навигационного секстана
- •§45. Устройство навигационных секстанов
- •§46. Понятие об инструментальных ошибках секстана и их учете
- •§47. Понятие о секстанах с искусственным горизонтом
- •Глава 11. Наблюдения с навигационным секстаном
- •§48. Выверка навигационного секстана на судне
- •§50. Приемы измерения высот светил над видимым горизонтом
- •§53. Наклонение видимого горизонта. Наклонение зрительного луча
- •§55. Общий случай исправления высот светил, измеренных над видимым горизонтом
- •§56. Частные случаи исправления высот светил
- •§57. Приведение высот светил к одному зениту (месту) и одному моменту
- •§58. Определение средних квадратических ошибок поправок и измерения углов
- •§59. Определение средней квадратической ошибки измерения высот светил в море
- •Глава 13. Астрономическое определение поправки компаса
- •§60. Основы астрономического определения поправки компаса
- •§62. Пеленгование светил. Точность поправки компаса
- •§63. Определение поправки компаса. Общий случай
- •Глава 14. Теоретические основы определения места судна по светилам
- •§65. Общие принципы астрономического определения места
- •§67. Метод линий положения. Высотная линия положения
- •§72. Ошибки в высотной линии. Оценка ее точности и вес
- •Глава 16. Методы отыскания места судна и оценки его точности при наличии ошибок в высотных линиях
- •Глава 17. Определение места по одновременным наблюдениям светил. Общий случай
- •§76. Особенности определения места по одновременным наблюдениям светил
- •§77. Общий случай определения места по звездам
- •§78. Определение места днем по одновременным наблюдениям Луны и Солнца
- •§79. Определение места днем по одновременным наблюдениям Венеры и Солнца
- •§80. Определение места по одновременным наблюдениям Венеры, Луны и Солнца
- •Глава 18. Определение места судна по разновременным наблюдениям Солнца
- •§81. Особенности определения места по разновременным наблюдениям Солнца
- •§82. Влияние ошибок счисления и наивыгоднейшие условия для определения места по Солнцу
- •§83. Определение места по Солнцу в общем случае
- •§84. Определение места комбинированием навигационных и астрономических линий положения
- •Глава 19. Ускоренные способы обработки наблюдений
- •§86. Обзор приемов ускорения обработки наблюдений
- •§87. Прием перемещения счислимого места
- •§88. Определение места с предварительной обработкой (предвычислением) линий положения
- •§92. Решение астрономических задач на клавишных ЭВМ
- •Глава 20. Частные методы определения координат места судна
- •§93. Определение широты места по меридиональной и наибольшей высотам Солнца. Понятие о близмеридиональных высотах
- •§96. Определение координат места в малых широтах по соответствующим высотам Солнца
- •§97. Графический способ определения места при высотах Солнца, больших 88°
- •§98. Особенности определения места в высоких широтах
- •Глава 21. Перспективы развития методов астрономических определений в море. Краткий исторический очерк
- •§99. Понятие об астронавигационных системах и навигационных комплексах
- •§100. Краткий очерк истории мореходной астрономии
- •Список литературы
Глава 16
МЕТОДЫ ОТЫСКАНИЯ МЕСТА СУДНА И ОЦЕНКИ ЕГО ТОЧНОСТИ ПРИ НАЛИЧИИ ОШИБОК В ВЫСОТНЫХ ЛИНИЯХ
§73. ОТЫСКАНИЕ ВЕРОЯТНЕЙШЕГО МЕСТА СУДНА ПРИ НАЛИЧИИ В ВЛП ТОЛЬКО СЛУЧАЙНЫХ ОШИБОК. ОЦЕНКА ЕГО
ТОЧНОСТИ
При отсутствии ошибок уравнение ВЛП имеет вид
∆φ cos A+∆W sin A=n
где n – истинный перенос относительно счислимого места Мс. Очевидно, что для определения неизвестных ∆φ и ∆W достаточно
получить два таких уравнения, т.е. две линии, и, решая их совместно, определить действительные φ и λ, или в графическом варианте – действительное место судна. В реальных условиях в линиях положения или переносе n всегда есть ошибки, поэтому двух линий заведомо недостаточно для получения надежного места. Рассмотрим действие ошибок и методы обработки (уравнивания) сначала раздельно для случайных и систематических ошибок, а в §75 совместно.
Уравнение ВЛП со случайной ошибкой и полоса положения. Полагая, что наблюдения и обработка выполнены правильно, т.е. что промахов нет и систематические ошибки исключены, в переносе остается только индивидуальное значение случайной ошибки v и уравнение (227) примет вид
∆φ cos A+∆W sin A=n+v (242)
Так как в каждой высотной линии своя ошибка ui, то число неизвестных в уравнениях (242), т.е. ∆φ, ∆W и vi, всегда оказывается большим числа уравнений и все значения vi не определяются. Однако, хотя каждая ошибка ui неизвестна, из опытов устанавливается возможное рассеивание ее значений (дисперсия) и средняя квадратическая ошибка m (ее значения для ВЛП
348
показаны в §72). Метод учета и заключается в «накрытии» ее величиной ±mn, т.е. в том, что в уравнение (242) вместо u вводится значение mn и получается уравнение полосы положения, в пределах которой с вероятностью 68% должна находиться действительная линия. Следовательно, построив полосу с границами ±mn, мы как бы «накрываем» действительную линию, хотя указать точно ее положение не можем.
Площадь положения, оценка точности и вес места. Для нескольких линий уравнения полос положения (240) запишем в виде
∆φ cos Ai+∆W sin Ai=ni± mi (243)
где mi– CKO каждой линии.
В этих уравнениях два неизвестных, но наличие ±mn приводит к тому, что прокладка (решение) двух или более таких полос положения дает не точку, а площадь положения, внутри которой с определенной вероятностью, находится место судна, сама же площадь оценивает точность этого места. Если линий три и более, то место судна отыскивается по методу наименьших квадратов (МНК). Для оценки точности места можно применить: эллипс ошибок, среднюю квадратическую ошибку М места, называемую также круговой или радиальной ошибкой (радиус круга ошибок), и, наконец, СКО обсервованных координат mφи mλ. Применение этих оценок рассмотрим ниже для двух, трех и более линий.
Вес точки пересечения высотных линий. Для удобства выбора места по МНК и сравнения нескольких мест вводится понятие веса, Вес точки пересечения двух ВЛП (i и j) определяется по формуле, известной из теории ошибок,
Pi,j=pipj sin2∆Ai,j |
(244) |
где pi и pj– веса линий i и j, определяемые по формулам (241).
Из формулы (244) видно, что чем точнее линия и ∆A ближе к 90°, тем точнее место и ему придается больший вес. По формуле (244) составлена таблица 11-а – для произведений весов (при m1=1 и равноточности линий) и табл. 11б6 для величин sin2∆A. Перемножая данные таблиц, получим веса точек
349

пересечения линий.
Из табл. 11-а,б видно, как сильно влияет средняя квадратическая ошибка линии на вес места, например при дневных наблюдениях Венеры и Солнца у хорошего наблюдателя mn=±0,4', что при угле 30° дает Р=18; это больше, чем для трех звезд при mn=±0,7' и ∆A=60° (Р– 9).
Таблица 11-а
mi |
±0,3' |
0,4' |
0,5' |
0,6' |
0,7' |
0,8' |
0,9' |
1,0' |
1,1' |
1,2' |
1,5' |
|
|
|
|
|
|
|
|
|
|
|
|
pi |
11 |
8,6 |
4 |
2,8 |
2,0 |
1,6 |
1,2 |
1,0 |
0,83 |
0,69 |
0,44 |
|
|
|
|
|
|
|
|
|
|
|
|
pi pi |
123 |
74 |
16 |
7,7 |
4,2 |
2,4 |
1,5 |
1,0 |
0,68 |
0,48 |
0,20 |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 11-б
∆Ai |
12° |
22° |
30° |
36° |
42° |
48° |
53° |
60° |
67° |
76° |
90° |
|
|
|
|
|
|
|
|
|
|
|
|
sin2∆Ai |
0,05 |
0,15 |
0,25 |
0,35 |
0,45 |
0,55 |
0,65 |
0,75 |
0,85 |
0,95 |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
Для выбора места в фигуре погрешностей удобнее оперировать с целыми числами, поэтому А.П.Ющенко предложил принять mi=mj=1 и умножить формулу (244) на 10; получим
|
|
|
|
|
|
|
|
|
|
|
|
Р=10 sin2 ∆А |
|
|
|
|
|
|
|
|
(245) |
|||||||||
По этой формуле составлена табл. 12, применяемая для выбора места по |
||||||||||||||||||||||||||||||
методу весов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆А |
0° |
12° |
22° |
30° |
36° |
42° |
48° |
53° |
60° |
67° |
76° |
90° |
104 |
113 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
° |
°... |
|
||
|
Р |
|
0 |
|
I |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
10 |
10 |
9 |
… |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для приближенных расчетов запомним, что с 30 до 67° вес меняется на 1 через 6°.
Пользуясь весами, можно рассчитать также и СКО (М) места по формуле
350

M = |
[ pi, j ,... ] |
(246) |
||
[P |
, j ,... |
] |
||
|
i |
|
|
|
где pi,j.– веса линий; рассчитываются по формуле (241) или табл. 11-а; Pi,j – веса точек пересечения линий (по табл. 11-а, б).
Понятие веса применяется также при осреднении нескольких обсерваций, каждой из которых придается вес р=1:M2, а средневзвешенное место определяется центрографическим приемом.
Две высотные линии. Оценка точности места. При двух линиях вероят-нейшее место принимается в точке их пересечения, а точность полученного места оценивается одним из трех приемов.
Оценка точности места эллипсом ошибок. Принимая, что линии равноточны и что полуось а направлена всегда по линии среднего азимута Aср (иногда она будет малой полуосью), получим следующие формулы для полуосей эллипса ошибок:
a = |
mn |
|
; |
b = |
mn |
|
(247) |
2 cos |
∆A |
2 sin |
∆A |
||||
|
|
2 |
|
|
|
2 |
|
Приемы построения эллипса ошибок рассматривались в общем курсе теории ошибок; здесь рассмотрим только приближенный прием построения эллипса для двух высотных линий. Между линиями строятся две биссектрисы углов их пересечения (рис. 127); одна из линий, например I—I, смещается параллельно на величину у=0,7mn, где mn получено для данных наблюдений [формула (239)], или принята априорно (см. §59). Линия I'—I' дает на биссектрисах точки А и В, определяющие концы осей а и b. Нанеся по ним точки А' и В', вписываем эллипс от руки.
Вероятность нахождения места в полученном среднем эллипсе около 39%. Такая вероятность недостаточна для обсервации, поэтому оси эллипса увеличивают. В табл. 13 показано, с какой вероятностью данный эллипс, построенный при М0, «накрывает» истинное место судна.
Иногда предельным называют эллипс с полуосями 2,5 а, b, Обычно при
351

построении эллипса достаточно удвоить его оси. Оценка точности места эллипсом ошибок для двух линий – наилучшая и достаточно простая.
Рис. 127
Оценка точности средними квадратическими ошибками координат. По формулам (224) для приращения координат ∆φ и ∆λ, получим ошибки mφ и mλ как ошибки линейных функций:
m2 |
= |
|
|
1 |
|
(m2 sin2 |
A |
|
+ m2 sin |
2 A ) |
|
||
|
|
|
|
|
|||||||||
ϕ |
|
|
sin2 |
∆A |
1 |
2 |
2 |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
(248) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
= |
|
|
1 |
|
(m2 cos A |
+ m2 cos2 |
A |
) |
|
|||
|
|
2 |
|
|
|||||||||
λ |
|
|
sin |
∆A |
2 |
1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где m1 и m2– СКО первой и второй линий.
Оценка точности места его средней квадратической (радиальной) ошибкой. Величина СКО места определяется по формулам теории ошибок:
М = a2 + b2 = m2 |
+ m2 |
= |
1 |
m2 |
+ m2 |
(249) |
ϕ |
W |
|
sin ∆A |
1 |
2 |
|
|
|
|
|
|
|
|
или при равноточных линиях, т.е. при m1=m2– mn, получим |
|
|||||
|
|
|
|
2mn |
|
|
|
|
|
M = sin ∆A |
(250) |
||
Вероятность нахождения места в круге радиуса М меняется с изменением ∆A; так, при ∆А=30° вероятность 60%, при ∆А=90°–63%. Вероятность может быть подсчитана по табл. 1-в МТ—75, как показано в инструкции к ним.
Выбор места и оценка его точности при трех и более ВЛП. Для выбора места в фигуре погрешностей, образовавшейся от случайных ошибок vi в линиях, применяется метод наименьших квадратов – в аналитической форме при решении на ЭВМ и в графической форме «приема весов» при графической
352
прокладке.
Аналитический вариант МНК. Метод наименьших квадратов рассматривался подробно в теоретических основах судовождения, поэтому покажем только его применение к высотным линиям. Если ∆ отсутствует, а число уравнений (242) больше числа неизвестных ∆ и ∆W, т.е. три и больше, то линии «уравниваются» и получаются более точные – вероятнейшие координаты. Обозначим в уравнении (242) cos A=а и sin A=b; получим систему
из N уравнений с двумя неизвестными и ошибками vi. |
|
|
|||||
|
a1∆ϕ + b1∆W − n1 = v1 |
|
|
|
|||
|
a2∆ϕ + b2∆W − n2 = v2 |
|
|
||||
|
|
(251) |
|||||
|
................................. |
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
aN ∆ϕ + bN ∆W − nN = vN |
|
|||||
|
|
|
|
|
|
|
Таблица 13 |
|
|
|
|
|
|
|
|
Название эллипса ошибок |
|
|
Величины полуосей |
|
Вероятность нахож- |
||
|
|
|
|
|
|
|
дения места внутри |
|
|
|
а |
|
b |
|
|
|
|
|
|
|
|
|
эллипса в % |
|
|
|
|
|
|
|
|
Средний квадратический |
|
|
1 |
|
1 |
|
39,3 |
(стандартный) |
|
|
|
|
|
|
|
— |
|
1,5 |
|
1,5 |
|
67,5 |
|
Удвоенный |
|
2 |
|
2 |
|
86,5 |
|
— |
|
2,5 |
|
2,5 |
|
95,6 |
|
Утроенный (предельный) |
|
3 |
|
3 |
|
98,9 |
|
Решая эту систему при условии
∑vi2 =[vv] = min или ∑pivi2 = min (252)
получим вероятнейшие значения ∆φ и ∆W. Для выполнения решения уравнения (251) возводятся в квадрат и складываются почленно. Для отыскания минимума [vv] полученное выражение поочередно дифференцируется по двум переменным и полученные уравнения приравниваются нулю. В результате преобразования получаются два уравнения с двумя неизвестными, называемые нормальными уравнениями:
∆ϕ[aa] + ∆W[ab] =[na]
(253)
∆ϕ[ab] + ∆W[bb] =[nb]
353

где квадратными скобками обозначены суммы произведений, например
[aa] = a2 |
+ a2 |
+...;[ab] = a b + a |
b |
+...;[na] = n a + n |
a |
2 |
+... |
|||||||||||||
1 |
2 |
1 |
1 |
|
|
2 |
|
2 |
|
|
|
|
|
1 |
1 |
2 |
|
|
||
Решая эти формулы обычным путем [см. формулы (224)], получим |
||||||||||||||||||||
вероятнейшие значения ∆φ и ∆W: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∆ϕ = [bb][na] −[ba][nb] |
|
|
|
|
|
|||||||||||||
|
|
|
|
[aa][bb] +[ba] |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(254) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆W = [aa][nb] −[ba][na] |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
[aa][bb] −[ba] |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
После чего |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ0 =ϕc + ∆ϕ |
|
|
|
|
|
(255) |
|||||||||||
|
|
|
λ |
0 |
= |
λ |
c |
+ ∆λ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где
∆λ = cos∆Wϕ
Если линии положения неравноточны, то для каждой из них вычисляется свой вес р и вводится в каждую сумму произведений.
Подобное аналитическое решение применялось в ряде алгоритмов для
ЭВМ.
Центрографический прием отыскания вероятнейшего места. В этом варианте МНК уравниваются не линии, а вершины фигуры ошибок или аналитически– координаты ∆φi,j и ∆Wi,j точек попарного пересечения линий. После прокладки N линий образуется Q точек их попарного пересечения:
= N(N −1)
Q (256) 2
Так, при четырех линиях точек пересечения шесть, при пяти – 10 и т.д. В центрографическом приеме каждой точке пересечения – вершине– приписывается вес Рi,j по формуле (244) и вершины уравниваются по методу наименьших квадратов. В результате получаются вероятнейшие ∆φ и ∆W:
354
|
∆ϕ = |
[Pij ∆ϕij ] |
|
|
|
||
|
|
|
|
|
|
|
|
|
[P |
] |
|
|
|||
|
|
|
ij |
|
|
|
(257) |
|
|
|
[P ∆W |
] |
|||
|
|
|
|
|
|||
|
∆W = |
ij |
ij |
|
|
||
|
|
|
|
|
|||
[P ] |
|
|
|||||
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 128 |
Рис.129 |
Затем по формулам (255) вычисляются вероятнейшие φ и λ. Этот аналитический прием переработан в простой графический прием весов, которым и будем пользоваться в дальнейшем.
Графический прием весов. Основой графического приема служит способ сложения весов вершин обратно пропорционально их весам; он одинаков с отысканием центра тяжести фигуры. Вероятнейшее место M1 отыскивается в следующем порядке.
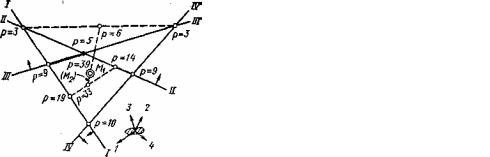
1.Произвести прокладку линий на карте или листе бумаги. Наметить точки пересечения линий попарно и получить ∆А вершин. Например, на рис. 128 проложены три линии положения, ошибки которых приняты одинаковыми (получен ∆ABC ошибок; ∆А сняты с прокладки).
2.По формуле (244) или табл. 11 получить веса вершин фигуры ошибок. Для равноточных линий веса зависят только от ∆А и по табл. 12 равны: Р3,2=8;
Р1,З=10; Р2,1=1.
3. На прямой, соединяющей вершины, например на стороне АС, найти точку R, отстоящую от вершин обратно пропорционально их весам. Вес ее
355

равен сумме весов вершин, т.е. PR=P1,2+Р2,3=9. На рис. 128 сторона АС делится на девять частей и точка R принимается в расстоянии одной части от A и восьми частей от С. Отстояние х точки R от одной из вершин можно определить в частях или в миллиметрах по формуле
x = P2,1 AC
P2,3 + P1,2
которую удобно решать по логарифмической линейке. В числителе выгоднее брать меньший вес, тогда х равно расстоянию от вершины с большим весом.
4. Полученную точку R соединить со следующей вершиной и аналогично предыдущему найти точку R1 (Р=19). Для трех линий эта точка и есть вероятнейшее место. Если вершин больше, то продолжаем далее, пока не будут учтены все вершины. Последняя точка RK и даст вероятнейшее место М1.
Максимальный вес точки М1 по табл. 12 при определении по трем линиям получается при ∆А=60° или ∆А=120° во всех линиях и равен Ркакс=22,5≈22, в то время как по двум линиям Рмакс=10.
При четырех линиях положения (рис. 129) прием весов применяется аналогично показанному для трех линий, но учитываются веса всех точек пересечения линий (от 4 до 6).
Например, на рис. 129 имеем шесть точек пересечения линий (вершин), веса которых выбраны из табл. 12. Сложив их по изложенному правилу, получаем вероятнейшее место в точке M1, слегка смещенной из середины четырехугольника1 (вес ее Р=39). Наибольший вес для определения по четырем линиям получается при ∆А=90° во всех линиях и равен 40, т.е. почти в два раза больше, чем по трем линиям.
1 Точка М2 получена по методу биссектрис
356

Описанный центрографический прием весов – простой и универсальный способ получения вероятнейшейточки при любом числе линий; применяется он и при объединении обсервованных мест.
Прием антимедиан при определении ее вероятнейшего места по трем высотным линиям. Этот прием является геометрическим следствием одного варианта МНК и применим при трех равновесных высотных линиях (т.е. если ошибки линий одинаковы). Выполнив прокладку трех линий и получив треугольник ошибок, вероятнейшее место получаем в точке пересечения двух антимедиан треугольника (рис. 130). Антимедианой называется зеркальное отражение медианы в биссектрисе. Она строится следующим образом. Проведем из вершины В медиану стороны АС и.отметим более острый <В', образованный ею со стороной ВС. Отложим <В' от другой стороны ВА этого угла треугольника и проведем прямую ВК'– это и будет антимедиана. Построив аналогично вторую антимедиану АК", в точке пересечения этих антимедиан получим вероятнейшее место M1. Сравнивая с решением этого примера методом весов, видим, что места M1 совпадают.
Оценка точности места при трех, четырех и более ВЛП. При
аналитическом определении вероятнейших координат по МНК можно получить также и элементы эллипса ошибок или радиальную ошибку места М (см. §92 и приложение 7). Однако при трех и более линиях вычислитель основное внимание обращает на надежность обсервации, т.е. на выявление промаха и исключение систематических ошибок (см. §75), оценку же точности места для практики достаточно производить круговой (радиальной) ошибкой М, тем более, что эллипс в этих случаях близок к кругу ошибок.
При графической прокладке более простым является расчет радиальной ошибки М по весам [формула (246)]:
M = |
[ pi] |
|
|
[P |
] |
|
i, j |
|
357 |
|
|
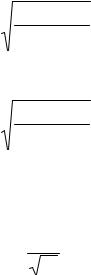
где веса pi линий и Pi,j точек пересечения линий определяются по табл. 11
или формуле (244). |
|
|
|
Для трех равноточных линий эта формула примет вид |
|
||
M = mn |
3 |
|
(258) |
∑sin2 |
∆A |
||
Для четырех равноточных линий получим |
|
||
M = mn |
4 |
|
(259) |
∑sin2 |
∆A |
||
При равномерном распределении светил по всему горизонту вместо этих формул получим удобную для запоминания приближенную формулу
M = |
2mn |
(260) |
|
N |
|
По этой формуле для трех линий имеем М=1,2 mn, для четырех М=mn. Этими радиусами строятся круги ошибок около выбранного
вероятнейшего места. Вероятность нахождения действительного места в заданном круге определяется по табл. 1-в МТ– 75, как показано в инструкции К-МТ.
§74. ОТЫСКАНИЕ МЕСТА ПРИ ПРЕДПОЛОЖЕНИИ
ОСУЩЕСТВОВАНИИ В ВЛП ПОВТОРЯЮЩЕЙСЯ ОШИБКИ ∆
В§72 мы установили, что большая повторяющаяся ошибка во всех линиях встречается редко (и всегда с обязательной случайной ошибкой v), но ее появление все же возможно. В этом случае для получения места уравнения ВЛП запишем в идеализированном виде, предположив, что v=0 и имеется только ∆:
∆φ cos Ai+∆W sin Ai =ni +∆ |
(261) |
Для определения неизвестных ∆φ, ∆W и ∆ теперь |
требуется три |
уравнения (261), которые и решаются алгебраическими приемами. Однако это
358

решение получено для нереального предположения u=0, поэтому представляет частный – теоретический случай решения в противоположность МНК. Полученное место М2 представляет также крайнее теоретически возможное место, а не действительное место судна, как иногда считают.
Решение уравнений (261) при наличии ∆ можно выполнить образованием их разностей, при этом исключается ∆. В графическом варианте этот прием приводит к применяемому на практике методу астрономических биссектрис.
Метод астрономических биссектрис. Если в линиях I–I и II–II (рис. 131)
имеются одинаковые величины (+∆), то смещенные линии I'–I' и II'–II' дадут в пересечении место М2. Вводя величины «–∆», получим М'2 и. т.д. Эти места лежат на прямой Б–Б', называемой астрономической биссектрисой, она делит угол между линиями в направлении среднего азимута (Aср на рис. 131). Првще всего ее построить, если при М0 провести стрелки I и 2 в направлении на светила (по их азимутам) и разделить указанный ими угол между ВЛП пополам.
Уравнение астрономической биссектрисы. Если записать два уравнения
(261) и из второго вычесть первое, то ∆ исключится и после преобразований получим
∆φ cos (Acp+90O)+∆W sin(Acp+90O)=l
где l = 12 (n2 − n1 )cosec∆A
Эта формула представляет уравнение разностной линии положения (см. табл. 8) или астрономической биссектрисы, которую можно построить по τ=Aср+90° и переносу l (см. рис. 131). Учитывая, что биссектрисы построены по линиям, содержащим случайные ошибки v, оцениваемые ±mn, получим, что ошибка mб астрономической биссектрисы выражается формулой
m |
б |
= mn |
cosec ∆A |
(262) |
|
2 |
2 |
|
|
|
|
|
Из формулы (262) видно, что ml изменяется от 0,7mn при ∆А=180° до ∞ при ∆А=0°, т.е. биссектрисы точны при угле между линиями в 180° (при
359
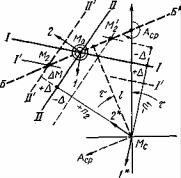
светилах в обратных азимутах) и менее точны при углах ∆А, меньших 90°; при ∆А≤45° ошибка превышает 2mn и биссектрисы неприменимы. Рассмотрим определение места этим методом.
Рис. 131
При определении места по двум ВЛП получается одна астрономическая биссектриса, она указывает направление Б–Б', в котором могут быть смещены места при наличии повторяющейся ошибки ∆ (см. рис. 131). Ошибка ∆M места определится по формуле (228). При ∆h1=∆h2=∆ получим
∆M = ∆sec |
∆A |
(263) |
|
2 |
|||
|
|
Из этой формулы видно, что ошибка ∆M меньше при ∆А<90°.
При определении по трем линиям (при наличии ∆) получается треугольник ошибок (рис. 132, а), решение которого методом астрономических биссектрис имеет два случая:
—светила наблюдались в разных частях горизонта (∆Акр>180°). Построив две астрономические биссектрисы (рис. 132,а), в точке их пересечения (внутри треугольника) получаем место M2, а величина ∆ равна радиусу вписанного круга, знак ∆ – по направлению смещения линий [на рис. 132, а (+∆)];
—светила наблюдались в одной части горизонта (∆Aкр<180°). Точка пересечения биссектрис оказывается вне треугольника (рис. 132, б). В ней и принимается место М2; ошибка ∆ равна радиусу касательной окружности, знак
360
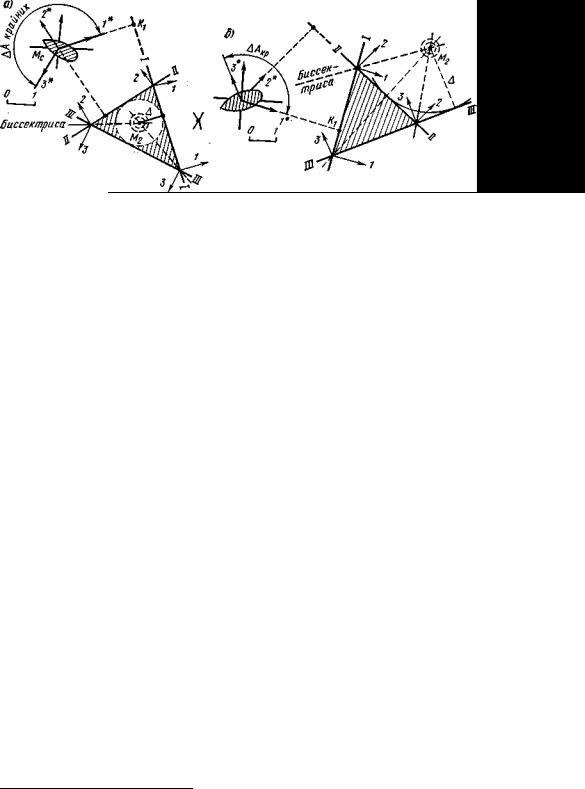
ее – по направлению смещения любой из линий. Из рис. 132 видно, что при трех линиях только одна биссектриса – независимая, две другие зависимы от уже примененных линий, что делает положение этих биссектрис не вполне надежным, особенно от промаха (см. рис. 134).
Рис. 132
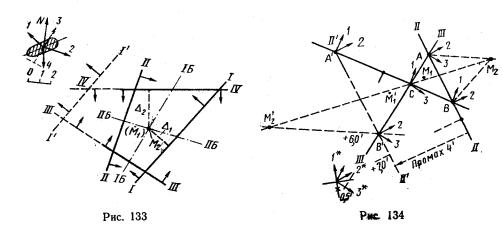
При определении по четырем ВЛП наличие ∆ приводит к образованию четырехугольника ошибок (рис. 133). Знак и величина ∆ могут быть обнаружены только, если светила наблюдались по всему горизонту и в обратных азимутах. В этом случае биссектрисы строятся между линиями, взятыми попарно – с ∆A ближе к 180°, т.е. для стрелок, расположенных «обе наружу», или «обе внутрь». Биссектрисы IБ и IIБ (см. рис. 133) можно проводить только, если все стрелки расположены одинаково – для пары I–II «обе внутрь» (наружу) и для пары III–IV– «обе внутрь» (наружу). Это означает, что если ошибка одинакового знака, ее можно принять за ∆. На рис.133 показана пара I'–II со стрелками «наружу» и пара III–IV со стрелками «внутрь», для них применять метод биссектрис нельзя, так как ошибка имеет разный знак1.
По биссектрисам IБ и IIБ получается место М2, а величина ошибки определяется по формуле
∆ = |
1 |
(∆1 + ∆2 ) |
(263') |
|
2 |
|
|
1 Это может служить признаком промаха, см. §75.
361
где ∆1 и ∆2– расстояния по линии I и IV, знаки их – по смещению линии. При аналитическом решении неизвестные ∆1 и ∆2 вводятся в пары линий (с ∆А≈180°); после вычислений сравниваются их знаки, и при одинаковых по
формуле (263') выводится ∆.
Если четыре светила наблюдались в одной части горизонта, то решить, есть ли ошибка одного знака или это действие случайных ошибок или промахов, нельзя, поэтому метод биссектрис применять в этом случае не следует.
Аналогично анализируется место, полученное по астрономическим биссектрисам при пяти и шести линиях.
Возможности применения метода биссектрис. В реальных условиях одинаковая ошибка ∆ во всех линиях встречается редко, однако уже одинаковый знак в ∆ дал бы возможность приближенно применять метод биссектрис. Поэтому прежде всего следует установить, есть ли ошибка одного знака, — по анализу направления стрелок, показанному выше в п. 3 для четырех линий, т.е. обе внутри или обе наружу. Но такой анализ возможен только для четырех и более линий. При трех линиях невозможно выявить не только одинаковую ∆, но даже ошибки одного знака. Более того, если в одной (тем более – в двух) из линий сделан мелкий промах (например, вместо ∆hφ=–2' приняли +2') или допущена ошибка при измерении высот вне вертикала, то метод биссектрис дает грубо неверное место– с увеличением промаха в несколько раз. На рис. 134 показано место М2, полученное по треугольнику ABC методом биссектрис и место М1 – по МНК. Если в линии II допущен указанный промах на 4', линия займет положение II', а треугольник перевернется (А'В'С') и метод биссектрис даст место M 2' , отстоящее от M2 на
12'; метод СНК дает M1' , отстоящее от М1 на 2,1'. Следовательно, при выборе места по методу биссектрис и промахе в линии промах в результате увеличивается, а по МНК – уменьшается.
Подобная же опасность возникает и без промаха – за счет случайных ошибок. При введении ∆ мы пренебрегли ими, а их неизбежное присутствие
362
может привести к картине, аналогичной промаху.
Выводы. 1. Метод астрономических биссектрис можно применять для получения φ0, λ0 и ∆ только при четырех (и более) линиях, наблюденных в разных частях горизонта после установления, что в линиях есть ошибка одного знака. Графический прием дает такую возможность еще до выбора места.
2. При трех ВЛП метод астрономических биссектрис следует рассматривать как теоретический прием получения крайнего решения – места М2, которое может понадобиться при выборе места с учетом всех факторов, например если это место ближе к опасности или для применения обобщенного МНК наряду с местом M1. Применять его при трех линиях как отдельный прием не следует.
При двух ВЛП метод биссектрис дает направление (Б—Б' на рис. 131) по которому возможны смещения мест при появлении общей повторяющей ся ошибки; это используется при планировании и анализе обсерваций.
Влияние постоянной ошибки во времени. Если во всех линиях есть одинаковая ошибка во времени, например от неправильной поправки хронометра (∆Tхр=∆u), то вычисляемые высоты и переносы n изменятся на разные величины: ∆hт=cosφ sin ∆ТХР' , но при прокладке или при решении уравнений (223), в которых вместо n подставлены ∆hт, по формулам (224) получим
∆φ=0; ∆λ= ∆ТХР' |
(264) |
т.е. вследствие общей ошибки во времени место сместится только по
363
долготе на величину ошибки ∆ТХР' при любом числе линий (к Оst при – ∆T и к
W при +∆T). Это обстоятельство следует учитывать при анализе обсервации.
75.ОТЫСКАНИЕ МЕСТА СУДНА И ОЦЕНКА ЕГО ТОЧНОСТИ ПРИ СОВМЕСТНОМ ДЕЙСТВИИ ОШИБОК В ВЛП
Вреальных условиях в высотных линиях всегда есть случайные ошибки u, возможны промахи [γ] и иногда могут быть заметные систематические ошибки ∆ (ошибки поправок в пределах точности их определения есть всегда), поэтому уравнение линии примет вид
∆φ cos А+∆Wsin А=n+v+∆+[γ] |
(265) |
Сумма ошибок входит в перенос в виде индивидуальной ошибки лийии; эти ошибки после прокладки нескольких линий приводят к появлению фигуры погрешностей (треугольника или системы точек попарного пересечения линий). Обычно решить заранее, от преобладания каких ошибок возникла фигура погрешностей, затруднительно. Это затрудняет и аналитическое решение, так как в уравнении (265) много неизвестных и, кроме того, неизвестно, надо ли вводить ∆ и исключен ли промах. Для выхода из этого затруднения следует прежде всего так спланировать наблюдения – расположение светил, методику выполнения и число линий, чтобы создать критерии выявления ошибок в процессе и после обработки, а также применить методы выбора места (уравнивания), учитывающие все ошибки.
Методы, обработки, т.е. отыскания места и оценки его точности, должны обеспечить выявление промаха, исключение ∆ и получение вероятнейшего места. В настоящее время применяется два приема: графический прием комбинирования МНК и метода биссектрис; аналитический метод – обобщенный метод наименьших квадратов или МНК с учетом ошибок общих (для всех линий) поправок.
Графический прием комбинирования МНК и метода биссектрис. В
364
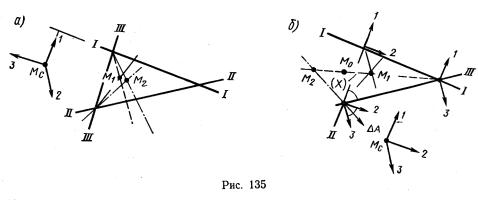
этом приеме после графической прокладки анализируются конкретные ошибки данного определения места, промахи выявляются сравнительным анализом величин переносов и фигуры погрешностей, получаются места М1 и М2 (рис.135) и обсервованное место выбирается исходя из обстановки: ближе к опасности или на основе статистических данных – посредине между М1 и M2. Оценка точности при двух линиях включает m∆ [формулы (266), (267)], особенность которой в том, что она действует всегда по линии среднего азимута. При симметричном расположении трех и более светил по всему горизонту m∆ в оценку точности не включается [см. формулу (260)].
Графический прием удобен при обычной ручной прокладке; его преимущество – анализ конкретных ошибок, недостаток – отсутствие общего аналитического решения, что нужно для ввода в программу ЭВМ. Рассмотрим применение этого приема к двум, трем, четырем и более линиям положения.
I. Определение по двум линиям положения. В этом случае данных мало и анализ ограничен. Место принимается в точке пересечения двух линий. Обнаруживаются только крупные промахи – по величине переноса [с помощью формул (238)], небольшие промахи – в 5–10' не обнаруживаются.
Данных для выявления систематических ошибок нет, можно указать только направление (Aср, см. рис.131), по которому они смещают место ( М2' и
М2'' ), это применяется при подборе условий наблюдений (см. §77).
Из сказанного вытекает, что место, полученное по двум линиям, не свободно от перечисленных ошибок и поэтому недостаточно надежно. Повысить его надежность можно только привлекая второго независимого наблюдателя, т.е. работающего с другим секстаном и хронометром, независимо от первого; он должен наблюдать светила в обратных азимутах (или те же светила, но через зенит).
Оценка точности полученного места. При оценке точности в этом случае надо учитывать СКО поправок (возможных повторяющихся ошибок) m∆. Для равноточных высотных линий имеем формулы:
365
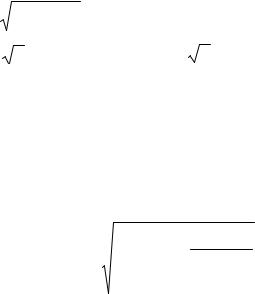
a = |
mn2 + m∆2 |
b = |
mn |
|
(266) |
||
|
|
; |
|
|
|||
2 cos |
∆A |
2 sin |
∆A |
||||
|
|
2 |
|
|
|
2 |
|
Полуось эллипса а направлена по линии среднего азимута; эллипс строится по полуосям.
Радиальная ошибка места может быть определена по формуле
Каврайского. |
|
|
|
|
|
|
|
M = |
2m2 |
+ |
m2 |
(267) |
|||
|
n |
|
∆ |
||||
sin2 |
∆A |
cos |
2 ∆A |
||||
|
|
|
|||||
|
|
|
|
2 |
|
||
|
|
|
|
|
|
||
Вероятность нахождения места в круге заданного радиуса определяется, как показано в §73.
II. Определение места по трем линиям положения. Прокладка трех высотных линий всегда дает треугольник ошибок (отсутствие его – частный случай комбинации ошибок). Треугольник является следствием совместного действия ошибок, поэтому его величина не указывает на преобладание тех или иных ошибок. Так, при разных систематических ошибках треугольник может быть малым, а при некоторых комбинациях случайных ошибок – большим. Исключение составляет случай, когда треугольник чрезмерно велик (стороны больше 15—20') – это указывает на промах в одной из линий, в какой именно, можно определить, пользуясь формулой (238). Мелкие промахи при трех линиях не выявляются и часто служат причиной «отскока» места.
Для отыскания места при наличии треугольника следует применить оба рассмотренных выше метода: МНК (M1) и астрономических биссектрис (M2). При расположении светил в разных частях горизонта (рис. 135, а) оба места оказываются рядом, поэтому принимается место М1, как более общий случай.
Самый спорный случай, вызвавший длительную полемику, получается при расположении светил в одной части горизонта (рис. 135, б). Место М1 определенное приемом весов, получается внутри треугольника, место M2– по методу биссектрис – вне треугольника. Решение о выборе места принимается
366
критерии:
—в соответствии с требованиями безопасности плавания принимается то место, которое ближе к опасности;
—когда требуется вероятнейшее место, надо учесть статистические данные экспериментов о величинах и действии ошибок, по которым при современном соотношении mn и m∆ получим: при двух острых углах треугольника (∆А меньше 45°) место принимается в М1 (по МНК); при больших ∆А место принимается между М1 и М2 (по современным официальным рекомендациям – посредине между ними в точке М0; см. рис. 135,б).
Оценка точности при определении по трем ВЛП. Если три светила расположены в разных частях горизонта, то для оценки точности применяются формулы (258) или (260). Если же светила наблюдались в одной части горизонта, то при выборе места вне треугольника следует учесть ошибки биссектрис, для чего с графика (см. рис. 138, Мбис) для данной ∆А снимается ордината и умножается на mn. Для ∆А=60° приближенно получаем М=2,2mn. Так как при трех линиях промахи и систематические ошибки не выявляются, для повышения надежности обсервации надо привлекать второго независимого наблюдателя, причем ему следует измерять высоты в обратных азимутах.
III. Определение места по четырем линиям положения. Наблюдать четыре светила следует обязательно попарно в обратных азимутах (см. §74).
367
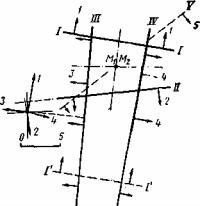
После прокладки четырех линий образуется фигура погрешностей с четырьмя, пятью или шестью точками попарного пересечения линий. Анализ расположения линий и размеров фигуры позволяет выявить промах и систематическую ошибку. При линиях положения расставляются стрелки в направлении азимутов светил (рис. 136). Если размеры сторон четырехугольника больше удвоенного критерия [формула (238')] (т.е. 3—7'), а все стрелки направлены одинаково внутрь или наружу от центра, то в линиях есть ошибка постоянного знака, а промахи, по-видимому, отсутствуют. При этом можно применить метод биссектрис и место М2 принять за М0 (оно близко к M1 но получается проще); систематическая ошибка определится по формуле
(263').
Рис. 136
Если же при таком же или еще большем четырехугольнике одна пара стрелок направлена внутрь, другая наружу (на рис. 136 II, I'), то возможен промах, но в какой линии, можно судить только по «отскоку» линии (так, на рис. 136 «подозрительной» является линия I'—I').Прэверка ее вычислений обычно выявляет просчет. Объективным критерием служит пятая линия (см.рис.136), наблюденная в промежуточном азимуте; ее можно до анализа не обрабатывать.
Если четырехугольник мал (менее 4mn), то при любом расположении стрелок промаха, очевидно, нет, преобладают случайные ошибки, поэтому
368
применяется МНК – по весам учитываются все шесть точек пересечения и место принимается в М1.
При наблюдении четырех ВЛП в одной части горизонта места М1 и М2 не совпадают и, так же, как и при трех линиях, место выбирается либо ближе к опасности, либо посредине между М1 и М2. В этом случае выявить ошибки одного знака и промахи также нельзя и обсервация не получается надежной. Вот почему надо наблюдать светила обязательно в обратных азимутах.
Оценка точности при определении по четырем линиям. Оценка точности производится радиальной ошибкой по формуле (260) или приближенно: М=mn. Место, определенное по четырем диниям, достаточно надежно, не у одиночного наблюдателя остается возможность ошибки во времени [см.формулы (264)], поэтому он должен после наблюдений вторично проверить время (например, остановить секундомер по другому хронометру или по сигналам времени, проверить uхр и часовые углы). Если привлекался второй наблюдатель, то среднее место отстоит от истинного обычно в пределах 0,5'.
При наблюдениях большего числа линий анализ производится аналогично, однако более пяти линий наблюдать нет смысла.
На основании проведенного анализа можно сделать следующее заключение.
1.Надежное место, т.е. обеспечивающее от промахов, систематических ошибок и имеющее достаточную точность, получается при четырех линиях, имеющих попарно обратные азимуты.
2.Определение по трем линиям дает возможность установить только грубые промахи, но не дает суждения о систематических ошибках. Для выбора места можно применить критерий близости к опасности или статистические данные. Поэтому обсервация по трем звездам не является вполне надежной.
3.Обсервация по двум ВЛП ненадежна и должна рассматриваться как ориентировочная.
4.К ответственным обсервациям следует привлекать двух независимых наблюдателей. Тогда можно ограничиться тремя ВЛП или двумя ВЛП у
369

каждого наблюдателя, которые следует наблюдать в обратных азимутах (например, через зенит).
Аналитический метод «обобщенный метод наименьших квадратов»
(понятие). Обобщенный метод наименьших квадратов представляет метод уравнивания зависимых наблюдений, т.е. уравнивания с учетом корреляции обсервованных высот, обусловленной ошибками общих поправок. В применении к задачам судовождения этот метод1 разрабатывали или исследовали В.В.Каврайский, В.Т.Кондрашихин, В.А.Коугия, М.И.Скворцов, Р.А.Скубко, А.Н.Раховецкий. В.В.Вейхман, Е.В.Якшевич, Б.И.Никифоров, Г.В.Макаров и др.
До уравнивания промахи в измерениях или поправках должны быть выявлены, например, пользуясь формулой (238).
В этом методе повторяющиеся ошибки поправок (см. §72) оцениваются их статистически полученными дисперсиями и величинами m∆ (в эту величину входят ошибки ∆d, ∆s, ∆i и личные ошибки наблюдателей). Так как в данной обсервации эти индивидуальные ошибки повторяются во всех линиях, то линии перестают быть независимыми. Однако связь между ними – вероятностная, так как применяются статистические оценки ошибок. При применении обычного МНК уравнения (251) включают только случайные ошибки v и принимаются независимыми; их обработка дает место M1 (см. §73). Если в уравнениях (261) присутствуют только повторяющиеся ошибки ∆, то получается место М2. В действительности уравнения линий включают и случайные и систематические ошибки (265) и в определенной степени зависимы. В общем виде зависимость линий определяется корреляционной матрицей, включающей mi. всех источников ошибок. В применении к линиям положения, по предложению В.Т.Кондратшихина, степень зависимости линий определяется отношением дисперсий случайных ошибок mn линий и ошибок m∆ поправок, т.е. величиной
λ |
mn2 |
, при этом матрица сведется к коэффициенту корреляции Кm, |
|
m∆2 |
|||
|
|
1 Теория этого метода разрабатывалась голландцем J. М. Tjenstra (1956 г.), Ю.А. Гордеевым (1960 г.) и др.
370
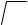
λ |
mn2 |
, при этом матрица сведется |
|
m∆2 |
|||
|
|
вычисляемому по формуле
Km =
к коэффициенту корреляции Кm,
1 |
(268) |
||
1 + |
mn2 |
||
|
|||
m∆2 |
|
||
|
|
||
Здесь величина mn может получаться из данных наблюдений или оцениваться априорно (см. §59); величина m∆ получается по средним статистическим данным (см. §72). По данным официальных руководств получаем km=0,3÷0,7: величина 0,3 принимается при работе с наклономером и новыми секстанами; 0,7– без наклономера и со старыми поправками s; практически линии принимаются равноточными. В обобщенном МНК уравнивание наблюдений, в данном случае высотных линий положения, производится также, основываясь на принципе наименьших квадратов (см. §73), но с учетом отношения ошибок mn2 ,m∆2 , т.е. коэффициента корреляции km,
по формуле
∑pivi2 + km[(N −1)∑pivi2 − (∑vi  pi )2 ] = min
pi )2 ] = min
Выполнив решение аналогично рассмотренному для МНК в §73 [см. формулы (253), (254)1, получим в общем виде:
∆ϕ = |
С1 E2 − E1С2 |
∆W = |
F1C2 − C1 E1 |
(269) |
|
N1 |
N1 |
||||
|
|
|
где N1=F1E1–E1; C1, E1, С2; E2; F1– коэффициенты нормальных уравнений, приведенные в приложении VII.
Далее по формулам (255) получаются вероятнейшие φ0 и λ0. Коэффициент корреляции km входит во второй член формул коэффициентов. При km=0 формулы (269) обращаются в (254), т.е. в обычный МНК, и получает место М1, при km=1 получается алгебраическое решение уравнений и место M2 по методу биссектрис, при этом можно вычислить и повторяющуюся ошибку. При промежуточных значениях km места располагаются на прямой М1М2 в зависимости от принятого km. Это обстоятельство позволило разработать
371
полученными графически, в расстоянии х=µМ1М2 от М1 (рис. 135, б), где µ определяется выражением
µ = |
|
|
|
1 |
|
mn |
2 |
∑sin2 ∆A |
|||
|
|
|
|
|
|
|
|
2 |
|||
1 + |
|
(∑sin ∆A) |
|||
|
m∆ |
|
|||
Различные авторы принимали разные данные о mn и m∆ при различных ∆A, отсюда в литературе появились рекомендации принимать х от 1/4 до 1/2 расстояния М1М2; по нашим данным не следует принимать х большим 1/3.
Формулы для оценки точности места, полученного по обобщенному МНК, также учитывают km, они приведены в приложении VII,4.
Алгоритм обобщенного МНК оказался удобным при решении задач определения места на ЭВМ. Он дает как общее– для средних условий– решение, так и крайние решения– места М1 и M2; это позволяет в условиях мостика выбрать место ближе к опасности, что при других, более жестких алгоритмах невозможно. Поэтому в современных навигационных ЭВМ применяется алгоритм обобщенного МНК (см. §92 и приложение VII). Можно предполагать, что в дальнейшем алгоритмы обобщенного МНК будут совершенствоваться в сторону учета не среднего km, а корреляционной матрицы, вывода ∆, а также выявления промахов.
При ручном решении задачи следует предпочесть рассмотренное выше графическое решение.
372
