
- •Введение
- •Глава 2. Параллактический треугольник светила и его решение
- •§4. Параллактический треугольник и его решение по основным формулам
- •§5. Вычисление высоты и азимута светила по системам формул
- •§7. Разложение высоты и азимута в ряд Тейлора. Теория таблиц численного типа
- •§1. Небесная сфера
- •§2. Системы сферических координат
- •§3. Графическое решение задач на небесной сфере
- •Глава 3. Видимое суточное движение светил. Изменение координат светил
- •§9. Характеристика суточного движения светил
- •§10. Явления, связанные с суточным движением светил
- •§11. Изменение координат светил вследствие видимого суточного движения
- •Глава 4. Обращение Земли вокруг Солнца. Видимое движение Солнца и изменение его координат
- •§13. Обращение Земли по орбите и видимое годовое движение Солнца
- •§14. Изменение экваториальных координат Солнца в течение года
- •Глава 5. Орбитальное и видимое движение планет, Луны и искусственных спутников
- •§18. Фазы и возраст Луны
- •§21. Орбитальное движение искусственных спутников
- •Глава 6. Измерение времени
- •§22. Основы измерения времени
- •§23. Звездные сутки. Звездное время. Основная формула времени
- •§26. Поясное, декретное, летнее, московское и стандартное времена, их связь с местной системой
- •§28. Понятие о точных шкалах времени
- •Глава 7. Вычисление видимых координат светил. МАЕ
- •§31. Понятие о вычислении видимых координат светил на ЭВМ
- •§32. Устройство таблиц МАЕ для расчета часовых углов и склонений светил
- •§33. Определение времени кульминации светил
- •§34. Обоснование расчета времени видимого восхода (захода) Солнца и Луны и времени сумерек
- •§35. Определение времени восхода и захода Солнца и Луны и времени сумерек по МАЕ
- •Глава 8. Измерители времени. Судовая служба времени
- •Глава 9. Звездное небо. Звездный глобус
- •§42. Устройство звездного глобуса, его установка. Понятие о других пособиях
- •§43. Решение задач с помощью звездного глобуса
- •Глава 10. Секстан
- •§44. Основы теории навигационного секстана
- •§45. Устройство навигационных секстанов
- •§46. Понятие об инструментальных ошибках секстана и их учете
- •§47. Понятие о секстанах с искусственным горизонтом
- •Глава 11. Наблюдения с навигационным секстаном
- •§48. Выверка навигационного секстана на судне
- •§50. Приемы измерения высот светил над видимым горизонтом
- •§53. Наклонение видимого горизонта. Наклонение зрительного луча
- •§55. Общий случай исправления высот светил, измеренных над видимым горизонтом
- •§56. Частные случаи исправления высот светил
- •§57. Приведение высот светил к одному зениту (месту) и одному моменту
- •§58. Определение средних квадратических ошибок поправок и измерения углов
- •§59. Определение средней квадратической ошибки измерения высот светил в море
- •Глава 13. Астрономическое определение поправки компаса
- •§60. Основы астрономического определения поправки компаса
- •§62. Пеленгование светил. Точность поправки компаса
- •§63. Определение поправки компаса. Общий случай
- •Глава 14. Теоретические основы определения места судна по светилам
- •§65. Общие принципы астрономического определения места
- •§67. Метод линий положения. Высотная линия положения
- •§72. Ошибки в высотной линии. Оценка ее точности и вес
- •Глава 16. Методы отыскания места судна и оценки его точности при наличии ошибок в высотных линиях
- •Глава 17. Определение места по одновременным наблюдениям светил. Общий случай
- •§76. Особенности определения места по одновременным наблюдениям светил
- •§77. Общий случай определения места по звездам
- •§78. Определение места днем по одновременным наблюдениям Луны и Солнца
- •§79. Определение места днем по одновременным наблюдениям Венеры и Солнца
- •§80. Определение места по одновременным наблюдениям Венеры, Луны и Солнца
- •Глава 18. Определение места судна по разновременным наблюдениям Солнца
- •§81. Особенности определения места по разновременным наблюдениям Солнца
- •§82. Влияние ошибок счисления и наивыгоднейшие условия для определения места по Солнцу
- •§83. Определение места по Солнцу в общем случае
- •§84. Определение места комбинированием навигационных и астрономических линий положения
- •Глава 19. Ускоренные способы обработки наблюдений
- •§86. Обзор приемов ускорения обработки наблюдений
- •§87. Прием перемещения счислимого места
- •§88. Определение места с предварительной обработкой (предвычислением) линий положения
- •§92. Решение астрономических задач на клавишных ЭВМ
- •Глава 20. Частные методы определения координат места судна
- •§93. Определение широты места по меридиональной и наибольшей высотам Солнца. Понятие о близмеридиональных высотах
- •§96. Определение координат места в малых широтах по соответствующим высотам Солнца
- •§97. Графический способ определения места при высотах Солнца, больших 88°
- •§98. Особенности определения места в высоких широтах
- •Глава 21. Перспективы развития методов астрономических определений в море. Краткий исторический очерк
- •§99. Понятие об астронавигационных системах и навигационных комплексах
- •§100. Краткий очерк истории мореходной астрономии
- •Список литературы

§59. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ КВАДРАТИЧЕСКОЙ ОШИБКИ ИЗМЕРЕНИЯ ВЫСОТ СВЕТИЛ В МОРЕ
Случайные ошибки при измерении высот зависят главным образом от видимости горизонта, определяемой его освещенностью и состоянием погоды, от качества секстана и от опытности и искусства наблюдателя. Точность измерения характеризуется СКО высоты mос или СКО среднего арифметического m0. Обычно вычисляется mоc по данной серии измерений, но при известных координатах места можно получить СКО исправленной высоты mh, а если учесть точность вычислений, то и СКО высотной линии mn. Эти величины в море могут быть определены следующими способами.
1.Когда истинное место судна неизвестно, то mос вычисляется по внутренней сходимости отсчетов секстана, двумя приемами:
— обработкой графическим приемом по формуле (187) и по «размаху»;
— вычислением по формуле (187) с приведением к моменту и зениту.
2.Когда истинное место судна известно, то ошибки определяются по отклонениям линий от «истинной». В этом случае выводится и систематическая ошибка ∆ и mh по следующим формулам:
σ |
i |
= h − h ; |
|
∆ = |
∑σi |
; v |
=σ |
–∆ |
|
|
|
||||||||
|
i |
ист |
|
|
N |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mh |
= |
∑vi2 |
|
|
|
(193) |
|
|
|
N − |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
||
где h — измеренная и исправленная высота; hист — высота, вычисленная для истинного места.
Величина mос (или mh) при различных условиях различна, поэтому ее следует определять при каждых наблюдениях и полученное значение вводить в
обработку и оценку точности места. Однако практически ее определяют время от времени при наличии возможностей и времени и полученные значения применяют в аналогичных условиях, т.е. фактически чаще применяется априорная оценка mh.
277
Априорная оценка mh по аналогии условий. При выполнении рядовой астрономической обсервации наблюдатель измеряет по три высоты светила или даже по одной, и вывести moc ему обычно не удается. В этих случаях можно рекомендовать приближенную оценку mос (mh) по аналогии условий наблюдений. Время от времени, в различных условиях, со своим секстаном, наблюдатель определяет mос и mh и с учетом данных других исследователей (см. табл. 10) и ошибок вычислений составляет личный набор оценок точности (mh), который и применяет в аналогичных условиях.
В тех случаях, когда представляется возможность вывести ошибку данного ряда одновременно с наблюдениями, рекомендуем применять графический прием «по размаху».
Определение mос по внутренней сходимости графическом приемом.
Для вывода ошибки mос измеряют серию из 9—11 высот и моментов с интервалом между измерениями не более 30—40c и получают φ, А, ПУ, V. Измеренные высоты возрастают или убывают вследствие суточного движения светил и движения судна; эти изменения высоты должны быть исключены, т. е- высоты приведены к одному моменту и зениту. Наиболее простой метод приведения высот к одному значению — это построение средней скорости изменения высоты в виде средней прямой между точками графика (рис. 98). График строят в крупном масштабе: в 1'—5 мм (или 1 см) и в 1с — 1 мм (на миллиметровой бумаге); по оси абсцисс откладывают ∆T секундомера (или хронометра) от начального; по оси ординат — отсчеты секстана также от начального. Между полученными точками на глаз с помощью прозрачной линейки проводят среднюю линию, наклон которой к оси абсцисс характеризует среднюю скорость изменения высоты от всех причин. Этот график можно использовать двумя приемами:
—измерить на чертеже все отклонения точек по ординатам от прямой в принять их за vi после чего по формуле (187) получить величину mос;
—более удобен метод размаха, для которого отыскивают наибольшее отклонение вверх (∆hмакс) и вниз (∆hмин), получают размах
278
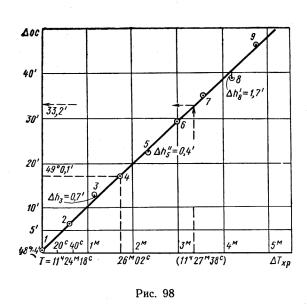
R=∆hмакс+ ∆hмин |
(194) |
после чего
mос=Rkp
где kp выбирают из табл. 7.
Критерий промаха. На графике отчетливо видны значительные отклонения некоторых точек от прямой. Прежде всего проверяют графические построения, и если они правильные, то отклонение ∆hмакс' проверяют на промах, как показано в §58. Образуется размах R1= ∆hмакс' +∆hмин и размах R2 со вторым отклонением ∆hмакс'' , разность их ∆R сравнивают с теоретическим ∆Rпред=R2 γN,
где γN выбрано из табл. 7. Если ∆R превысит теоретическое значение размаха,
то ∆hмакс' — промах, точка вычеркивается.
Построение графика и получение mос значительно ускоряется, если заготовить планшет со шкалами заранее.
Примечание. Если наблюдения производятся с помощником, то им одновременно наносятся точки на планшет и исключаются «отскочившие» наблюдения. В этом случае может помочь следующий прием предварительного построения прямой: перед самыми наблюдениями по МТ получают ∆hT и ∆hz и на графике строится теоретическая ∆h за 60c; от первого наблюдения можно провести прямую и контролировать отклонения от нее.
Пример 64. 4 мая 1977 г., следуя ПУ=277°, V=14 уз, около Тс=9ч30м (№=2W); φ=42°25' N; λ=30°50'W; ГКП=119° (—1°) измерили серию высот
279
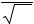
нижнего края Солнца ( ). Определить mос; m0 и проконтролировать на промахи.
Txp |
ос |
11ч 24м 18с |
48° 44,4' |
24 54 |
50,4 |
25 29 |
56,7 |
26 02 |
49 01,0 |
26 38 |
06,7 |
27 18 |
13,8 |
27 52 |
19,3 |
28 29 |
23,2 |
11Ч29М02С |
49° 30,7' |
Решение. 1. Строим график в масштабе: 1'=5 мм и 1c=1 мм (рис. 98). Начало отсчетов Т=11Ч24м18С и ос=48°44,0'.
2. Точка N=8 отскочила, но сравнительно немного. Проверяем на промах:
R1 = ∆h3 + ∆h8 = 2,4' R2=∆h3+∆h5=1,1' ∆R =1,3' ∆Rпред=R2γN=0,9'
Наблюдение 8 ошибочно, и его вычеркиваем. 3. moc=R2kp=(0,7 + 0,4)0,35=±0,4';
m0 = mNoc = ±0,15'
4. С графика (рис. 98) можно получить средний отсчет и момент или отсчет на нужный момент; например на 5-й момент ∆ос=23,0', т.е. ос=49°07,0'; Tхр=11ч26м38с; на 11ч27м38С ос=49°17,2' и т.п.
Определение mос по формуле (187) с приведением к одному моменту и зениту. Рассмотренный графический прием является все же приближенным. Более точный результат получается, если высоты аналитически привести к
одному моменту, вводя поправку hT=0,1 x K1∆Tc (см. §57), и к одному зениту,
вводя поправку hz=K2∆TМ. Отсчеты, исправленные этими поправками,
280
называют приведенными высотами hпp. Обычно высоты приводят к среднему моменту (Т5). Из приведенных высот вычисляют среднее арифметическое h0, затем ui=hпp—h0 и по формуле (187) получают mос.
Критерий промаха. Ошибочным следует считать то наблюдение, у которого отклонение u превышает 3m (причем m вычислена без подозреваемого наблюдения), т.е. u>3moc.
Пример 65. По данным примера 64 рассчитать mос и m0.
Решение. 1. Приведение к одному моменту. Из табл. 17 МТ—75 по
φ=42,4° N и А=62° SO выбираем: К1=1,63'/10с=; hT=0,163 Тс.
2. |
Приведение к одному зениту: |
|
|
|
|
|
|
|
||||
|
|
|
|
ИП |
|
118o из табл. 16 МТ-75 |
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
– |
|
277 ∆hV=–0,22’/1M |
|
|
||||
|
|
|
|
ПУ |
|
|
|
|||||
|
|
|
|
q |
|
201o ∆hz=–0,22∆TM |
|
|
|
|||
3. Вычисление производим по показанной ниже схеме; приведение |
||||||||||||
осуществляем к Т5 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Tхр |
|
∆TС |
∆hT |
∆hz |
|
|
ос |
hпр |
u |
u2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
11ч24м18с |
|
140е |
+ 22,8' |
-0,5' |
|
48° 44,4' |
49° 06,7' |
-0,5' |
|
0,25 |
|
|
24 54 |
|
104 |
+ 17.0 |
-0,4 |
|
50,4 |
7,0 |
-0,2 |
|
4 |
|
|
25 29 |
|
69 |
+ 11,2 |
—0,3 |
|
56,7 |
7,6 |
+0,4 |
|
16 |
|
|
26 02 |
|
36 |
+ 5,9 |
—0,1 |
|
49 01,0 |
6,8 |
—0,4 |
16 |
|
||
|
|
|
|
|
|
|
|
—0,5 |
25 |
|
||
26 38 |
|
00 |
0 |
0 |
|
49o06,7' |
6,7 |
|
||||
|
|
|
|
|
|
|
|
+0,2 |
|
4 |
|
|
27 18 |
|
40 |
- 6,5 |
+0,1 |
|
13,8 |
7,4 |
|
|
|||
27 52 |
|
74 |
-12,1 |
+0,3 |
|
19,3 |
7,5 |
+0,3 |
|
9 |
|
|
28 29 |
|
111 |
-18,1 |
+0,4 |
|
23,2 |
5,5 |
? |
|
— |
||
11ч29м02с |
|
144 |
—23,5 |
+ 0,5 |
|
49 30,7 |
|
+ 0,5 |
|
0,25 |
|
|
49 07,7 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h0 |
49o07,2’ |
∑u2=1,24 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
281
Примечание. Наблюдение 8 берем под подозрение и вычисления производим без него.
4. moc= |
1,24 |
= 0,177 = ±0,42' или moc=±0,4'; m0=±0,15'; |
|
7 |
|
Проверяем восьмое наблюдение: u8=1,7'>3moc=1,2'; следовательно, восьмое наблюдение действительно ошибочно.
Определение ошибок по отклонению линий положения от
«истинной». Способ дает самые достоверные результаты для mп и позволяет выявить систематические ошибки ∆. Его можно применять, когда место судна известно-с точностью выше 0,1', например по РЛС и точечным ориентирам, по спутникам, на рейдах или у причала, когда виден горизонт Измеряют 9—11 высот (допустимо 7), замечают моменты Tгр и снимают истинные координаты φ, λ. По полученным φ, δ, tм для каждого наблюдения вычисляют hист и вычитают ее из измеренной и исправленной высоты h; вычисления производят по формулам (193). Можно вычислять hист только для среднего момента, а все измеренные высоты приводить к этому моменту и зениту, как в примере 65, и далее по формулам (193) определять ∆ и mп.
Полученная представляет сумму ошибок от наклона секстана, в s, d и личную ошибку наблюдателя (см. табл. 10). Что касается величины т, то если расчет истинной высоты выполнять по таблицам ВАС или ТВА, в нее войдут ошибки вычислений и в результате получим mп. Если вычисления произведены точнее 0,05', например по ЭВМ, то получаем mh без ошибок вычислений. Рассмотренный прием дает штурману возможность проверить себя, инструменты и вычисления и получить уверенность в дальнейшей. работе.
Пример 66. 26/П 1975 г. на рейде Александрии автором измерены 7 высот Капеллы (h около 73°) секстаном СНО-Т № 44 35. Обработка велась по ВАС—58. Наклонение выбиралось из таблиц.
282
Решение.
h-hист |
u |
u2 |
|
+0,5' |
+0,4' |
+0,16' |
|
+0.2 |
+0,1 |
1 |
mn=±0,5’ |
-0,6 |
-0,7 |
49 |
M0=±0,2’ |
+0,7 |
+0,6 |
36 |
|
-0,2 |
—0,3 |
9 |
|
-0,3 |
—0,4 |
16 |
|
+0,4 |
+0,3 |
0,09 |
|
|
|
|
|
∆= +0,1' |
∑u2 |
1,36 |
|
|
|
|
|
283
