наблюдений, после исправления за счет ошибок инструмента и рефракцию называют видимыми местами (координатами) звезд.

Если координаты звезды α0, δ0 из каталога (они называются средними) известны на некоторый начальный момент (эпоху), то на любой другой момент ее видимые координаты α*, δ* могут быть рассчитаны по формулам:

где t — число лет от начальной эпохи;

∆α и ∆δ — приращения координат, рассчитываемые, как показано выше (формулы даны в прилож. II).

Если в формулах (65) учесть только действие прецессии и собственного движения, то получим средние координаты или средние места звезд, которые и даны в звездных каталогах на определенную эпоху. Если учесть действие нутации, то получим истинные места звезд, а если учесть еще и поправки за аберрацию, то получим их видимые места, которые приводятся в МАЕ, предвычисленные на несколько лет вперед.

§21. ОРБИТАЛЬНОЕ ДВИЖЕНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ

Классификация орбит искусственных спутников Земли (ИСЗ).

Орбиты ИСЗ могут быть круговыми, эллиптическими, параболическими или гиперболическими (рис. 40) в зависимости от скорости v, сообщаемой аппарату при запуске. Большинство спутников движутся по эллиптическим, близким и круговым, орбитам, плоскости которых проходят через центр Земли. Вид кеплеровой орбиты ИСЗ определяется шестью ее элементами: i, Ω, ω, е, р t0 (см.§12 и рис.41). Первые пять элементов определяют положение орбиты пространстве, последний — положение ИСЗ на орбите. Ближайшая к Земле точка П орбиты, где скорость спутника наибольшая, называется перигеем, а ее проекция на Землю — перицентром; наиболее удаленная точка орбиты — апогеем (линия АП называется линией апсид). Проекция спутника да

97

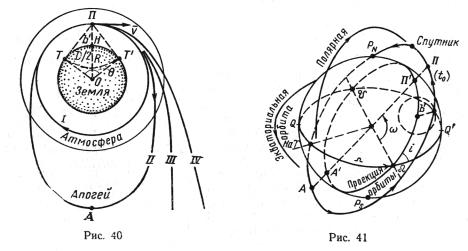
поверхность Земли (b') называется подспутниковой точкой или геозенитом (проекция светила на поверхность Земли называется полюсом освещения).

Орбиты ИСЗ классифицируются по углу наклона i, полуоси а, т.е. по высоте H над поверхностью Земли, и по эксцентриситету е. При i=0° орбита называется экваториальной (см. рис.41), при i=90° — полярной, при промежуточном угле i— наклонной. Угол наклона орбиты определяет районы движения спутника: при полярной орбите спутник может наблюдаться по всей Земле; при экваториальной — в районе экватора (в зависимости от H); при i<90° подспутниковая точка доходит до ω=i.

По высоте H над поверхностью Земли ИСЗ подразделяются на низкие — с высотой до 5 тыс. км (эти спутники быстроперемещающиеся) и высокие — более 5 тыс. км. Среди высоких выделяются стационарные спутники, запущенные в направлении с W-a на Оst на экваториальную орбиту с высотой H=35870 км (они «висят» неподвижно над одной точкой Земли). Высота H спутника определяет дальность его видимости и частоту прохождения в данном месте.

Скорости спутников и периоды их обращения. При выведении спутника на орбиту основными параметрами являются: высота точки выведения, скорость разгона и направление вектора скорости. Связь круговой скорости v1 с высотой можно получить из уравнения (54) или упрощенно, приравнивая силу тяготения центробежной силе:

98

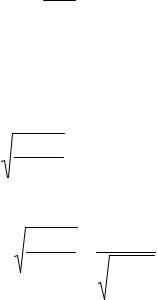
f Mmr2 = mvr 12

где r=R+H — расстояние до центра Земли; H — высота спутника.

Отсюда

или для Земли, подставляя R=6371 км, g0=9,81 м/с2, получим 7,91, км/с.

Первой космической скоростью v2 называется скорость тела, при которой но не упадет на Землю, а начнет вращаться около нее по круговой орбите, та скорость зависит от высоты спутника и поля тяготения, поэтому для разных планет она различна.

По известной скорости v1 можно определить период Т кругового

Из табл. 5 видно, что круговая скорость убывает с высотой спутника, На высоте 35870 км спутник движется с угловой скоростью Земли, и если его запустить с запада на восток, то получим стационарный спутник. Таков, например, советский спутник, запущенный 26/111 1974 г. (у него Т=23Ч46М).

Если скорость спутника при запуске больше круговой, но меньше

99

параболической, равной u2 2 , то орбита спутника будет эллиптической (см.

рис. 40, II). Большая полуось такой орбиты определяется соотношением высоты запуска и скоростью, сообщенной спутнику относительно круговой, т.е.

Период обращения ИСЗ по эллиптической орбите определяется из третьего закона Кеплера:

или

Т=1,66·10-4 а3/2

Например, спутники американской системы NNSS «Транзит» имеют v=7,25 км/с; а — около 7460 км (Н=1090 км) и Т=108м.

Для навигационных целей наиболее пригодными оказались быстроперемещающиеся ИСЗ, запущенные на почти круговые полярные орбиты (высота около 1000 км).

Если скорость аппарата при выводе на орбиту равна параболической, т.е.

v2=v1 2 , то его движение происходит по разомкнутой кривой — параболе (см рис. 40, III).

Второй космической скоростью v2 называется скорость, при которой тело начнет двигаться по параболе и обратно на Землю не возвратится. На уровне Земли v2=11,19 км/с, а на высоте 300 км — 10,93 км/с. Около других космических тел эта скорость иная, например около Луны v2=2,37 км/с, около Юпитера 60,19 км/с и т. п. Если скорость аппарата больше параболической, т.е. v>v1 2 , то его орбита — гипербола (см. рис.41, IV) и он еще скорее отойдет от Земли. Такие скорости придаются аппаратам, выводимым в солнечную систему при полетах на другие планеты. Показанные скорости справедливы только в сфере преобладающего притяжения Земли (радиус около 924 тыс. км). При

100

выходе аппарата из этой сферы он начнет двигаться под действием поля тяготения Солнца по эллиптической орбите, так как для Солнца эти скорости меньше параболической.

Скорость v3 тела, при которой оно двигается по параболе относительно Солнца и может уйти из солнечной системы, называется третьей космической скоростью. На уровне орбиты Земли v3=42,1 км/с, и, если скорость ракеты превысит эту величину, то она уйдет из Солнечной системы.

Зона видимости ИСЗ. Зоной видимости ИСЗ на земной поверхности называется малый круг ТТ' сферического радиуса D/2, описанный из подспутниковой точки b' (см. рис. 40 и 41). Зона видимости зависит от высоты спутника Н и рефракции радиоволн, излучаемых ИСЗ. Геометрическая зона видимости определится из треугольника ТОП, в котором

cos Θ2 = R +R H

Но угол θ= DR , поэтому

или

D=120arcsec 1 + H

R

Например, для ИСЗ с Н=1000 км D=3630 милям. Плоскость орбиты спутника сохраняет свое положение в пространстве (без учета возмущений), а Земля вращается, поэтому подспутниковая точка b' и зона видимости смещаются к западу с каждым витком спутника на

l=27, 8 sin i cosφT

Так, полярный спутник с высотой Н=1000 км в широте φ=0° смелется каждый виток на l=1580 миль, а в широте φ=60° — на 790 миль; через 13—14 оборотов этот спутник снова пройдет над данным районом. Сравнивая D с l, видим, что зона видимости больше смещения спутника, поэтому он может наблюдаться на экваторе два оборота, а в широте 60° — четыре оборота, т.е.

101

чем больше широта, тем чаще можно наблюдать спутник.

Продолжительность наблюдения спутника определяется временем прохождения зоны видимости через место наблюдателя. При центральном

прохождении ∆Т = 360ΘТо . К краям зоны это время уменьшается. Для

рассмотренного выше ИСЗ наибольшее время прохождения около 18м. Следовательно, для обеспечения достаточно частого определения места

по спутникам нужно запустить несколько спутников, синхронно движущихся, для непрерывного определения — 24.

Понятие о вычислении орбит и эфемерид спутников. Эллиптическая кеплерова орбита спутника определяется, как отмечалось, шестью элементами:

р; е; Ω; ; i; t0 (см. рис. 41). Эти элементы задаются при запуске спутника, а в процессе полета определяются по результатам наблюдений наземных станций слежения.

Расчет положения спутника, движущегося по кеплеровой орбите, ведется, как показано в §12, для планет. Однако в реальных условиях на спутник действуют различные возмущающие силы и его движение сильно отклоняется от простой эллиптической орбиты. Возмущения движения спутника подразделяются на возмущения, происходящие от гравитационных сил и от сил негравитационных. Наибольшие гравитационные возмущения происходят от несферичности поля тяготения Земли (эллипсоидальная форма и неравномерность распределения масс внутри Земли), меньшие — от влияния Луны и Солнца. Среди негравитационных сил наибольшая — это тормозящее действие атмосферы, меньшие — от электромагнитных явлений и от светового давления. Учет возмущений производится различными приемами, сейчас принят метод оскулирующих орбит в сочетании с поправками методом рядов.

Понятие об оскулирующих орбитах. Принцип оскулирующего движения заключается в приближенной замене малой дуги действительного движения соприкасающейся (оскулирующей) дугой кеплеровой орбиты. Следовательно, оскулирующая орбита представляет кеплерову орбиту, малая дуга которой

102

совпадает с малой дугой действительной орбиты. Если на ИСЗ подействовала малая возмущающая сила ∆t за короткое время ∆t, то вместо элементов орбиты р; е; Ω; ω... получим новые элементы р+ ∆р; е+ ∆е; Ω+ Ω∆ и т.д. Орбита представляет также кеплеров эллипс, но уже другой. Построив такие эллипсы для t+ ∆t; t+2 ∆t и т.д., получим непрерывное изменение эллипса под действием возмущающей силы; этот эллипс называется оскулирующим. Орбита теперь представляет систему точек, лежащих на различных оскулирующих эллипсах.

Изменение этих эллипсов представляется функциями р(t); е(t); Ω(t); ω(t) и т.д. Задавая потенциал возмущения, составляем дифференциальные уравнения —

ddtΩ; ddtω и т.п., решая которые, получаем в первом приближении скорости

изменения элементов орбиты ИСЗ. Так получается, например, главная часть изменения элементов Ω и ω эллипса оскулирующей орбиты. Получив —

ddtΩ; ddtω за один оборот спутника, вычисляют секундные и суточные их

изменения. Аналогично получаются изменения других элементов. Значения элементов на начало n-го оборота, средние скорости изменения элементов и точное время вводятся в запоминающее устройство ИСЗ, а оттуда транслируются в ЭВМ судна. По этим данным судовая ЭВМ вычисляет средние координаты спутника на данный момент.

Анализ изменения элементов показывает, что сжатие Земли влияет на положение орбиты в пространстве, а на форму и размеры орбиты практически не влияет. Так, оно вызывает движение восходящего узла в направлении навстречу движению спутника.

Для полярных орбит спутников движения узла не происходит, для экваториальных — движение наибольшее, около 9°/сут. Перицентр спутника также вращается в плоскости орбиты (почти равномерно) в направлении его движения, если i меньше 63°, и в обратном, если i больше 63°. При i=65° перицентр перемещается на 0,4°/сут. Вращение орбиты зависит от полуоси а; чем она больше, тем вращение медленнее.

103

Влияние негравитационных сил. Вследствие сопротивления атмосферы уменьшается скорость ИСЗ, положение же его орбиты не меняется. Постепенно уменьшаются эксцентриситет и полуось орбиты, спутник снижается, а орбита приближается к круговой. Наконец, в плотных слоях атмосферы спутник сгорает. Время его существования зависит от высоты орбиты, размеров и массы ИСЗ и колеблется от нескольких лет до сотен. Так, спутники системы «Транзит» должны существовать несколько десятков лет.

Учет влияния атмосферы совместно с другими мелкими причинами производится в общей теории возмущений. В основе ее лежит следующий метод: устанавливаются суммарные возмущающие функции; изменения координат разлагаются в ряды по степеням малого параметра, выявляют непериодические (вековые), периодические и смешанные члены и получают данные для предвычисления поправок координат. Полученные в наземном комплексе данные передаются в запоминающее устройство спутника и оттуда в ЭВМ судна. По этим данным вычисляют поправки к координатам, полученным по оскулирующим орбитам.

В американской системе NNSS эти данные передаются на спутник дважды в сутки. При прохождении спутника в районе судна последние данные об орбите и точное время принимаются судовым приемоиндикатором, вводятся в ЭВМ, где и вычисляются координаты спутника и результаты обсервации. В системе NNSS запущено шесть спутников; они имеют полярные орбиты, высоты над Землей 600 миль, периоды обращения 107—110м. Время между двумя прохождениями спутника в φ=0° равно 2Ч, в φ=45°—50м. Проход спутника длится 10—18м; за это время получают 5—7 серий определения места,

104