Готовимся к экзамену по математике_Крамор В.С_2008 -544с

К упражнению 1

1.Предел знаменателя дроби при x º 0 равен нулю. Поэтому непосредственно использовать теорему о пределе частно:о здесь нельзя.

2.Кроме то:о, данную дробь нельзя со ратить, а мы сделали это в предыдущем примере.

3.В данном случае числитель и знаменатель дроби следует умно-

жить на выражение 1 + x + 1, сопряженное знаменателю дроби. 4. В результате получим

З а м е ч а н и е. Считая, что lim 1 + x = 1, мы тем самым ис-

x º 0

пользуем свойство непрерывности фун ции y = 1 + x :

lim 1 + x = 1 + 0 = 1.

x º 0

К упражнению 1е

1. Пос оль у с символом × нельзя обращаться а с числом, нужно преобразовать данную дробь, например та :

Мы разделили почленно и числитель, и знаменатель заданной дроби на x2.

2. Теперь применим известные теоремы и найдем ис омый предел:

401

З а м е ч а н и е. Мы воспользовались тем, что:

К упражнению 1ж

1. Этот предел ле: о найти, если данную дробь предварительно соратить на x ;

2. В данном случае нужно обратить внимание на следующую важную особенность. Ко:да мы рассматриваем предел lim f(x), то обычно

x º a

предпола:аем, что фун ция f(x) определена во всех точ ах, достаточно близ их точ е x = a.

положительных значений x.

4.Поэтому при нахождении предела этой фун ции мы фа тиче-

си предпола:аем, что x º 0, оставаясь все время положительным.

З а м е ч а н и е. В подобных случаях :оворят не просто о пределе, а об одностороннем пределе.

К упражнению 2а

1. Здесь мы должны использовать определения степеней с дробным и отрицательным по азателями, а та же формулы дифференцирования суммы и степени. Напомним, что:

402

К упражнению 2в

1. Используя формулу для производной произведения двух фун - ций, получим

f′(x) = (x2(5x – 4))′ = (x2)′(5x – 4) + x2(5x – 4)′ =

=2x(5x – 4) + x2 · 5 = 15x2 – 8x.

2.Тот же результат получится, если сначала рас рыть с об и,

азатем выполнить дифференцирование.

В самом деле, имеем f(x) = 5x3 – 4x2 и, следовательно,

f′(x) = (5x3 – 4x2)′ = (5x3)′ – (4x2)′ = 15x2 – 8x.

К упражнению 2д

1. Здесь нужно использовать следующие формулы: а) производ-

4. На онец, подставив значение x0 = 2,5 в выражение (3), получим

y = 4 · 2,52 + 8 · 2,5 = 45.

403

К упражнению 4б

1. Найдем производную данной фун ции: f′(x) = –x4 + 10x2 – 9.

2. Приравняв производную нулю, получим уравнение

–x4 + 10x2 – 9 = 0, или x4 – 10x2 + 9 = 0. (1) 3. Положим x2 = y; то:да уравнение (1) примет вид

y2 – 10y + 9 = 0,

3.С дру:ой стороны, в результате двух повышений зарплата составила 1,32x.

4.Та им образом, получаем уравнение

x 1 + k 1 + k = 1,32x.

--------- ------

100 50

5. Корнями это:о уравнения являются числа k = –160 и k = 10. Со- :ласно условию, подходит толь о k = 10.

6. Ита , 2k = 20%.

К упражнению 8а

1. Запишем равенство ab = 81 в виде

2. Та а 3 = ac, то равенство (1) примет вид

ab = 34 = (ac)4 = a4c,

от уда

404

3. Нам нужно найти степень bb, или с учетом равенства (2), степень

4. Но 2 = bc, поэтому равенство (3) запишется та :

bb = (bc)4 = 24 = 16.

К упражнению 9б

1.Найдем ОДЗ неравенства: x l –7.

2.В зависимости от зна а правой части данно:о неравенства нужно рассмотреть два случая: x Ý [–7; –3) и [–3; +×).

3.Если x Ý [–7; –3), то правая часть неравенства отрицательна и,

405

неравенство (3) о:раничивает эти множества. Воспользуемся этим при

406

Т е м а 19

À

Касательная к графику функции. Скорость и ускорение в данный момент времени.

Применение производной к нахождению промежутков монотонности функции.

Критические точки функции, ее максимумы и минимумы. Общая схема исследования функции.

Задачи на отыскание наименьшего и наибольшего значений функции

Теоретичес ие сведения

1. Касательная к графику функции

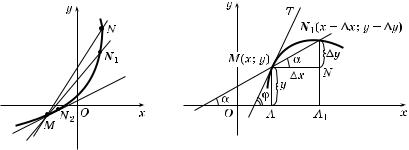
1°. Касательной ривой в данной точ е M называют предельное положение се ущей NM, о да точ а N стремится вдоль ривой точ е M (рис. 178).

2°. Используя это определение, найдем у ловой оэффициент асательной ривой в данной точ е. Пусть через точ у M(x; y) ривой, представляющей собой рафи фун ции y = = f(x), непрерывной в не оторой о рестности этой точ и (в лючающей точ у M), проведена се ущая MN1, образующая с по-

ложительным направлением оси Ox у ол α (рис. 179). То да из

407

треу ольни а MNN1 можно найти у ловой оэффициент этой

е M се ущая MN1 поворачивается во ру точ и M, причем

у ол α стремится у лу ϕ между асательной MT и положительным направлением оси Ox. В соответствии с определениемасательной получаем

Та им образом, у ловой оэффициент асательной рафи у фун ции равен значению производной этой фун ции в точ е а- сания. В этом за лючается еометричес ий смысл производной.

3°. Уравнение асательной ривой y = f(x) в заданной точ-е имеет вид

де (x0; y0) — оординаты точ и асания, (x; y) — те ущие

оординаты, т. е. оординаты любой точ и, принадлежащейасательной, а f′(x0) = k = tg α — у ловой оэффициент а-

сательной.

Примеры. 1. Составить уравнение асательной рафи у фун ции y = x2 – 2x в точ е с абсциссой x0 = 3.

Р е ш е н и е. Из уравнения ривой найдем ординату точ иасания: y0 = 32 – 2 · 3 = 3. Затем найдем производную и вычислим ее значение в точ е x0 = 3; имеем y′ = 2x – 2; f′(3) =

= 2 · 3 – 2 = 4. Теперь, зная точ у (3; 3) на ривой и у ловой о- эффициент f′(3) = 4 асательной в этой точ е, получаем ис о- мое уравнение:

y – 3 = 4(x – 3), или 4x – y – 9 = 0.

2. Дана ривая y = –x2 + 1. Найти точ у ее рафи а, в оторой асательная параллельна прямой y = 2x + 3.

Ре ш е н и е. Та а асательная параллельна прямой y =

=2x + 3, то их у ловые оэффициенты равны, т. е. k = y′(x) = 2.

Следовательно, –2x = 2, т. е. x0 = –1, а y0 = f(–1) = –(–1)2 + 1 = 0. Ита , (–1; 0) — ис омая точ а.

408

3. В а ой точ е ривой y = 3x асательная на лонена оси абсцисс под у лом 60°?

Р е ш е н и е. Находим y′(x) = (3 x )′ = (x1/3)′ = 1 x–2/3. Та

--

3

а по условию y′(x) = k = tg 60°, то

т. е.

x = (33/2)–3/2 = 3–9/4.

Остается найти ординату точ и асания: y = (3–9/4)1/3 = 3–3/4. Ита , (3–9/4; 3–3/4) — ис омая точ а.

2. Скорость и ускорение в данный момент времени

1°. Пусть точ а движется прямолинейно по за ону s = s(t),де s — перемещение точ и за время t, отсчитываемое от начально о момента времени. Этот за он называют за оном движения. Выберем а ой-либо момент времени t0 и рассмотрим

промежуто времени ∆t от момента t0 до момента t = t0 + ∆t. За

этот промежуто времени точ а переместится на величину ∆s = = s(t0 + ∆t) – s(t0). Средняя с орость точ и за промежуто вре-

мени [t0; t0 + ∆t] составляет

С уменьшением ∆t средняя с орость все точнее хара теризует с орость точ и в данный момент времени t0. Поэтому целесо-

образно определить м новенн ю с орость v(t0) в момент времени t0 а предел средней с орости vср при условии, что ∆t стремится нулю, т. е.

Ита , м новенная с орость точ и в данный момент времени равна значению производной от за она движения. В этом состоит физичес ий смысл производной.

409

2°. Очевидно, что м новенная с орость v(t) та же является фун цией времени. Поэтому можно рассмотреть с орость изменения с орости движения, т. е. ус орение прямолинейно о движения точ и:

a(t) = v′(t) = (s′(t))′ = s′′(t).

Ита , ус орение точ и в данный момент времени равно значению второй производной от за она движения. В этом состоит физичес ий смысл второй производной.

Примеры. 1. Найти с орость и ус орение точ и, движениеоторой происходит по за ону x(t) = kx + b.

Р е ш е н и е. Находим v(t) = x′(t) = k, a(t) = v′(t) = 0, т. е. с орость движения постоянна, а е о ус орение равно нулю. Та-ое движение называют равномерным прямолинейным.

2. Найти с орость и ус орение точ и, движущейся по вадратичному за ону x(t) = pt2 + qt + r.

Ре ш е н и е. Имеем v(t) = x′(t) = 2pt + q, a(t) = v′(t) = 2p,

т.е. ус орение при движении по вадратичному за ону является постоянным.

Можно до азать и обратное утверждение: если при прямолинейном движении точ и ус орение постоянно, то движение

происходит по вадратичному за ону x(t) = pt2 + qt + r, деоэффициент при t2 численно равен половине ус орения, т. е. p = a/2.

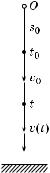
3. Пусть тело свободно падает под действием силы тяжести. Известно, что это движение происходит с постоянным ус орением g — ус орением свободно-о падения. То да пройденное телом расстояние является вадратичной фун цией времени:

причем с орость и ус орение в момент t определя-

ются соотношениями v(t) = s′(t) = gt + v0 и a(t) = v′(t) = = g. При t = 0 из этих соотношений находим s = s0, а

v = v0. Отсюда становится понятным смысл постоянных s0 и v0: это — начальное положение и начальная

Рис. 180 с орость точ и (рис. 180).

410