
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf
$) Область определения фун ции задается системой неравенств
|
sin x l 0, |
|
|
|
2πk m x m π + 2πk, |
|
|||
|
|
|
|
|
|||||
|
|
или |
|
π |
π |
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
|
cos x l 0, |
|
–-- |
+ 2πk m x m -- |
+ 2πk, |
||||
|
π |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
от уда x Ý [2πk; -- + 2πk], k Ý Z. |
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
К упражнению 12а |
|
|
|
|
|
|
|||
1. Имеем y = cos |
2 |
x |
|
1 + cos2x |
|
|
|||
|
= --------------------------- . |
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
2. Та а фун ция cos 2x имеет период π, то и данная фун ция имеет тот же период π.
К упражнению 12
1. Пусть T— период данной фун ции; то$да справедливо тождество
sin3 (x + T) = sin3 x, или sin3 (x + T) – sin3 x = 0. |
(1) |
2. Разложив левую часть уравнения (1) по формуле разности у- бов, получим
sin3 (x + T) – sin3 x = (sin (x + T) – sin x) ×
×(sin2 (x + T) + sin (x + T) sin x + sin2 x) = 0.
3.Упростим второй множитель в уравнении (2):
sin2 (x + T) + sin (x + T) sin x + sin2 x =
= sin x + T |
1 |
sin x |
2 |
3 |
sin2 x. |
||
|
|||||||
+ -- |
|
+ -- |
|||||
|
|
|
2 |
|
|
4 |
|
(2)
(3)
4. Та а выражение (3) неотрицательно, т. е. оно тождественно не равно нулю, то из равенства (2) следует, что должно выполняться тождество
T |
|
T |
|
= 0. |
sin (x + T) – sin x = 0, или 2 sin --- |
cos x + --- |
|||
2 |
|
2 |
|
|
3.Выражение cos x + T тождественно не равно нулю, поэтому
-2--
sin T = 0. Наименьшее положительное значение T, при отором это
---
2
равенство справедливо, есть 2π. Ита , 2π — период данной фун ции.
301
К упражнению 13а
1. Та а y l 4, то 6 y – 4 − 0; то$да систему можно переписать та :
y – 4 − 0; то$да систему можно переписать та :
|
x + y – 3 = 0, |
(1) |
|
|
|||
|
x3 + x2y = 12. |
||
|
|
||
2. Решим систему (1): |
|
||
|
x + y = 3, |
|
|
|
|
||
|
x2(x + y) = 12, |
|
|
|
|
||
или |
|
||
|
|
x + y = 3, |
(2) |
|
|
||
|
|
3x2 = 12. |
|
|
|
|
|
3.Решениями системы (2) являются две пары чисел: x1 = 2, y1 = 1
иx2 = –2, y2 = 5.
4.Но y l 4, поэтому решение данной системы есть единственная
пара чисел: x = –2, y = 5. Ответ: –2.
302

Т е м а 16
À
Свойства функции y = sin x и ее график.
Функция y = arcsin x и ее график. Решение уравнения sin x = a. Свойства функции y = cos x и ее график.
Функция y = arccos x и ее график. Решение уравнения cos x = a. Свойства функции y = tg x и ее график.
Функция y = arctg x и ее график. Решение уравнения tg x = a. Свойства функции y = ctg x и ее график.
Функция y = arcctg x и ее график. Решение уравнения ctg x = a. Некоторые соотношения для аркфункций
Теоретичес ие сведения
1. Свойства функции y = sin x и ее график
1°. Отметим основные свойства фун ции y = sin x:
а) область определения — вся числовая прямая, т. е. D(sin) = = R;
б) множество значений — отрезо [–1; 1], т. е. E(sin) = [–1; 1]; значит, синус — фун ция о раниченная;
в) фун ция нечетная: sin (–x) = –sin x при всех x Ý R;
) фун ция периодичес ая с наименьшим положительным периодом 2π, т. е. sin (x + 2π) = sin x при всех x Ý R;
д) sin x = 0 при x = πk, де k Ý Z;
е) sin x > 0 при всех x Ý (2πk; π + 2πk), k Ý Z;
ж) sin x < 0 при всех x Ý (π + 2πk; 2π + 2πk), k Ý Z;
|
|
з) фун ция возрастает от –1 до 1 в промежут ах |
|
|
|
π |
+ 2πk; |
||||
|
|
|
|||||||||
|
|
|
|
– -- |
|||||||
|
|
|
|
|
|
|
|
2 |
|
||
π |
|
|
|
|
|
|
|
|
|
|
|
+ 2πk |
|
, k Ý Z; |
|
|
|
|
|
||||
-- |
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
и) фун ция убывает от 1 до –1 в промежут ах |
|
|
|
π |
+ 2πk; |
||||
|
|
|
|
|
|||||||
|
|
|
-- |
||||||||
|
|
|
|
|
|
|
|
2 |
|
||
3π |
+ 2πk |
|
, k Ý Z; |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
------ |
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
303

) фун ция принимает наибольшее значение, равное 1, в точ-
ах x = π + 2πk, k Ý Z;
--
2
л) фун ция принимает наименьшее значение, равное –1,
Рис. 147 3π
в точ ах x = ------ + 2πk, k Ý Z.
2
2°. Все перечисленные свойства синуса позволяют построить е о рафи на промежут е [–π; π], т. е. на промежут е, длинаоторо о равна периоду фун ции (рис. 147).
Рис. 148
3°. Та а фун ция y = sin x имеет период 2π, то ее рафи переходит в себя при параллельном переносе r (2π; 0). Поэтомурафи фун ции y = sin x на [–π + 2πk; π + 2πk] получается израфи а, изображенно о на рис. 147, с помощью параллельно-о переноса r (2πk; 0), k Ý Z (рис. 148).
2. Функция y = arcsin x и ее график
1 |
° |
. Фун ция y = sin x на отрез е |
π |
π |
|
возрастает и при- |
|
–-- |
; -- |
|
|||
|
|
|
2 |
2 |
|
|
нимает все значения из отрез а [–1; 1] (см. рис. 147). Поэтому
фун ция y = sin x на отрез е |
|
π |
π |
|
обратима, т. е. имеет об- |
|
|
||||
– -- |
; -- |
|
|||
|
|
2 |
2 |
|
|
ратную фун цию, оторую называют ар син сом и обозначают y = arcsin x. Геометричес и arcsin x означает величину у ла
(ду и), за люченно о в промежут е |
|
π |
; |
π |
|
, синус оторо о |
– -- |
-- |
|
||||
|
|
2 |
|
2 |
|
|
равен x.
304

2°. Графи фун ции y = arcsin x изображен на рис. 149. Этот рафи симметричен рафи у фун ции y = sin x, x Ý
Ý – π ;
--
2
π |
, относительно прямой y = x. |
-- |
|
2 |
|
3°. Отметим свойства фун ции y = |
||
= arcsin x: |
|
|
а) D(arcsin) = [–1; 1]; |
|
|
π |
π |
; |
б) E(arcsin) = –-- |
; -- |
|
2 |
2 |
|
в) фун ция нечетная, т. е. arcsin (–x) = |
|
Рис. 149 |
||||||
= –arcsin x; |
|
|
|
|
|
|
|
|
) фун ция возрастающая. |
|
|
|
|
||||
Пример. Вычислить: |
|
|
|
|
||||
а) arcsin |
|
3 |
|
2 |
; б) tg |
|
1 |
. |
|
–------- |
|
+ arcsin ------ |
|
arcsin -- |
|||
|
2 |
2 |
|
2 |
|
|||
Р е ш е н и е. Имеем:
|
а) arcsin |
|
|
3 |
|
2 |
3 |
2 |
π |
|||
|
|
–------- |
|
+ arcsin ------ |
= –arcsin ------- + arcsin |
------ |
= –-- + |
|||||
|
|
|
|
|
2 |
|
2 |
2 |
2 |
3 |
||
π |
|
π |
|
|
|
|
|
|
|
|
|
|
+ -- |
= – ------ ; |
|
|
|
|
|
|
|
|
|
||
4 |
12 |
|
|
|
|
|
|
|
|
|
||
|
б) tg |
|
|
|
|
1 |
π |
3 |
|
|
|
|
|
|
arcsin -- |
|
= tg -- |
= ------- . |
|
|
|||||
|
|
|
|
|
2 |
6 |
3 |
|
|
|
||
3. Решение уравнения sin x = a |
|
|
|
|||||||||
|
1°. Формула орней уравнения sin x = a ( де |a| m 1) имеет вид |
|||||||||||
|
|
|
|
|
|
x = (–1)k arcsin a + πk, k Ý Z. |
|
|
||||
|
2°. Частные случаи: |
|
|
|
|
|||||||
|
а) sin x = 0 _ x = πk, k Ý Z; |
|
|
|
||||||||
|
б) sin x = 1 |
|
|
π |
|
|
|
|
||||
|
_ x = -- + 2πk, k Ý Z; |
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
π |
+ 2πk, k Ý Z. |
|
|
|
|
в) sin x = –1 _ x = –-- |
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3°. Формула орней уравнения sin2 x = a ( де a m 1) имеет |
|||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = äarcsin |
a + πk, k Ý Z. |
|
|
||
305
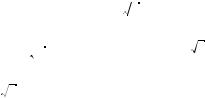
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
Пример. Решить уравнение 2 sin 4-- |
+ x + |
3 = 0. |
|
|||||||||||||||||
Р е ш е н и е. 2 sin |
π |
+ x |
|
+ |
3 = 0 |
_ sin |
π |
+ x |
|
3 |
_ |
|||||||||
-- |
|
-- |
|
= –------- |
||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
2 |
|
||
π |
|
|
|
|
k |
arcsin |
|
|
3 |
+ πk _ |
π |
|
|
|
|
|
||||
_ -- + x = (–1) |
|
|
–------- |
|
-- + x = |
|
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
||
= (–1) |
k |
π |
+ |
|
|
|
|
|
|
|
k + 1 π |
π |
+ πk, k Ý Z. |
|
|
|
||||
|
–-- |
|
πk _ x = (–1) |
-- – -- |
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
||
4. Свойства функции y = cos x и ее график
1°. Отметим основные свойства фун ции y = cos x:
а) область определения — вся числовая прямая, т. е. D(cos) = = R;
б) множество значений — отрезо [–1; 1], т. е. E(cos) = = [–1; 1]; значит, осинус — фун ция о раниченная;
в) фун ция четная: cos (–x) = cos x при всех x Ý R;
) фун ция периодичес ая с наименьшим положительным периодом 2π, т. е. cos (x + 2π) = cos x при всех x Ý R;
д) cos x = 0 при x = π + πk, k Ý Z;
--
2
е) cos x > 0 при всех x Ý |
|
π |
π |
+ 2πk |
|
, k Ý Z; |
||
|
–-- |
+ 2πk; -- |
|
|||||
|
2 |
2 |
|
|
|
|||
ж) cos x < 0 при всех x Ý |
π |
3π |
|
|
|
, k Ý Z; |
||
-- |
+ 2πk; ------ + 2πk |
|
||||||
|
|
2 |
2 |
|
|
|
||
з) фун ция убывает от 1 до –1 в промежут ах [2πk; π + 2πk], k Ý Z;
и) фун ция возрастает от –1 до 1 в промежут ах [–π + 2πk; 2πk], k Ý Z;
) фун ция принимает наибольшее значение, равное 1, в точ-ах x = 2πk, k Ý Z;
л) фун ция принимает наименьшее значение, равное –1, в точ ах x = π + 2πk, k Ý Z.
2°. Все перечисленные свойства осинуса позволяют построить е о рафи на промежут е [–π; π], т. е. на промежут е, длина оторо о равна периоду фун ции (рис. 150).
306
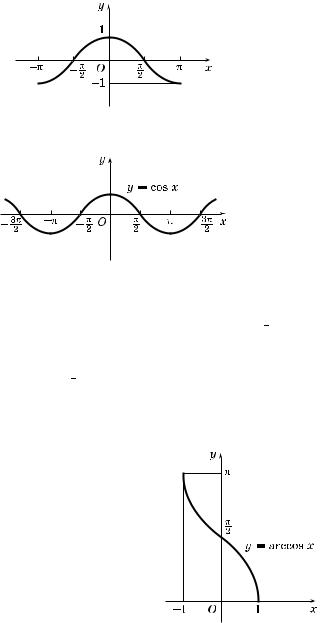
Рис. 150
Рис. 151
3°. В силу то о что период фун ции y = cos x равен 2π, еерафи переходит в себя при параллельном переносе r (2π; 0). Следовательно, рафи фун ции y = cos x на [–π + 2πk; π + 2πk] получается из рафи а, изображенно о на рис. 150, с помощью параллельно о переноса r (2πk; 0), k Ý Z (рис. 151).
5. Функция y = arccos x и ее график |
|
1°. Фун ция y = cos x на отрез е |
|
[0; π] убывает и принимает все значе- |
|
ния из отрез а [–1; 1] (см. рис. 150). |
|
Поэтому фун ция y = cos x на от- |
|
рез е [0; π] обратима, т. е. имеет об- |
|
ратную фун цию, оторую называ- |
|
ют ар осин сом и обозначают y = |
|
= arccos x. Геометричес и arccos x |
|
означает величину у ла (ду и), за- |
|
люченно о в промежут е [0; π], |
|
осинус оторо о равен x. |
|
2°. Графи фун ции y = arccos x |
|
изображен на рис. 152. Этот рафи |
Рис. 152 |
307

симметричен рафи у фун ции y = = cos x, x Ý [0; π], относительно прямой y = x.
3°. Отметим свойства фун ции y = arccos x: а) D(arccos) = [–1; 1];
б) E(arccos) = [0; π];
в) фун ция убывающая;
) arccos (–x) = π – arccos x.
|
3π |
|
|
|
|
2 |
|
Пример. Вычислить ctg --2---- |
– arccos |
–--- |
2--- |
. |
|||
3π |
|
|
|
2 |
|
|
|
Р е ш е н и е. ctg --2---- |
– arccos |
–--- |
2--- |
= |
|
|
|
= ctg 3---- |
π-- |
– |
π – arccos --- |
-- |
2- |
= ctg 3----π-- |
– |
π – -π- |
= |
||
2 |
|
|
|
|
2 |
2 |
|
4 |
|
||
3 |
π |
|
3π |
|
3π |
|
|
|
|
|
|
= ctg --2---- |
– |
--4---- |
= ctg |
--4---- |
|
= –1. |
|
|
|
||
6. Решение уравнения cos x = a
1°. Формула орней уравнения cos x = a ( де |a| m 1) имеет
вид
x = äarccos a + 2πk, k Ý Z.
2°. Частные случаи:
а) cos x = 0 _ x = π + πk, k Ý Z;
--
2
б) cos x = 1 _ x = 2πk, k Ý Z;
в) cos x = –1 _ x = π + 2πk, k Ý Z.
3°. Формула орней уравнения cos2 x = a ( де a m 1) имеет
вид
x = äarccos 
 a + πk, k Ý Z.
a + πk, k Ý Z.
Пример. Решить уравнение
cos 2 x – 1 – 1 = 0.
-3- -2-
308
Р е ш е н и е. cos |
2 |
1 |
|
= 1 |
2 |
1 |
= 2πk _ |
-- x – -- |
|
_ -- x – -- |
|||||
|
3 |
2 |
|
3 |
2 |
|
|
2 |
1 |
3 |
+ 3πk, k Ý Z. |
_ -- x = -- |
+ 2πk _ x = -- |
||
3 |
2 |
4 |
|
7. Свойства функции y = tg x и ее график
1°. Отметим основные свойства фун ции y = tg x:
а) область определения — множество всех действительных
чисел, роме чисел вида x = π + πk, k Ý Z;
--
2
б) множество значений — вся числовая прямая, т. е. E(tg) = = R; та им образом, тан енс — фун ция нео раниченная;
в) фун ция нечетная: tg (–x) = –tg x при всех x Ý D(tg);
) фун ция периодичес ая с наименьшим положительным периодом π, т. е. tg (x + π) = tg x при всех x Ý D(tg);
д) tg x = 0 при x = πk, k Ý Z;
е) tg x > 0 при всех x Ý (πk; π + πk), k Ý Z;
--
2
|
|
|
ж) tg x < 0 при всех x Ý |
|
π |
|
, k Ý Z; |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
–-- + πk; πk |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
з) фун ция возрастает в аждом промежут е |
|
π |
+ πk; |
||||||||||||||||||||
|
|
|
|
– -- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
π |
+ πk |
|
, k Ý Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2°. Все перечисленные свойства тан- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
енса позволяют построить е о рафи |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
на промежут е |
|
π |
π |
, т. е. на проме- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
– -- |
, -- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жут е, длина оторо о равна периоду |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
фун ции (рис. 153). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3°. В силу то о что период фун - |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ции y = tg x равен π, ее рафи перехо- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
дит в себя при параллельном переносе |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
(π; 0). Поэтому рафи фун ции y = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= tg x на |
|
π |
|
|
π |
|
|
получается |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
–-- + πk; |
-- + |
πk- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
Рис. 153 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
309

Рис. 154
из рафи а, изображенно о на рис. 153, с помощью параллельно о переноса r (πk; 0), k Ý Z (рис. 154).
8. Функция y = arctg x и ее график
1 |
° |
|
π |
π |
тан енс возрастает (см. рис. 154) |
. На промежут е |
|
–-- |
; -- - |
||
|
|
2 |
2 |
|
и принимает все числовые значения, т. е. E(tg) = (–×; +×).
Поэтому фун ция y = tg x на промежут е |
|
π |
; |
π |
обратима, |
|
|
–-- |
-- - |
|
|||
|
2 |
|
2 |
|
||
т. е. имеет обратную фун цию, оторую называют ар тан енсом и обозначают y = arctg x. Геометричес и arctg x означает
величину у ла (ду и), за люченно о в промежут е |
|
π |
; |
π |
, |
|
|
– -- |
-- |
- |
|||
|
2 |
|
2 |
|
|
|
тан енс оторо о равен x.
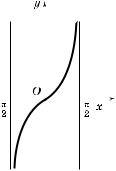
2°. Графи фун ции y = arctg x изображен на рис. 155. Этот рафи симметричен рафи у фун ции y = tg x,
x Ý |
|
π |
π |
|
|
|
|
|
–-- ; |
-- - , относительно прямой |
|||||
|
2 |
2 |
|
|
|
|
|
y = x. |
|
|
|
|
|
|
|
3°. Отметим свойства фун ции y = |
|||||||
= arctg x: |
|
|
|
|
|
||
а) D(arctg) = (–×; +×); |
|||||||
б) E(arctg) = |
|
π |
π |
||||
|
– -- |
; -- |
- ; |
||||
Рис. 155 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
310
