
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf









2 π |
+ sin |
π |
– 1 = 0. В ответе у ажите на- |
|||
5. Решите уравнение 2cos -- |
x-- |
|||||
x |
|
|
|
|
|
|
ибольшее решение на интервале |
|
1 |
; |
1 |
. |
|
-- |
2-- |
|
||||
|
|
4 |
|
|
|
|
6. |
Решите неравенство |
x2 – x – 2 (2x + 24 – x – 10) m 0. В ответе |
||||||||||
у ажите наименьшее решение. |
|
|
|
|
|
|||||||
7. |
Найдите сумму орней уравнения log |
2 |
36 |
– 3 = log |
6 |
|||||||
|
------ |
----- . |
||||||||||
|
|
|
|
|
|
|
|
6 |
x |
|
6 |
x2 |
8. |
Решите неравенство ----- |
3-----–-----2----x-----+------6----x-----–-----5-- > 2. В ответе у |
ажите на- |
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
ибольшее целое решение. |
|
|
|
|
|
|
||||||
9. |
Найдите наименьшее значение фун ции y = ----2-–------2----x-----–---- |
-----1-----–-----2----x-- на |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 – 2x |
|
|
|
–3 ; |
3 |
|
|
|
|
|
|
|
|
|
отрез |
е |
|
|
. |
|
|
|
|
|
|
||
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
10. Конус вписан в шар. Найдите отношение площади поверхно- |
||||||||||||
сти шара |
площади основания онуса, если высота |
онуса равна диа- |
||||||||||
метру е,о основания. |
|
|
|
|
|
|
||||||
Ва р и а н т XVIII
1.Сумма трех чисел, составляющих убывающую ,еометричес ую про,рессию, равна 63. Если сумму перво,о и третье,о чисел разделить на второе, то в частном получится 4, а в остат е 3. Найдите знаменатель про,рессии.
2. При а их значениях a орни x1 и x2 уравнения
9x – (2a + 6)3x + a2 + 6a = 0
удовлетворяют условию x1 < 2 < x2? В ответе у ажите сумму целых значений a.
3.Найдите sin4 x + cos4 x, если sin x + cos x = 1,2.
4.Разность оснований равнобедренной трапеции равна 12, а радиус вписанной в нее о ружности равен 4. Найдите площадь трапеции.
5. |
Решите уравнение 2sin2 |
π |
– cos |
π |
– 1 = 0. В ответе у ажите на- |
|
-- |
-- |
|||||
|
|
x |
|
|
x |
|
ибольшее решение на интервале |
1 |
3 |
|
. |
||
-- |
; -- |
|||||
|
|
|
4 |
4 |
|
|
6. |
Решите неравенство |
|
|
|
|
|

 – x2 + 4x – 3 (3x + 36 – x – 90) l 0. В ответе у ажите наибольшее решение.
– x2 + 4x – 3 (3x + 36 – x – 90) l 0. В ответе у ажите наибольшее решение.
520

 x
x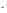
 x
x y – 4x > 4,
y – 4x > 4, y = a(x + 0,5)
y = a(x + 0,5)
 3 , а
3 , а x = y
x = y
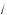 3 . Найдите расстояние между центрами вписанно,о и описанно,о шаров.
3 . Найдите расстояние между центрами вписанно,о и описанно,о шаров.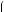 sin x + sin y = 1,
sin x + sin y = 1,  cos x – cos y =
cos x – cos y = 
 3 .
3 .
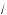 5 , а площадь бо овой ,рани в 3 раза больше площади основания. Найдите объем пирамиды.
5 , а площадь бо овой ,рани в 3 раза больше площади основания. Найдите объем пирамиды. log
log
 log
log log
log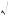 log
log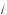 45 – x +
45 – x + 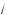 20 + x = 5.
20 + x = 5.
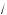 3 , а высота пирамиды равна
3 , а высота пирамиды равна 
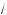 26 . Точ а D лежит на бо овом ребре SC и делит е,о в отношении 2 : 1, считая от вершины S. Найдите площадь сечения ABD.
26 . Точ а D лежит на бо овом ребре SC и делит е,о в отношении 2 : 1, считая от вершины S. Найдите площадь сечения ABD. 50 + x –
50 + x –  x – 22 = 6.
x – 22 = 6.
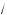 2 , а бо овое ребро равно 3
2 , а бо овое ребро равно 3
 7 . Точ а E лежит на боовом ребре SC и делит е,о в отношении 1 : 2, считая от вершины S.
7 . Точ а E лежит на боовом ребре SC и делит е,о в отношении 1 : 2, считая от вершины S.