Готовимся к экзамену по математике_Крамор В.С_2008 -544с

7. Одна о из найденных значений надо ис лючить те, при оторых

знаменатель данной дроби обращается в нуль, т. е. значения x = π + πk,

--

2

kÝ Z.

8.Из рис. 168, а и б видно, что данное уравнение не имеет решений.

К упражнению 2б

вОДЗ числа « рести ами» на единичной о ружности (рис. 169, а).

2.Приравняв нулю числитель дроби, получим уравнение cos 3x = 0,

4. Теперь из множества отмеченных точе нужно оставить те, о- торые входят в ОДЗ: это P0, P2, P3 и P5 (рис. 169, б).

5. Ита , получаем ответ: x = äπ + πk, k Ý Z.

--

6

Рис. 169

371

К упражнению 3а

1. Требуется решить уравнение

Отметим следующее:

а) левая часть уравнения (1) состоит толь о из ал$ебраичес ой суммы, причем аждое сла$аемое этой суммы является произведением числово$о множителя и двух фун ций синуса или осинуса одно$о и то$о же ар$умента;

б) сумма по азателей степеней синуса и осинуса в аждом сла- $аемом одна и та же (в данном уравнении она равна 2);

в) свободный член в уравнении (1) отсутствует, т. е. он равен нулю; $) та ое уравнение называют однородным относительно фун ций

sin x и cos x, а 2 — это степень е$о однородности.

2. Значения ар$умента, при оторых cos x = 0, не являются решениями уравнения (1), та а если cos x = 0, то должно выполняться равенство –3sin2 x = 0, а осинус и синус одно$о и то$о же ар$умента не мо$ут одновременно быть равными нулю. Поэтому обе части уравнения (1) можно разделить на cos2 x или на sin2 x, причем получится уравнение, равносильное уравнению (1).

3. Разделив все члены уравнения (1) на cos2 x − 0, получим

К упражнению 3в

1.Данное уравнение не является однородным три$онометричес им уравнением, та а в нем есть отличный от нуля свободный член, равный 2.

2.Очевидно, что данное уравнение ле$ о свести однородному уравнению второй степени, если свободный член умножить на выра-

жение sin2 x + cos2 x, равное 1.

3. То$да придем однородному три$онометричес ому уравнению

равносильному данному. После упрощений получим cos2 x – cos x sin x – 2 sin2 x = 0,

т. е. однородное уравнение второй степени относительно sin x и cos x.

372

4. Разделив аждый е$о член на cos2 x − 0, имеем

1 – tg x – 2 tg2 x = 0. (2) 5. Решим уравнение (2):

К упражнению 3д

1.Это однородное три$онометричес ое уравнение второй степени.

2.Чтобы решить е$о, разложим левую часть уравнения на множи-

тели:

cos x(3 sin x – 5 cos x) = 0.

3.Та им образом, нужно решить простейшее три$онометричес ое уравнение cos x = 0 и однородное уравнение первой степени 3 sin x –

–5 cos x = 0.

4.Имеем

3 tg x – 5 = 0,

от уда x = arctg 5 + πk, k Ý Z. Та им образом, те значения x, при о-

--

3

торых cos x = 0, о азались потерянными. Чтобы не произошло потериорней, подобные уравнения следует решать разложением на множители, а это было сделано выше.

К упражнению 4а

1. Применяя формулы преобразования произведения три$онометричес их фун ций в сумму, запишем данное уравнение в виде

373

3. Из уравнения sin 5πx = 0 следует, что 5πx = πk, т. е. x =

k Ý Z. Теперь воспользуемся тем, что орни уравнения принадлежат

отрез у [3; 4], т. е. 3 m k m 4, или 15 m k m 20. Этому неравенству удов-

--

5

летворяют 6 орней.

4. Из уравнения cos 8πx = 0 следует, что 8πx = + πk, от уда

Этому неравенству удовлетворяют 8 орней. Ответ: 14 орней.

К упражнению 6а

1. Используя формулу приведения, перепишем данное уравнение та :

Можно по азать, что при этих значениях x знаменатель дроби (2) не обращается в нуль, т. е. что равенство (3) задает серию орней исходно$о уравнения.

4. Далее мы должны найти сумму 48 положительных орней уравнения. Для это$о совсем не обязательно придавать k значения от 0 до 47 и непосредственно с ладывать 48 чисел.

К упражнению 7а

1. Пере$руппируем члены данно$о уравнения следующим образом:

2.Разложим на множители левую часть уравнения (1): 35(1 – 2 sin2 2x – sin 2x) = –35(sin 2x + 1)(2 sin 2x – 1).

3.Разложим на множители правую часть уравнения (1): 12(2 sin 2x cos 2x – cos 2x) = 12 cos 2x(2 sin 2x – 1).

4.То$да уравнение (1) примет вид

–35(sin 2x + 1)(2 sin 2x – 1) – 12 cos 2x(2 sin 2x – 1) = 0,

или

375

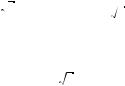
б) 35(sin 2x + 1) + 12 cos 2x = 0, или 35 sin 2x + 12 cos 2x + 35 = 0; пола$ая tg x = t, получим

3.Решив уравнение (2), получим

x – y = (–1)karcsin (2p – sin q) + πk, k Ý Z, $де |2p – sin q| m 1.

376

4. Остается решить систему

x + y = q,

x – y = (–1)karcsin (2p – sin q) + πk,

от уда находим

377

К упражнению 8

1. Находим ОДЗ системы:

К упражнению 9а

1. Преобразуем данное выражение с помощью введения вспомо$а- тельно$о у$ла. Напомним формулу, содержащую вспомо$ательный у$ол:

378

2. В рассматриваемом случае имеем a = 3, b = 4, 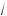a2 + b2 = 5,

3.То$да данное выражение запишется следующим образом: 5(cos α sin x + sin α cos x) = 5sin (x + α).

4.Выражение 5sin (x + α) принимает наибольшее значение, равное 5, и наименьшее значение, равное –5.

К упражнению 10и

1. После преобразований данное неравенство примет вид

2. Та а вадратный трехчлен 2y2 + 7y + 3 ($де y = sin x) имеет

множители, получим

4. Для решения неравенства (3) воспользуемся числовой о ружностью (рис. 170). Решением неравенства являются все числа, удовлетворяющие услови-

379

К упражнению 10л

1. Найдем ОДЗ неравенства:

2. Преобразуем данное неравенство:

2 + 3 sin2x l 0; (2 + 3sin 2x) sin 2x l 0.

------------------------------

sin2x

380