Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Готовимся к экзамену по математике_Крамор В.С_2008 -544с

.pdf

Скачиваний:

484

Добавлен:

26.03.2016

Размер:

7.3 Mб

Скачать

☆

<<< < Предыдущая 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 4950 / 5550 51 52 53 54 55 > Следующая >>>

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение инте,- рала.

2. Что означают в записи

b	b
∫ f(x) dx: а) числа a и b; б) зна	∫ ;
a	a

в) f(x); ,) x; д) f(x) dx? Может ли быть a = b; a > b?

3.Зависит ли приращение F(b) – F(a) от выбора первообразной?

4.Ка ое со ращенное обозначение принято для приращения первообразной F(b) – F(a)?

5.Вычислите:

	2
а)	∫ x2 dx;
	–1
	π
б)	∫	sin x dx;
	0
	π/4
в)	∫	dx
в)		--------------- .
		cos2 x
	0

6. Вычислите инте,рал:

	4	x2				3		5
а)	∫			–		3	+	5	dx;
а)				–		--	+	-----------	dx;
						4		x x
	0,25
	–2π			dx
б) ∫				dx
б) ∫		------------------------------- ;
	–π	sin	2		π		x
	–π	sin			--	+ --
					6		3
	–4
в) ∫		x				dx.
в) ∫		---------------------				dx.
	0	1 – 2x
	0

7. В чем за лючается ,еометричес ий смысл инте,рала?

8.В чем за лючается разница между понятиями «перемещение точ и» и «путь, пройденный точ ой»?

9.Пружина растя,ивается на 1 см под действием силы 10 Н. Ка ую работу надо произвести, чтобы растянуть пружину на 4 см?

УПРАЖНЕНИЯ

1. Вычислите инте рал:

а)

д)

2		π/2
∫	x4 dx; б)	∫
–1		0
2	dx
∫	dx	; е)
	-------------------------	; е)
	(2x + 1)2
1

			3
cos x dx; в) ∫				x3 dx;
			1		10 dx
π		x			10 dx
∫	3cos	2	dx; ж)		∫	x2
	3cos	--	dx; ж)			------
0					1

	π/4	dx
)	∫	dx	;
)		---------------	;
		cos2 x
	0

π/2

;з) ∫ sin 2x dx.

π/4

2. До ажите справедливость равенства:

π/4	d x 2		1
а) ∫	d x 2	=	∫
	cos x

π/2

в) ∫ cos x dx =

π/3		1/4	dx
dx; б) ∫	sin x dx =	∫		;
			-------
0		1/16	x

3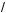3 1 2

∫ x2 dx; ) ∫ (2x + 1) dx = ∫ (x3 – 1) dx.

0 0 0

491

3. Вычислите площадь фи уры, о раниченной линиями: а) y = x4; y = 1; б) y = x2 – 4x + 4; y = 0, x = 4;

в) y = x2 – 4x + 5, y = 5; ) y = –x2 – 4x; y = 0, x = –3, x = –1; д) y = –x2 – 4x; y = 1, x = –3, x = –1; е) y = x3; y = 8; x = 1;

ж) y = 2 – x3, y = 1; x = –1, x = 1; з) y = 1 ; y = x; x = 2;

-----

и) y = 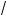x , y = x; ) y = –(x –1)3, y = 0, x

3π 3π

л) y = 3 sin(x + ------ ), y = 0, x = –------ , x =

4 4

= 0;

3π

------ .

4. Вычислите площадь фи уры, о раниченной линиями:

а) y = x2 – 4x + 4, y = 4 – x2; б) y = x2 – 2x + 2; y = –x2 + 6x + 2; в) y = x2, y = 2x – x2; ) y = x2; y = x3.

5. Вычислите площадь фи уры, о раниченной рафи ом фун ции:

а) y = 8x – 2x2, асательной этой параболе в ее вершине и прямой x = 0;

б) y = 8 – 1 x2, асательной нему в точ е с абсциссой x =

= –2 и прямой x0 = 1.

Задания для повторения

6.Для составления бу етов за упили 60 роз и возди . Если бы роз за упили в 2 раза больше, то общее число цветов было бы меньше 88, а если бы за упили в 2 раза больше возди , то общее число цветов было бы меньше 94. С оль о роз было за уплено?

7.На из отовление 20 порций перво о блюда расходуется 0,5 мяса и 1 риса, а на из отовление одной порции второ-о блюда — 100 мяса и 150 риса. Требуется из отовить вторых блюд в 1,5 раза больше, чем первых, при этом израсходовать не менее 11,1 мяса и не более 17,7 риса. С оль о все-о порций блюд было из отовлено?

8.Найдите площадь фи уры, задаваемой на плос ости множеством решений системы неравенств:

|x2 + y2 + 2x – 6y + 5| m 1, а) 3x – y + 6 l 0,

x + 3y – 8 m 0;

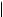|x2 + y2 – 4x + 2y + 1,5| m 0,5, б) 4x – y – 9 m 0,

x + 4y + 2 m 0.

492

9. При а их значениях a имеет два различных орня уравнение:

а) 4x + 2(a – 2)2x – 3a2 + 8a – 5 = 0;

б) 9x – (4a + 2) · 3x – 5a2 + 34a – 24 = 0? 10. Решите уравнение:

		а) log									2πx		+ sin				πx		+ 1	= 0;
		а) log			πx				sin ----------				+ sin				------		+ 1	= 0;
				sin ------								3					3
					3
		б) log						2			2 cos2		πx		+				x – 2		cos			πx		= 0.
		б) log			πx			2			2 cos2		------		+				x – 2		cos		------			= 0.
				tg	------								3										3
					3
		11. Решите неравенство:
		а) x2 – 8					x		+ 7 > x + 2; б) x2 – 9													x		+ 14 > 1 – x.
		а) x2 – 8					x		+ 7 > x + 2; б) x2 – 9													x		+ 14 > 1 – x.

		О Т В Е Т Ы
		1. а) 6,6; б) 1; в) 20; ,) 1; д)															1	; е) 6; ж) 0,9; з) 0,5. 3. а) 1,6											в. ед.;
		1. а) 6,6; б) 1; в) 20; ,) 1; д)														------		; е) 6; ж) 0,9; з) 0,5. 3. а) 1,6											в. ед.;
																15
б)	16		в. ед.; в)					32			в. ед.;				22				в. ед.;		16						17		в. ед.;
б)	------		в. ед.; в)					------			в. ед.;			,) ------					в. ед.;		д) ------				в. ед.; е) ------				в. ед.;
		3							3							3					3						4
ж) 2			в. ед.;			з) 1					в. ед.;			и)		1			в. ед.;				1		в. ед.;		л) 9		в. ед.
ж) 2			в. ед.;			з) 1					в. ед.;			и)		--			в. ед.;		) --				в. ед.;		л) 9		в. ед.
																6							4
4. а)			8	в. ед.; б)					64		в. ед.; в)					1					1			в. ед. 5. а)			16		в. ед.;
4. а)			--	в. ед.; б)					------		в. ед.; в)					--		в. ед.; ,) ------						в. ед. 5. а)			------		в. ед.;
			3							3						3					12						3
б)	9		в. ед. 6. 27. 7.								160. 8. а)				π		в. ед.; б)				π		в. ед. 9. а) a Ý					1;	3
б)	--		в. ед. 6. 27. 7.								160. 8. а)				--		в. ед.; б)				--		в. ед. 9. а) a Ý					1;	--
	2														2						4								2
		2	5	; б) a Ý						4	5			5	; 6 . 10. а) 2 + 6n, n Ý Z; б) 4 + 6n, n Ý Z.
		--	; --	; б) a Ý						--	; --			--	; 6 . 10. а) 2 + 6n, n Ý Z; б) 4 + 6n, n Ý Z.
		3	3							5	3			3
											3	< x	<	1	; б) –				13
11. а) –× < x m –7, –--												< x	<	--	; б) –				------ < x m2, 7 m x < +×.
											4			4					11

Решения и методичес ие у азания

К упражнению 1а

1.								x5
1.	Для фун ции f(x) = x4 первообразной служит фун ция ----- .
								5
2.	Следовательно, по формуле Ньютона—Лейбница находим
	2			x5	2	25	(–1)5
	∫	x	4	x5	2	25	(–1)5	= 6,6.
	∫	x		dx = -----		= -----	– --------------	= 6,6.
	–1			5	–1	5	5
	–1

493

К упражнению 1б

1.Для фун ции f(x) = cos x первообразной является фун ция sin x.

2.Та им образом, по формуле Ньютона—Лейбница имеем

π/2

∫ cos x dx = sin x π ⁄ 2

К упражнению 1д

1. Для заданной фун ции f(x) =

= sin -- – sin 0 = 1.

1	первообразной является
(---2----x-----+------1----)--2-

1	1
фун ция – --	· ----------------- .
2	2x + 1
2. Значит, со,ласно формуле Ньютона—Лейбница, получаем
2	dx	1	1		2	1	1	1		1
	dx	1	1		2	1	1	1		1
∫	-------------------------	= –--	· -----------------			= –--	--	– --	= ------ .
∫	(2x + 1)2	2	2x + 1		1	2	5	3		15
1
К упражнению 1е
1. Для фун ции		f(x) =	3 cos	x		первообразная				есть фун ция
1. Для фун ции		f(x) =	3 cos	--		первообразная				есть фун ция
				2

6 sin -- .

2. Следовательно, по формуле Ньютона—Лейбница находим

∫

3cos

= 6sin

-- dx

-- – 6sin 0 = 6.

К упражнению 2а

1. Требуется до

азать справедливость равенства

π/4

∫

dx.

(1)

---------------

∫ cos2 x

2. Для фун

первообразная есть фун

ция tg x.

ции f(x) = ---------------

cos2 x

3. Та им образом, в левой части равенства (1) имеем

π/4

∫

= tg x

π ⁄ 4

– tg 0 = 1.

---------------

= tg --

cos2 x

494

4. Вычислим теперь правую часть равенства (1):

1
∫	dx = x	1	= 1 – 0 = 1.
∫	dx = x	1	= 1 – 0 = 1.
		0
0

5. Ита , равенство (1) справедливо.

К упражнению 2б

1. До ажем справедливость равенства

π/3	1/4
∫ sin x dx =	∫	dx
∫ sin x dx =	∫	------- .	(1)
		x

01/16

2.Для фун ции f(x) = sin x первообразная есть фун ция (–cos x).

3.Значит, в левой части равенства (1) имеем

π/3

∫	sin x dx = –cos x					π ⁄ 3					π						1	+ 1 =		1
						π ⁄ 3					π						1			1
								= –cos --					+ cos 0 = –--							-- .
						0					3						2			2
0			1				первообразной является фун													ция 2 x .
			1
4. Для фун ции f(x) = -------
					x
5. Поэтому в правой части равенства (1) имеем
1/4
	∫	dx			= 2			1			–	1		= 2		1	–	1	1
		dx		1/ 4				1				1				1		1	1
		------- = 2 x							--			------				--		--	= -- .
		x		1/16					4			16				2		4	2
1/16
6. Ита , справедливость равенства (1) до															азана.
К упражнению 3а
1. Построив данные линии, полу-
1. Построив данные линии, полу-
чим фи,уру, площадь			оторой нужно
найти (на рис. 241 эта фи,ура заштри-
хована).
2. Пределы инте,рирования най-
дем из равенства x4 = 1, от							уда x			1	=
= –1, x2 = 1.										1
= –1, x2 = 1.
3. Ис омая площадь равна разнос-
ти между площадью прямоу,ольни а
ABCD и площадями двух равных фи-																	Рис. 241

495

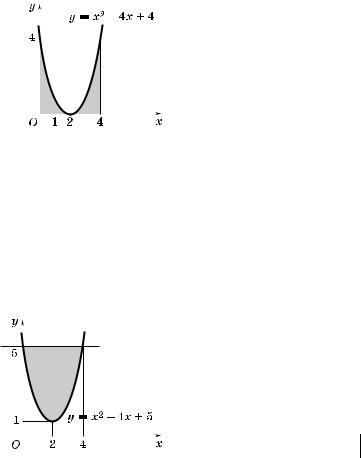
,ур ABO и DCO. В силу симметрии заданной фи,уры относительно оси Oy можно найти половину ис омой площади и результат удвоить. Имеем

	1	1
	∫	dx – ∫		= 2	x	1	x5	1	= 2	1	8	( в. ед.).
						1	x5	1		1	8
S = 2			x4 dx				– -----			1 – --	= --
						0	5	0		5	5
						0		0

К упражнению 3б

1. Фи,ура, площадь

оторой тре-

буется определить, заштрихована на

рис. 242.

2. Найдем ис омую площадь:

S = ∫ (x2 – 4x + 4) dx =

+ 4x

= ----- – 2x2

(

в. ед.).

Рис. 242

------ – 32 + 16 = ------

К упражнению 3в

1. Построим заданные линии и изобразим фи,уру, площадь ото-

рой нужно определить (рис. 243).
		2. Пределы инте,рирования най-
		дем из равенства x2 – 4x + 5 = 5, или
		x2 – 4x = 0, т. е. x		1	= 0, x	2	= 4.
				1		2
		3. Вычислим ис омую площадь:
		4	4
		4	4
		S = ∫ 5 dx – ∫ (x2 – 4x + 5) dx =
		0	0
		4
		= ∫ (5 – x2 + 4x – 5) dx =
		0
		4					x3	4
		4
		= ∫ (4x – x2) dx = 2x2
		= ∫ (4x – x2) dx = 2x2					– -----	=
		0					3	0
		0
		64	=		32
		= 32 – ------	=		------ ( в. ед.).
	Рис. 243	3			3

496

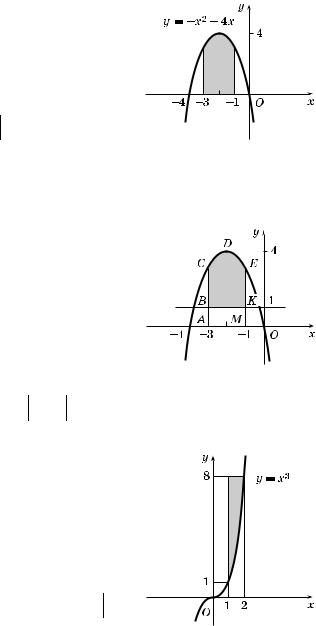
К упражнению 3

1.Фи,ура, площадь оторой требуется найти, заштрихована на рис. 244.

2.Вычислим ис омую площадь:

–1

S = ∫ (–x2 – 4x) dx =

–3

–1

(1)3

– 2(–1)

–

–----- – 2x

= – ----------

–3

–

(–3)3

– 2

–3-

( в. ед.).

–--------------

= ------

К упражнению 3д

1.Изобразим заданные линии и получим фи,уру, площадь оторой нужно найти (эта фи,ура на рис. 245 заштрихована).

2.Ис омая площадь равна разности между площадью риволинейной трапеции ACDEM и площадью прямоу,ольни а ABKM.

3.Та им образом,

–1 –1

S = ∫ (–x2 – 4x) dx – ∫ dx =

–3					–3
= –	x3	– 2x2		–1	–1	=
= –	-----	– 2x2	-		– x-	=
	3			–3	–3
22	+ 1 – 3 =			16	( в. ед.).
= ------	+ 1 – 3 =			------	( в. ед.).
3				3

К упражнению 3е

1.Фи ура, площадь оторой нужно

определить, заштрихована на рис. 246.

2.Чтобы найти верхний предел инте,рирования, решим уравнение

x3 = 8, от уда x = 2. 3. Следовательно,

2	2				x4	2
S = ∫					x4	2
S = ∫	8 dx – ∫ x3 dx = 8x – -----					=
1	1				4	1
1	1
= 16 – 4 – 8 +		1	17	(	в. ед.).
= 16 – 4 – 8 +		--	= ------	(	в. ед.).
		4	4

Рис. 244

Рис. 245

Рис. 246

497

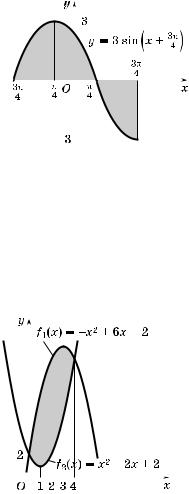
К упражнению 3л

1. Построим ,рафи фун

ции y = 3sin x +

3π

(рис. 247).

------

2. Для фун ции y = 3 sin

3π

одной из первообразных являет-

x + ------

ся фун ция F(x) = –3 cos

3π

+ ------

3. Значит,

S = F(x)-

π/ 4

– F(x)-

3π/4 =

–3π/4

π/4

– F –

3π

------ -

–

3π

– F

------ -

= (–3 cos π + 3 cos 0) –

–

3π

+ 3 cos π-

= 9 (

в. ед.).

Рис. 247

–3 cos ------

К упражнению 4б

1. Построим заданные линии и получим фи,уру, площадь

оторой

требуется определить (на рис. 248 эта фи,ура заштрихована).

2. Для нахождения пределов инте,рирования решим уравнение

x2 – 2x + 2 = –x2 + 6x + 2, или 2x2 – 8x = 0, от уда x					1	= 0, x	2	= 4.
		3. Ис омую площадь находим
		по известной формуле
			b			b
			b			b
		S = ∫ f1(x) dx – ∫ f2(x) dx,
			a			a
		т. е.
		4
		∫ (–x2 + 6x + 2) dx –
		0	4
			4
			– ∫ (x2 – 2x + 2) dx =
		4	0
		4
		= ∫ (–2x2 + 8x) dx =



		0	=	2					4
				2					4
				–-- x3 + 4x2					=
				3					0
				3					0
		2				64	в. ед.).
	Рис. 248	= –--	· 64 + 64 = ------ (				в. ед.).
		3				3

498

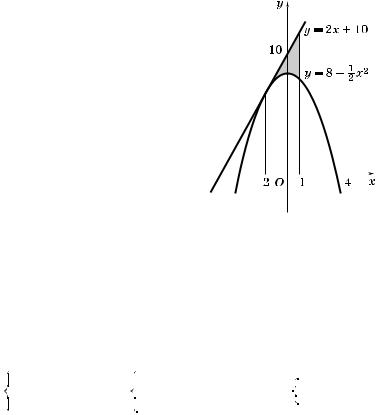
К упражнению 5б

1. Кроме у азанных в условии линий, необходимо найти еще одну —

асательную ,рафи у фун ции f(x) = 8 –				1	в точ	е с абсциссой
асательную ,рафи у фун ции f(x) = 8 –				-- x2	в точ	е с абсциссой
				2
x0 = –2.
2.	Запишем уравнение		асательной в общем виде:
		f(x) – f(x0) = f′(x0)(x – x0).				(1)
3.	Находим:
а) f(x		1
а) f(x		) = f(–2) = 8 – -- (–2)2 = 6;
	0	2
		2
б) f′(x) = –x, от уда			f′(x0) = f′(–2) = 2.
4.	Подставив эти значения в урав-

нение (1), получим уравнение асательной:

f(x) – 6 = 2(x + 2),

или

f(x) = 2x + 10.

5. Построим все эти линии и изобразим фи,уру, площадь оторой требуется определить (на рис. 249 эта фи- ,ура заштрихована).

6. Имеем

	1							1			1		2
	∫							∫			1		2
S =	∫	(2x + 10) dx –						∫	8 –		2	x -		dx =
S =		(2x + 10) dx –							8 –		--	x -		dx =
	–2						–2
= (x2			4	1		–		8x –		x3		4	1	=
			4	1						x3		4	1
			+ 10x)-							----- -		-
				–2						6			–2		Рис. 249
			9		(	в. ед.).									Рис. 249
			9
			= --
			2

К упражнению 6

1.Обозначим ис омое число роз через x, а число ,возди — через y (,де x, y Ý N).

2.Используя условие задачи, составим и решим систему уравнений

x + y = 60,	y = 60 – x,	x < 28,

2x + y < 88, или	2x + 60 – x < 88, или
		x > 26.
x + 2y < 94,	x + 2(60 – x) < 94,

Учитывая, что x — натуральное число, получим x = 27.

499

К упражнению 8а

1. Исходная система неравенств равносильна следующей:

–1 m x2 + 2x + 1 – 1 + y2 – 6y + 9 – 9 + 5 m 1 y m 3x + 6,

1	8	,
y m –--	x + --	,
3	3

или
	4 m (x + 1)2 + (y – 3)2 m 6,		(1)
	4 m (x + 1)2 + (y – 3)2 m 6,		(1)
	y m 3x + 6,		(2)
	1	8	(3)
	1	8
	y m – -- x +	-- .
	3	3
2. Неравенство (1) задает на оординатной плос ости			ольцо

(рис. 250), образованное онцентричес ими о ружностями с общим

центром C(–1; 3) и радиусами r1 = 2 и r2 =			6 .
1	x +	8	перпенди улярны, та а
3. Прямые y = 3x + 6 и y = –--	x +	--	перпенди улярны, та а
3		3

произведение их у,ловых оэффициентов k1k2	= 3(–	1	) = –1, и пересе-
		--
		3

аются в точ е C(–1; 3).

4. Ита , находим площадь фи,уры, заштрихованной на рис. 250:

1	π r	2	– π r	2		1	π	(	в. ед.).
S = --	π r	2	– π r	1	-	= --	(6π – 4π) = --	(	в. ед.).
4		2		1		4	2
						Рис. 250

500

<<< < Предыдущая 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 4950 / 5550 51 52 53 54 55 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.05.2015121.34 Кб8Глава 3.doc
#
31.05.2015262.14 Кб5Глава 4.doc
#
26.03.201634.51 Кб69Голубь задачи.docx
#
31.05.2015102.4 Кб8ГОС.РТ.doc
#
31.05.20151.48 Mб3ГОСТ 91.doc
#
26.03.20167.3 Mб484Готовимся к экзамену по математике_Крамор В.С_2008 -544с.pdf
#
31.05.2015243.71 Кб116грам.стил.doc
#
31.05.201520.85 Кб39гтн25.docx
#
31.05.20153.6 Mб66Деревянко_БС ЭВМ.pdf
#
31.05.20151.34 Mб57дип20.docx
#
31.05.20151.08 Mб95Диплом .doc